分數階Langford系統的穩定性分析

朱香梗，李玉霞2，武 波

(1.山東科技大學 數學與系統科學學院，山東 青島 266590;2.山東科技大學 電氣與自動化工程學院，山東 青島 266590)

分數階微積分是對整數階微積分的推廣，整數階微積分可以看成是分數階微積分的特例，因此研究分數階微積分更具有普遍意義[1]。在描述復雜物理學問題時，與非線性模型相比較，分數階模型的物理意義更清晰，表述更簡潔[2]。分數階控制隨著分數階導數的不同可以增大控制的自由度，從而可獲得更優良的控制性能；另一方面，分數階微積分具有記憶功能，這種記憶功能確保歷史信息對現在和未來的影響，有利于改善控制的品質[3-4]。

三維動力系統在非線性電路、生物網絡以及信息安全等領域有著巨大的應用潛力，現已成為非線性科學理論與應用研究的熱點[5-7]。隨著現代數學研究的不斷發展，分數階系統動力學的研究引起了廣泛關注，產生了一系列重要的研究成果，包括穩定性分析、分岔與混沌等[8-10]。近年來，分數階系統在系統控制、粘彈性阻尼、電解質極化、分形與混沌和機器人等領域得到了廣泛推廣和應用，這一推廣在跨學科領域的應用中表現尤為普遍[11-12]。

Langford系統是Langford W.F.根據Hopf建立的湍流模型演變而來的，研究表明，該系統具有豐富的非線性動力學行為。文獻[13]對Langford系統中的規則運動進行定性分析，研究了Langford系統的混沌特性、Hopf分岔以及極限環的穩定性，并給出了全局分岔圖。Nikolov等[14]給出了Langford系統的第一個Lyapunov值的具體表達式，并首次得到一個混沌解[14]。目前，對于Langford系統的研究結果僅限于整數階，對分數階Langford系統的研究較少。本研究基于Lyapunov穩定性定理，著重分析分數階Langford系統的穩定性，給出系統保持穩定的條件。研究結果將有助于豐富Langford系統的穩定性理論，為進一步討論分數階Langford系統的控制問題提供參考意義。

1 分數階Langford系統的數學模型

分數階微積分有多種定義， 常用的定義有三種，即：Caputo定義、 Grunwald-Letnikov 定義和Riemann-Liouville定義。由于Caputo導數只需根據整數階導數給出的初始條件即可表示實際情況中良好的特性，更適用于工程問題，因此本研究基于Caputo導數定義。

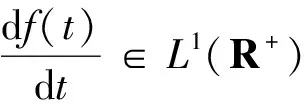
(1)

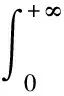
首先引入分數階線性系統的穩定性定理。

引理1[16]對于下面的分數階自治系統：

(2)

其中0<α<1，x∈Rn且A∈Rn×n，如果矩陣A的所有特征值λ滿足|arg(λ)|>απ/2，則系統 (2) 的零解是漸近穩定的。

文獻[17]考慮了如下Langford系統：

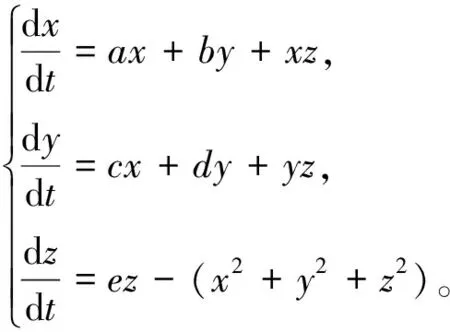
(3)

其中a,b,c,d,e表示系統參數。易見，系統 (3) 具有兩個平衡點O(0,0,0)和E(0,0,e)。

利用分數階Caputo微分定義將上述系統轉化為分數階，得到分數階Langford系統數學模型如下：

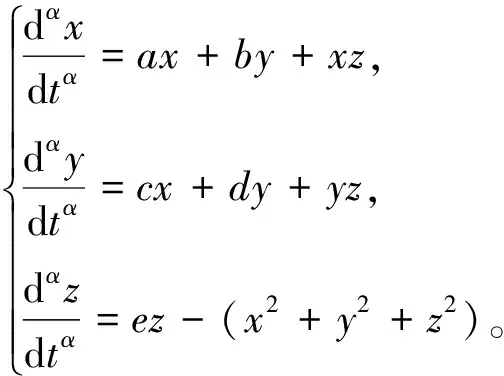
(4)

其中α∈(0,1]。

2 Langford系統在平衡點處的穩定性

2.1 系統在平衡點O(0,0,0)處的穩定性

易見系統 (4) 對應的雅可比矩陣為：

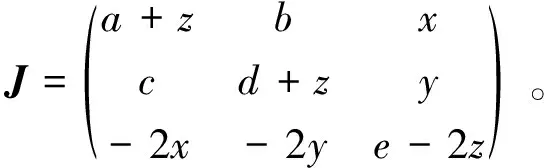
將平衡點O代入，可得此時雅可比矩陣為：

J1對應的特征方程為：

p1(λ)=(λ-e)[λ2-(a+d)λ+(ad-bc)]。

(5)

記

Δ1=(a+d)2-4(ad-bc)。

則特征方程(5)的特征根分別為：

下面，通過討論參數a,b,c,d,e的取值范圍來分析特征方程(5)根的正負性。

引理2對于特征方程(5)，可知：

1) 當Δ1>0且ad-bc≠0時，特征方程(5)的所有根都為實數：

① 如果e>0，ad-bc>0且a+d>0，則特征方程(5)有三個正實根；

② 如果e>0，ad-bc>0且a+d<0，則特征方程(5)有一個正實根，兩個負實根；

③ 如果e>0且ad-bc<0，則特征方程(5)有兩個正實根，一個負實根；

④ 如果e<0，ad-bc>0且a+d>0，則特征方程(5)有兩個正實根，一個負實根；

⑤ 如果e<0，ad-bc>0且a+d<0，則特征方程(5)有三個負實根；

表1 特征方程(5)的根在空間(a,b,c,d,e)中的分布Tab.1 Distribution of roots of Eq.(5) in (a,b,c,d,e)-space

⑥ 如果e<0且ad-bc<0，則特征方程(5)有兩個負實根，一個正實根。

2)當Δ1<0且ad-bc≠0時，特征方程(5)有一個實數根和一對復共軛根：① 如果e>0且a+d>0，則特征方程(5)有一個正實根和一對復共軛根，其中復根的實部均為正數；② 如果e>0且a+d<0，則特征方程(5)有一個正實根和一對復共軛根，其中復根的實部均為負數；③ 如果e<0且a+d>0，則特征方程(5)有一個負實根和一對復共軛根，其中復根的實部均為正數；④ 如果e<0且a+d<0，則特征方程(5)有一個負實根和一對復共軛根，其中復根的實部均為負數。

由引理2可以看出曲線Δ1=0,e=0,ad-bc=0,a+d=0將空間(a,b,c,d,e)分成了如表1中的10個區域。易得：

定理1分數階Langford系統在平衡點O(0,0,0)處的穩定性結論如下：

1) 如果(a,b,c,d,e)∈Ω5∪Ω10，則系統(4)在平衡點O(0,0,0)處對任意的α∈(0,1]都是局部漸近穩定的；

2) 如果(a,b,c,d,e)∈Ω1∪Ω2∪Ω3∪Ω4∪Ω6∪Ω7∪Ω8，則系統(4)在平衡點O(0,0,0)處對任意的α∈(0,1]都是不穩定的；

3) 如果(a,b,c,d,e)∈Ω9且α滿足下面的不等式

(6)

則系統 (4) 在平衡點O(0,0,0)處是局部漸近穩定的；

4) 如果(a,b,c,d,e)∈Ω9且α滿足下面的不等式

(7)

則系統 (4) 在平衡點O(0,0,0)處是不穩定的。

證明：由引理1，易得如下結論

1) 如果(a,b,c,d,e)∈Ω5∪Ω10，則式(5)的所有實特征根和共軛特征根的實部都為負數。這意味著方程 (5) 的所有特征根都在穩定域內。因此，系統(4)在平衡點O(0,0,0)處是局部漸近穩定的。

2) 如果(a,b,c,d,e)∈Ω1∪Ω2∪Ω3∪Ω4∪Ω6∪Ω7∪Ω8，則方程 (5) 至少有一個正實根。因此系統 (4) 在平衡點O(0,0,0)處是不穩定的。

3) 如果(a,b,c,d,e)∈Ω9, 則特征方程(5)有一對具有正實部的復共軛特征根λ2,3以及一個負實根λ1，分別為：

進而有

因此，若滿足式(6)，則系統 (4) 在平衡點O(0,0,0)處是局部漸近穩定的。

4) 由3)中的推論可知，若 滿足式(7)，則系統(4)在平衡點O(0,0,0)處是不穩定的。

2.2 系統在平衡點E(0,0,e)處的穩定性

系統在平衡點E(0,0,e)處的雅可比矩陣為：

J2對應的特征方程為：

p2(λ)=(λ+e)[λ2-(a+d+2e)λ+(a+e)(d+e)-bc]。

(8)

記

Δ2=(a+d+2e)2-4[(a+e)(d+e)-bc],μ0=(a+e)(d+e)-bc。

特征方程 (8) 的特征根分別記為：

下面通過討論參數a,b,c,d,e的取值范圍來分析特征方程(8)的根的特性。

引理3對于特征方程 (8)，有如下結果：

1) 當Δ2>0且μ0≠0時，特征方程(8)的所有特征根都為實數：

① 如果e>0，μ0>0且a+d+2e>0，則特征方程(8)有兩個正實根，一個負實根；

② 如果e>0，μ0>0且a+d+2e<0，則特征方程(8)有三個負實根；

③ 如果e>0，μ0<0，則特征方程(8)有兩個負實根，一個正實根；

④ 如果e<0，μ0>0且a+d+2e>0，則特征方程(8)有三個正實根；

⑤ 如果e<0，μ0>0且a+d+2e<0，則特征方程(8)有兩個負實根，一個正實根；

⑥ 如果e<0，μ0<0，則特征方程(8)有兩個正實根，一個負實根；

2) 當Δ2<0且μ0≠0時，特征方程(8)有一個實數根和一對復共軛根：

① 如果e>0且a+d+2e>0，則特征方程(8)有一個負實根和一對實部為正的復共軛特征根；

② 如果e>0且a+d+2e<0，則特征方程(8)有一個負實根和一對實部為負的復共軛特征根；

表2 特征方程(8)的根在空間(a,b,c,d,e)中的分布Tab. 2 Distribution of roots of Eq.(8) in (a,b,c,d,e)-space

③ 如果e<0且a+d+2e>0，則特征方程(8)有一個正實根和一對實部為正的復共軛特征根；

④ 如果e<0且a+d+2e<0，則特征方程(8)有一個正實根和一對實部為負的復共軛特征根。

由引理3可以看出曲線Δ2=0,e=0,μ0=0,a+d+2e=0將空間(a,b,c,d,e)分成了如表2所示的10個區域。

由引理3，可得系統(4)在平衡點E(0,0,e)處的穩定性結果。

定理2

1) 如果(a,b,c,d,e)∈S2∪S8，則系統(4)在平衡點E(0,0,e)處對所有的α∈(0,1]都是局部漸近穩定的。

2) 如果(a,b,c,d,e)∈S1∪S3∪S4∪S5∪S6∪S9∪S10，則系統(4)在平衡點E(0,0,e)處對所有的α∈(0,1]都是不穩定的。

3) 如果(a,b,c,d,e)∈S7且α滿足下列不等式

則系統 (4) 在平衡點E(0,0,e)處是局部漸近穩定的。

4) 如果(a,b,c,d,e)∈S7且α滿足下列不等式

則系統 (4) 在平衡點E(0,0,e)處是不穩定的。

證明：同定理1的證明，此處不再贅述。

3 數值仿真

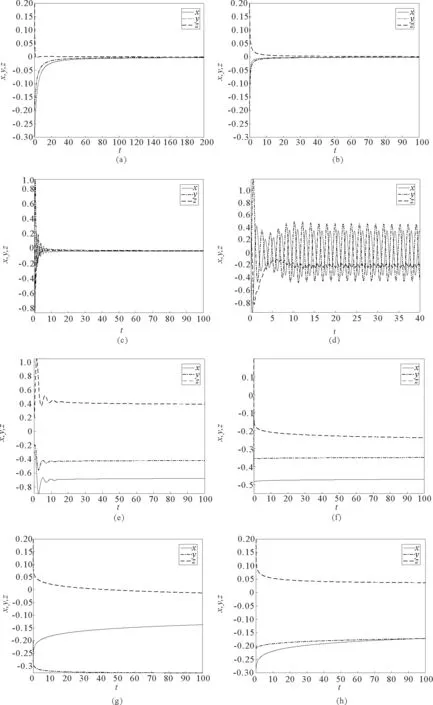
圖1 Langford系統在平衡點處的穩定性Fig.1 Stability of Langford system at equilibrium point

圖1(d)～1(h)表明系統(4)在平衡點O(0,0,0)處是不穩定的，其中圖1(d)與1(c)的系統參數值相同，只改變階數α，圖(d)的階數取值為α=0.8>α*；圖1(e)的系統參數取值為(a,b,c,d,e)=(-1,1,1,-2,2)∈Ω2，階數取值為α=0.6；圖1(f)的系統參數取值為(a,b,c,d,e)=(0.4,0.2,0.3,0.2,-0.1)∈Ω4，階數取值為α=0.03；圖1(g)的系統參數取值為(a,b,c,d,e)=(0.01,-0.3,0.1,0.2,0.1)∈Ω7，階數取值為α=0.1；圖1(h)的系統參數取值為(a,b,c,d,e)=(-0.01,-0.3,0.1,-0.2,0.1)∈Ω8，階數取值為α=0.2。

4 結論

分數階非線性系統的穩定性對實際應用問題有著十分重要的作用，本研究利用Caputo分數階微分定義將三維整數階Langford系統推廣到分數階上，并通過對系統參數的討論判斷了系統的穩定性，最后用Matlab進行數值仿真驗證所得定理的正確性。