基于RBF神經(jīng)網(wǎng)絡(luò)的多移動(dòng)機(jī)械臂同步控制

2

(1. 中國(guó)石油大學(xué)(華東) 化學(xué)工程學(xué)院,山東 青島 266580；2. 合肥通用機(jī)械研究院有限公司，安徽 合肥 230031)

在現(xiàn)代工業(yè)制造過(guò)程中，機(jī)械臂操作系統(tǒng)已經(jīng)迅速被開(kāi)發(fā)并得到了廣泛應(yīng)用，例如組裝、運(yùn)輸、焊接、噴漆以及其他各種高危高難度的復(fù)雜任務(wù)[1-2]。這些任務(wù)需要大量的操作和很好的可操控性，其中大多數(shù)都不能通過(guò)一個(gè)單獨(dú)的機(jī)械臂來(lái)實(shí)現(xiàn)。而固定基座機(jī)械臂系統(tǒng)的工作空間有一定的局限性，因此，多移動(dòng)機(jī)械臂的應(yīng)用得到了廣泛的關(guān)注[3-4]。多移動(dòng)機(jī)械臂系統(tǒng)是一種復(fù)雜的強(qiáng)耦合時(shí)變系統(tǒng)，具有極強(qiáng)的非線性特征。多個(gè)機(jī)械臂之間如何協(xié)同配合，以及怎樣解決兩個(gè)子系統(tǒng)之間的耦合關(guān)系，對(duì)其建立統(tǒng)一數(shù)學(xué)模型并設(shè)計(jì)同步控制器，成為該系統(tǒng)同步控制問(wèn)題的關(guān)鍵[5-6]。對(duì)于多移動(dòng)機(jī)械臂同步控制問(wèn)題的研究，國(guó)內(nèi)外的諸多學(xué)者近幾年已經(jīng)取得了很大的進(jìn)展[7]。

林冠楠[8]針對(duì)移動(dòng)機(jī)械臂的同步控制問(wèn)題，將運(yùn)動(dòng)解耦、機(jī)械臂與移動(dòng)平臺(tái)分開(kāi)進(jìn)行控制，分別針對(duì)兩者設(shè)計(jì)了基于自抗擾技術(shù)的同步控制器。Liu等[9]針對(duì)機(jī)械臂系統(tǒng)的無(wú)源化控制，研究了動(dòng)力學(xué)參數(shù)不同的機(jī)械臂任務(wù)空間同步控制方法。方牧等[10]對(duì)各移動(dòng)機(jī)械臂在關(guān)節(jié)空間做了軌跡規(guī)劃，并設(shè)計(jì)了基于模型參考的自適應(yīng)控制器，但當(dāng)較強(qiáng)的耦合關(guān)系存在于多個(gè)移動(dòng)機(jī)械臂之間時(shí)該控制器并不能獲得很好的控制性能。Desai等[11]對(duì)移動(dòng)平臺(tái)的軌跡進(jìn)行了規(guī)劃，為保證末端機(jī)械手能夠穩(wěn)定操作物體設(shè)計(jì)了相應(yīng)的控制器，但移動(dòng)機(jī)械臂末端機(jī)械手對(duì)被操作物體所施加作用力的魯棒性該控制方法無(wú)法實(shí)現(xiàn)。Sugar等[12]針對(duì)多移動(dòng)機(jī)械臂系統(tǒng)設(shè)計(jì)了基于主從式通信網(wǎng)絡(luò)的同步控制算法，主動(dòng)移動(dòng)機(jī)械臂的路徑方案和力規(guī)劃可以依靠自身來(lái)完成，從動(dòng)移動(dòng)機(jī)械臂與主動(dòng)移動(dòng)機(jī)械臂的運(yùn)動(dòng)狀態(tài)保持一致，對(duì)各自期望軌跡的追蹤可以通過(guò)所設(shè)計(jì)的控制器來(lái)完成。

雖然關(guān)于多移動(dòng)機(jī)械臂的同步控制問(wèn)題到目前為止已經(jīng)取得了很大進(jìn)展，但系統(tǒng)不確定性和主動(dòng)控制力矩的估計(jì)等問(wèn)題并沒(méi)有得到很好的解決，許多先進(jìn)控制算法如RBF(radial basis function,徑向基函數(shù))神經(jīng)網(wǎng)絡(luò)等，未在多移動(dòng)機(jī)械臂系統(tǒng)的同步控制中得到充分的應(yīng)用。因此，本研究在對(duì)多移動(dòng)機(jī)械臂系統(tǒng)動(dòng)力學(xué)特性進(jìn)行分析的基礎(chǔ)上，基于RBF神經(jīng)網(wǎng)絡(luò)，設(shè)計(jì)了一種新的自適應(yīng)主從同步控制器，解決多移動(dòng)機(jī)械臂系統(tǒng)同步控制的相關(guān)問(wèn)題。

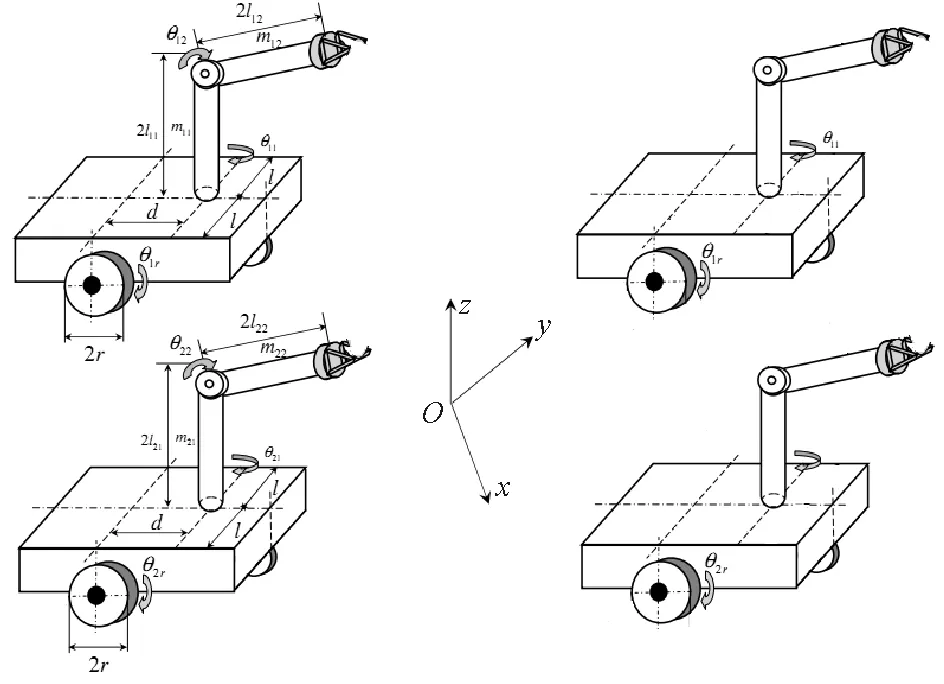
圖1 多移動(dòng)機(jī)械臂主從同步控制系統(tǒng)Fig.1 Synchronous control system of multiple mobile manipulators

1 系統(tǒng)描述

1.1 動(dòng)力學(xué)模型

考慮如圖1所示的多移動(dòng)機(jī)械臂系統(tǒng)，由一個(gè)主動(dòng)機(jī)械臂和n個(gè)從動(dòng)機(jī)械臂所構(gòu)成，且所有機(jī)械臂均具有同樣的結(jié)構(gòu)和動(dòng)力學(xué)參數(shù)，系統(tǒng)模型如圖1所示。

在關(guān)節(jié)空間內(nèi)，其拉格朗日動(dòng)力學(xué)方程可以表示為：

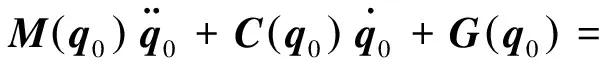
(1)

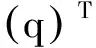
消掉微分約束引入的約束力項(xiàng)，多移動(dòng)機(jī)械臂系統(tǒng)動(dòng)力學(xué)方程可化為：

(2)

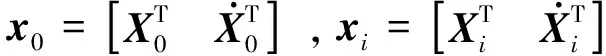
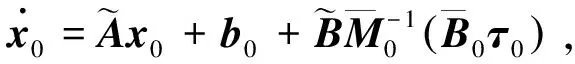
(3)

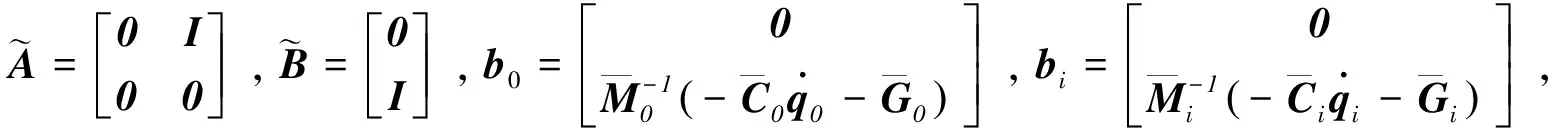
1.2 系統(tǒng)同步誤差

將主、從動(dòng)機(jī)械臂間的同步誤差定義為如下形式：

εi=xi-x0。

(4)

將公式(3)代入并整理可得：

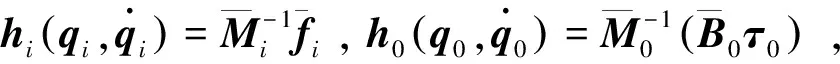
(5)

則本研究的控制任務(wù)為：基于RBF神經(jīng)網(wǎng)絡(luò)，根據(jù)誤差方程式(5)，設(shè)計(jì)一種多移動(dòng)機(jī)械臂系統(tǒng)的同步控制算法，對(duì)系統(tǒng)未知項(xiàng)進(jìn)行估計(jì)和補(bǔ)償，使同步誤差最終收斂至零，從而實(shí)現(xiàn)多移動(dòng)機(jī)械臂系統(tǒng)的主從同步控制。

2 RBF神經(jīng)網(wǎng)絡(luò)主從同步控制器設(shè)計(jì)

根據(jù)已有相關(guān)文獻(xiàn)可知，RBF神經(jīng)網(wǎng)絡(luò)在非線性系統(tǒng)中已獲得一定的應(yīng)用，并且能夠?qū)ο到y(tǒng)非線性進(jìn)行補(bǔ)償[13-14]。所以，本研究將利用RBF神經(jīng)網(wǎng)絡(luò)對(duì)未知狀態(tài)進(jìn)行估計(jì)，并針對(duì)上述機(jī)械臂系統(tǒng)，設(shè)計(jì)一種自適應(yīng)主從同步控制算法，使得該系統(tǒng)在存在系統(tǒng)不確定性和外界干擾的情況下也可以實(shí)現(xiàn)同步運(yùn)動(dòng)，完成上節(jié)所述的同步控制任務(wù)[15]。

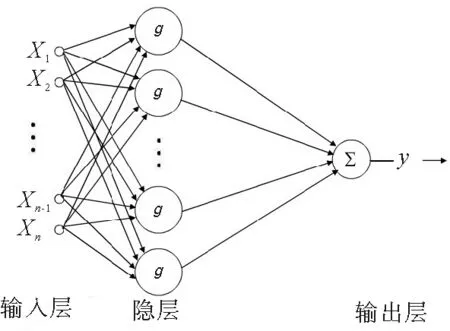
圖2 RBF神經(jīng)網(wǎng)絡(luò)映射關(guān)系Fig.2 Mapping relations ofRBF neural network

2.1 徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)

RBF神經(jīng)網(wǎng)絡(luò)由輸入層、隱層和輸出層構(gòu)成[16]，具有很好的泛化能力，可以使學(xué)習(xí)速率大幅提升，符合實(shí)時(shí)控制的條件，并且能夠防止局部極小值的出現(xiàn)。

輸入向量x與輸出y之間的映射關(guān)系可以用如下公式來(lái)表示：

(6)

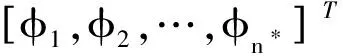
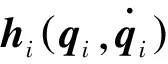
其中，l∈Rmr是一個(gè)緊集，n*的值可以根據(jù)f(x)、ε0合理選擇。

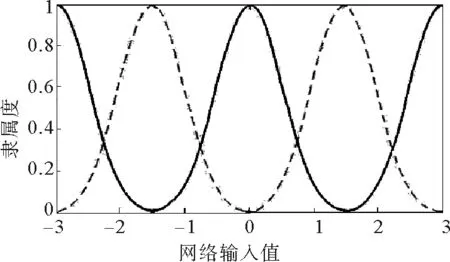
圖3 基于高斯基函數(shù)的隸屬度函數(shù)Fig.3 Membership function based on gauss function

2.2 從動(dòng)移動(dòng)機(jī)械臂動(dòng)力學(xué)補(bǔ)償

矩陣注1：對(duì)于矩陣R，其弗羅貝尼烏斯矩陣范數(shù)定義為如下形式：

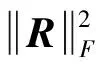
其中，tr(·)表示矩陣的跡。

假設(shè)3：神經(jīng)網(wǎng)絡(luò)中所有權(quán)重系數(shù)矩陣均從屬于一個(gè)大的緊集B(Mθi){θi:θiF≤Mθi}，其中，任意R(Mθi)>0是均為正數(shù)。那么：

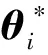
(7)

定義由RBF神經(jīng)網(wǎng)絡(luò)引入的建模誤差ηi為：

ηi

建模誤差ηi的有限正定常數(shù)上界η0i定義為：

η0i

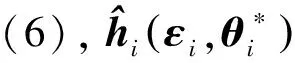
漏電保護(hù)器按其保護(hù)功能和結(jié)構(gòu)特征分類：漏電保護(hù)開(kāi)關(guān).它由零序電流互感器、漏電脫扣器和主開(kāi)關(guān)組裝在一絕緣外殼之中，具有漏電保護(hù)及手動(dòng)通斷電路的功能，但不具有過(guò)負(fù)荷和短路保護(hù)的功能.這類產(chǎn)品主要用于住宅，通稱漏電開(kāi)關(guān).漏電斷路器.它是在低壓斷路器的基礎(chǔ)上加裝漏電保護(hù)部件組成，具有漏電保護(hù)和過(guò)負(fù)荷及短路保護(hù)的功能.它在家用及類似場(chǎng)所廣泛應(yīng)用.漏電繼電器.它由零序電流互感器和繼電器組成，具有檢測(cè)和判斷漏電和接地故障的功能，由繼電器發(fā)出信號(hào)，并控制斷路器或接觸器切斷電路.漏電保護(hù)插座.它由漏電開(kāi)關(guān)或漏電斷路器與插座組合而成，使插座回路連接的設(shè)備具有漏電保護(hù)功能.

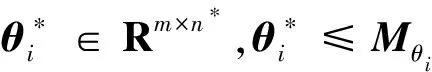
2.3 主動(dòng)移動(dòng)機(jī)械臂控制力矩估計(jì)

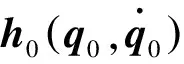
假設(shè)4：神經(jīng)網(wǎng)絡(luò)所有的權(quán)重系數(shù)都屬于一個(gè)大的緊集B(Mθ0){θ0:θ0F≤Mθ0}，其中任意R(Mθ0)>0是均為正數(shù)。那么：

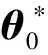
(8)

定義由RBF神經(jīng)網(wǎng)絡(luò)引入的建模誤差η0l為：

η0l

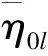
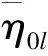
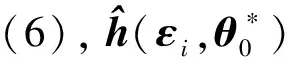
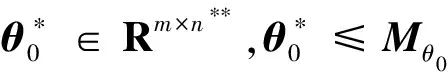
2.4 主從同步控制器設(shè)計(jì)

在前面兩節(jié)的基礎(chǔ)上，基于RBF神經(jīng)網(wǎng)絡(luò)的多移動(dòng)機(jī)械臂分布式自適應(yīng)同步控制器可以設(shè)計(jì)為如下形式：

τi=τ1+τ2+τ3，

(9)

(10)

(11)

(12)

(13)

(14)

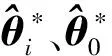
(15)

在控制器設(shè)計(jì)中，τi1用來(lái)抵消哥氏力和重力；τi2可以消除主從機(jī)械臂間的同步誤差；τi3可以抵消主動(dòng)機(jī)械臂輸入力矩的擾動(dòng)。

2.5 Lyapunov穩(wěn)定性分析

將2.4節(jié)設(shè)計(jì)的控制器代入式(5)，可得：

(16)

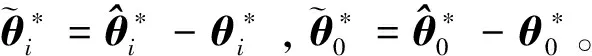
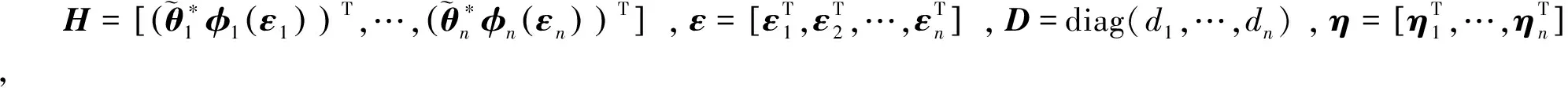
(17)

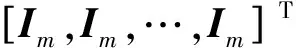
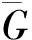
定理1在滿足假設(shè)1～5的條件下，針對(duì)公式(1)、(2)所示的多移動(dòng)機(jī)械臂系統(tǒng)，在主從同步控制律(9)～(15)的作用下，通過(guò)適當(dāng)?shù)剡x取矩陣Q≥0，可以在任意初始狀態(tài)下，使從動(dòng)移動(dòng)機(jī)械臂對(duì)主動(dòng)機(jī)械臂移動(dòng)軌跡實(shí)現(xiàn)跟蹤，且同步誤差εi可以收斂至一個(gè)小的剩余集。

證明：選擇式(18)所示的Lyapunov函數(shù)

(18)

將公式(18)兩邊同時(shí)對(duì)時(shí)間求導(dǎo)可得：

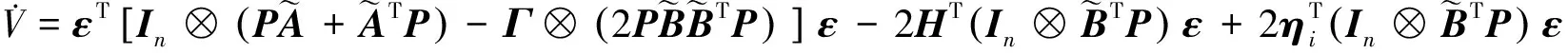
利用文獻(xiàn)[18]中的方法對(duì)方程進(jìn)行放縮，可得：

將控制器中自適應(yīng)律(13)、(14)帶入并整理可得：

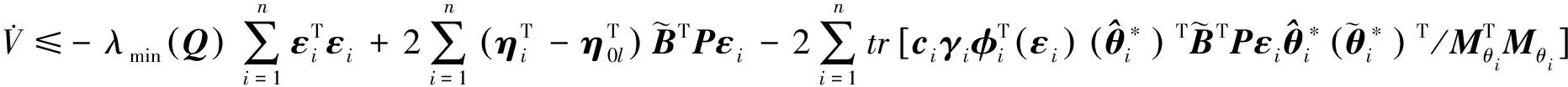
上述李雅普諾夫函數(shù)的微分不等式可整理為：

(19)

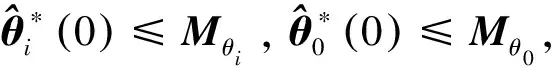
3 Matlab仿真驗(yàn)證

選取由5個(gè)二連桿機(jī)械臂構(gòu)成的多移動(dòng)機(jī)械臂系統(tǒng)，進(jìn)行Matlab仿真，驗(yàn)證本研究所提出的主從同步控制律(9)～(15)的穩(wěn)定性和有效性。其中下標(biāo)1表示主動(dòng)機(jī)械臂，其余為從動(dòng)機(jī)械臂。

3.1 基本參數(shù)設(shè)定

機(jī)械臂動(dòng)力學(xué)方程如下：

其中，模型不確定性為如下形式：

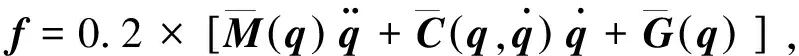
相關(guān)參數(shù)設(shè)置為：

m0=50 kg，m1=4 kg，m2=3.5 kg，R=0.3 m，d=0.3 m，J0=1.417 kg·m2，

J1=0.03 kg·m2，J2=0.036 kg·m2，r=0.1 m，L1=0.5 m，L2=0.35 m。

主動(dòng)移動(dòng)機(jī)械臂期望軌跡如下：

xcd=0.2t,ycd=0.2t,

xEd=0.2t,yEd=0.1sin(2t)+0.2t+0.15。

各移動(dòng)機(jī)械臂的初始狀態(tài)分別設(shè)置為：

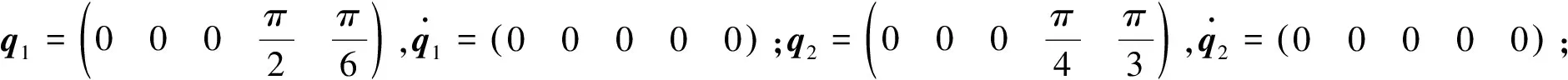
反饋增益K及自適應(yīng)律相關(guān)參數(shù)γ0、γi等分別設(shè)置為：

拉普拉斯矩陣L、D以及所選擇的正定矩陣Q、常數(shù)δ分別設(shè)置為：

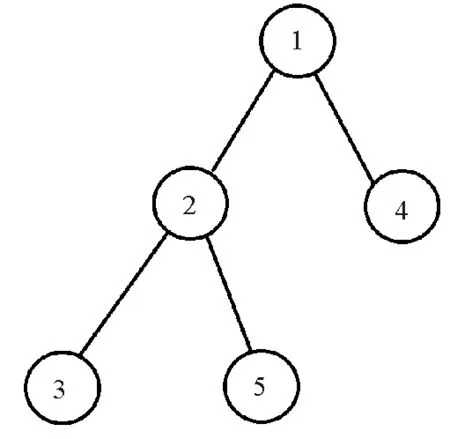
圖4 通訊拓?fù)浣Y(jié)構(gòu)Fig.4 Communication topology structure

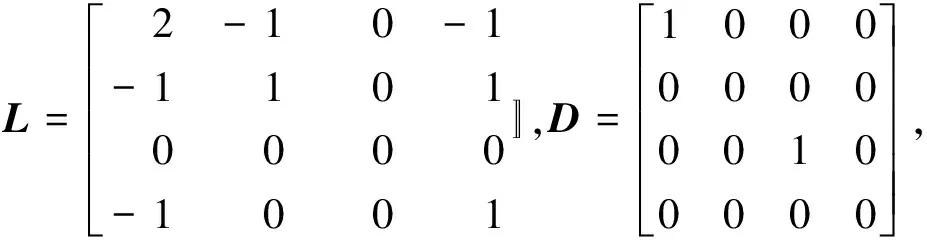
Q=10.267 9×diag(1,1,1,1,1,1,1,1),

δ=0.367 9。

選取如圖4中的通訊拓?fù)浣Y(jié)構(gòu)。其中，信息可以由主動(dòng)移動(dòng)機(jī)械臂1傳遞給從動(dòng)移動(dòng)機(jī)械臂2和4，但無(wú)法反向進(jìn)行傳遞。

3.2 Matlab仿真結(jié)果及分析

在上述研究基礎(chǔ)上對(duì)此多移動(dòng)機(jī)械臂系統(tǒng)進(jìn)行Matlab仿真，仿真結(jié)果見(jiàn)圖5～14。

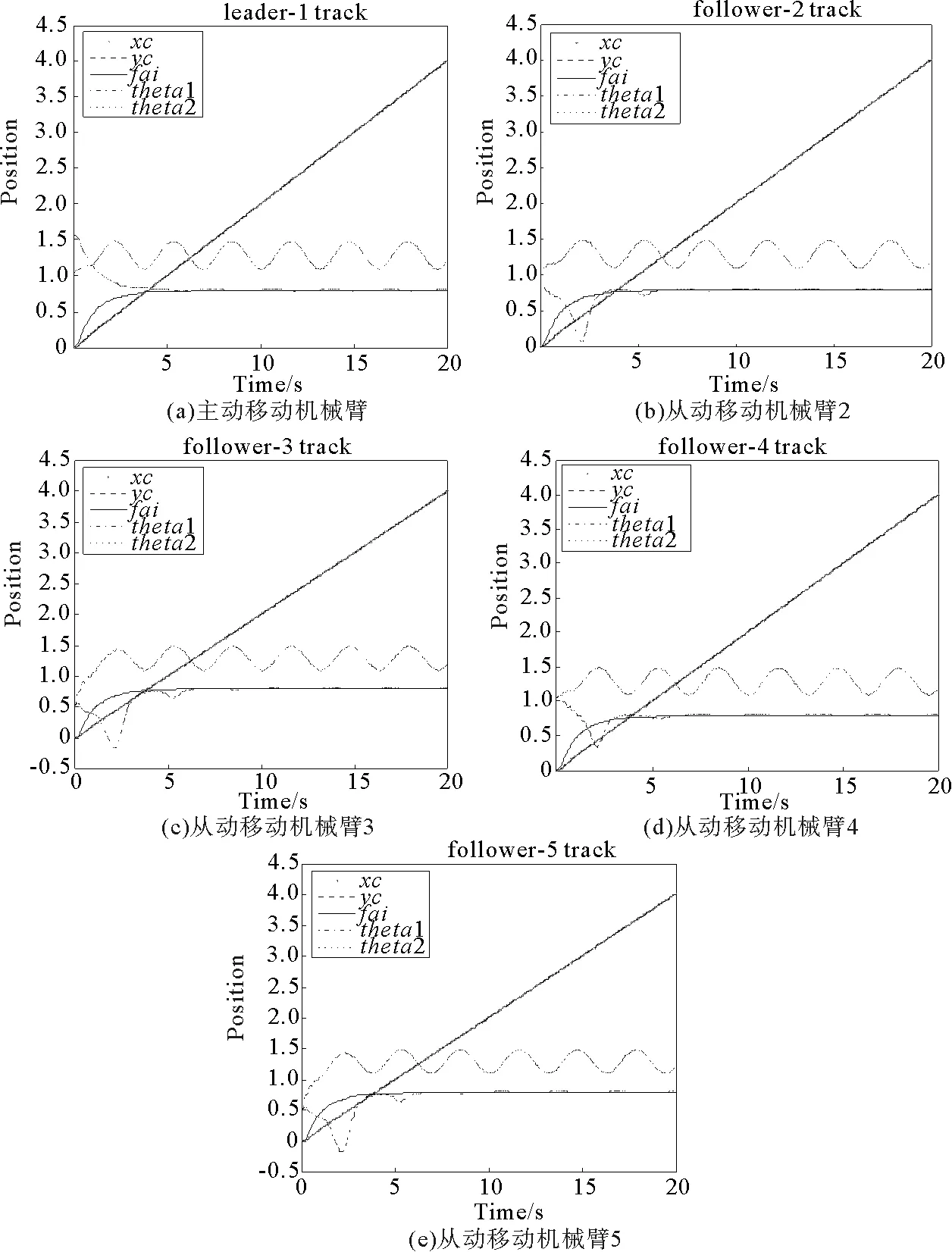
圖5 主動(dòng)移動(dòng)機(jī)械臂及從動(dòng)移動(dòng)機(jī)械臂2～5運(yùn)動(dòng)軌跡Fig.5 Movement trajectories of leader mobile robot and follower mobile robots 2-5

通過(guò)仿真結(jié)果圖5可以看出，多移動(dòng)機(jī)械臂系統(tǒng)在主從同步控制器(9)～(15)的控制作用下，主動(dòng)機(jī)械臂可以對(duì)預(yù)定軌跡實(shí)現(xiàn)快速跟蹤；從動(dòng)機(jī)械臂在初始狀態(tài)各不相同的情況下，也可以快速對(duì)主動(dòng)機(jī)械臂移動(dòng)軌跡進(jìn)行跟蹤，并且整個(gè)系統(tǒng)在達(dá)到穩(wěn)定狀態(tài)后未再產(chǎn)生較大波動(dòng)。

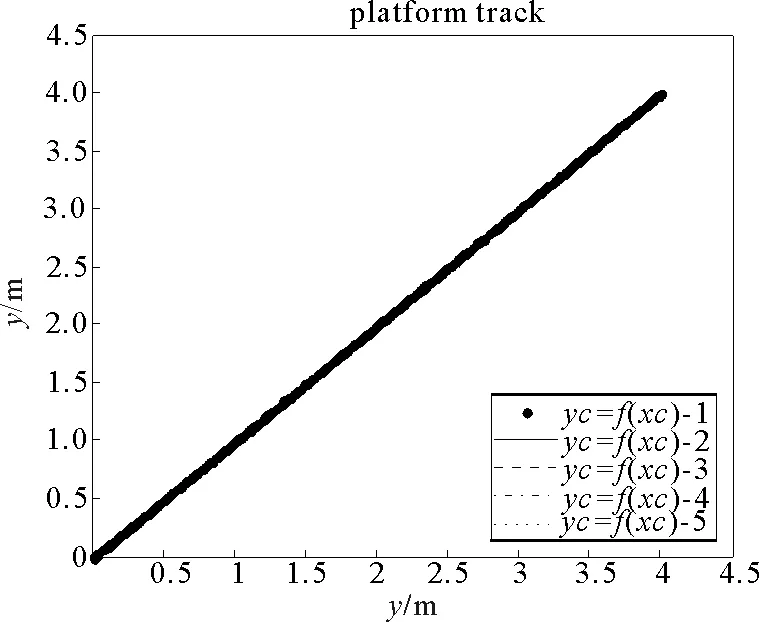
圖6 各移動(dòng)平臺(tái)質(zhì)心位置Fig.6 Mass center position of each mobile platform

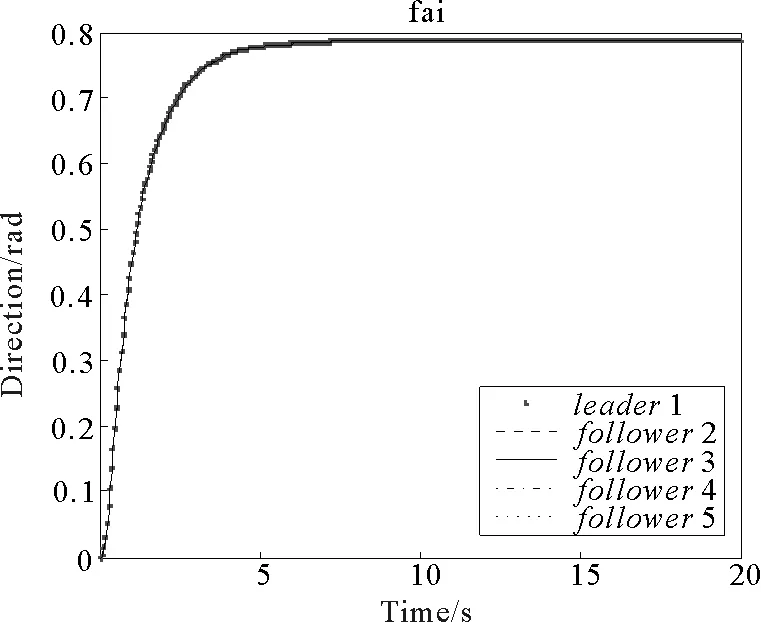
圖7 各移動(dòng)平臺(tái)方向角Fig.7 Direction angle of each mobile platform

由仿真結(jié)果圖6～7可以看出，在同步控制器(9)～(15)的控制下，各平臺(tái)移動(dòng)軌跡及前進(jìn)方向角均保持相同，即能夠準(zhǔn)確使平臺(tái)間誤差收斂到零，從而為多移動(dòng)機(jī)械臂系統(tǒng)實(shí)現(xiàn)同步運(yùn)動(dòng)提供了保證。

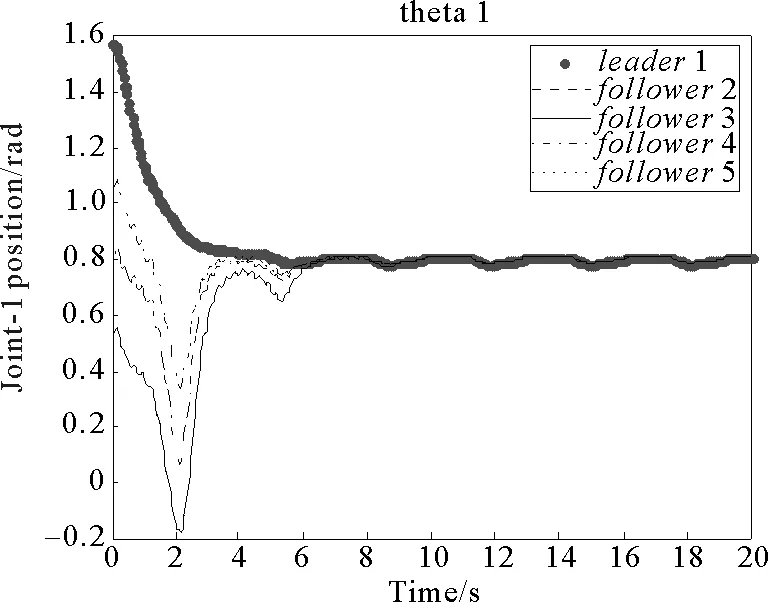
圖8 關(guān)節(jié)1位置變化曲線Fig.8 Position change curve of joint 1

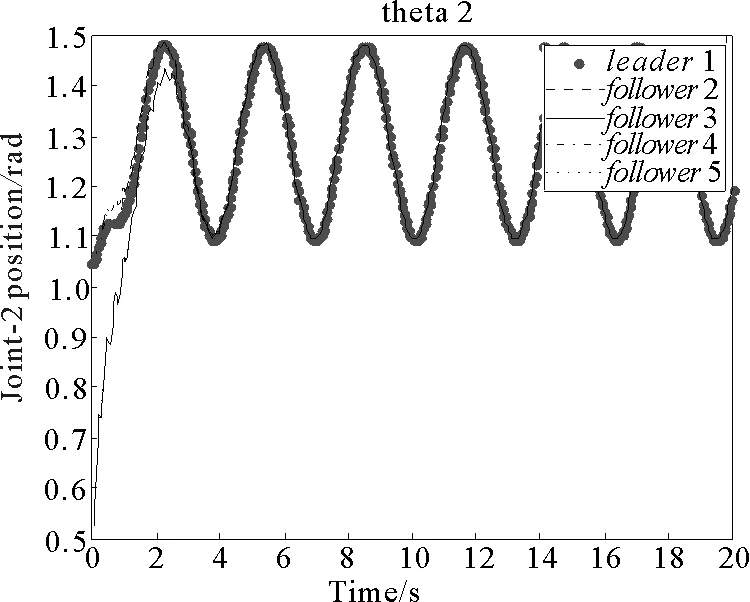
圖9 關(guān)節(jié)2位置變化曲線Fig.9 Position change curve of joint 2

通過(guò)仿真結(jié)果圖8和圖9可以看出，在7 s左右時(shí)，主動(dòng)移動(dòng)機(jī)械臂和從動(dòng)移動(dòng)機(jī)械臂中關(guān)節(jié)1的位置誤差基本漸近收斂到零；在4 s左右時(shí)，主、從移動(dòng)機(jī)械臂關(guān)節(jié)2的位置誤差基本漸近收斂到零，且穩(wěn)定后均不再發(fā)生較大波動(dòng)。在4～7 s之間時(shí)，關(guān)節(jié)1和關(guān)節(jié)2同步誤差共同漸近收斂到零。由仿真結(jié)果圖10可以看出，在4 s左右時(shí)，各移動(dòng)平臺(tái)方向的角速度誤差能夠收斂到零。由圖11和圖12可知，分別在10 s和8 s左右時(shí)，各移動(dòng)機(jī)械臂關(guān)節(jié)1和關(guān)節(jié)2處的速度誤差均能分別漸近收斂到零。

綜合分析仿真結(jié)果圖11～12可知：通過(guò)適當(dāng)?shù)剡x擇控制器參數(shù)，在本研究所設(shè)計(jì)的主從同步控制算法(9)～(15)的控制作用下，在初始階段即使存在一定偏差，同理論分析一樣，從動(dòng)移動(dòng)機(jī)械臂的平臺(tái)方向角速度及二連桿機(jī)械臂兩個(gè)關(guān)節(jié)的運(yùn)動(dòng)速度均能迅速、高精度地同步于主動(dòng)機(jī)械臂，即主、從機(jī)械臂之間的速度誤差能夠收斂到零，且在達(dá)到穩(wěn)定狀態(tài)之后不再發(fā)生較大波動(dòng)。

通過(guò)仿真結(jié)果圖13～14可知，各移動(dòng)機(jī)械臂的輸入力矩均有界。

綜合分析仿真結(jié)果5～14，可以得到如下結(jié)論：在考慮各移動(dòng)機(jī)械臂中移動(dòng)平臺(tái)和二連桿機(jī)械臂之間交互影響條件下，通過(guò)合理設(shè)計(jì)控制器參數(shù)，利用所提出的基于RBF神經(jīng)網(wǎng)絡(luò)的主從同步控制算法(9)～(15)，可以抵消主動(dòng)移動(dòng)機(jī)械臂輸入控制力矩的影響，估計(jì)從動(dòng)移動(dòng)機(jī)械臂的建模誤差并進(jìn)行補(bǔ)償，使各移動(dòng)機(jī)械臂之間同步誤差漸近收斂到零，保證多移動(dòng)機(jī)械臂實(shí)現(xiàn)同步運(yùn)動(dòng)。

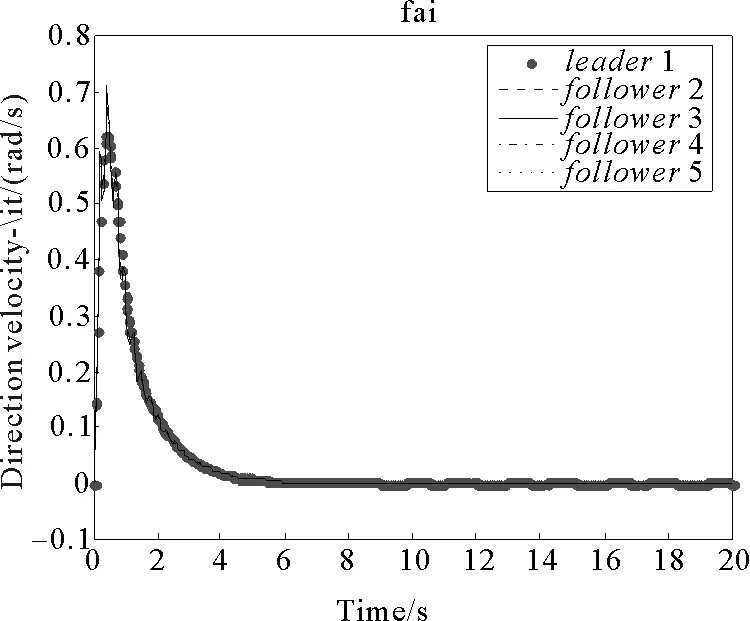
圖10 各移動(dòng)平臺(tái)方向角速度變化曲線Fig.10 Angular velocity curve of each mobile platform

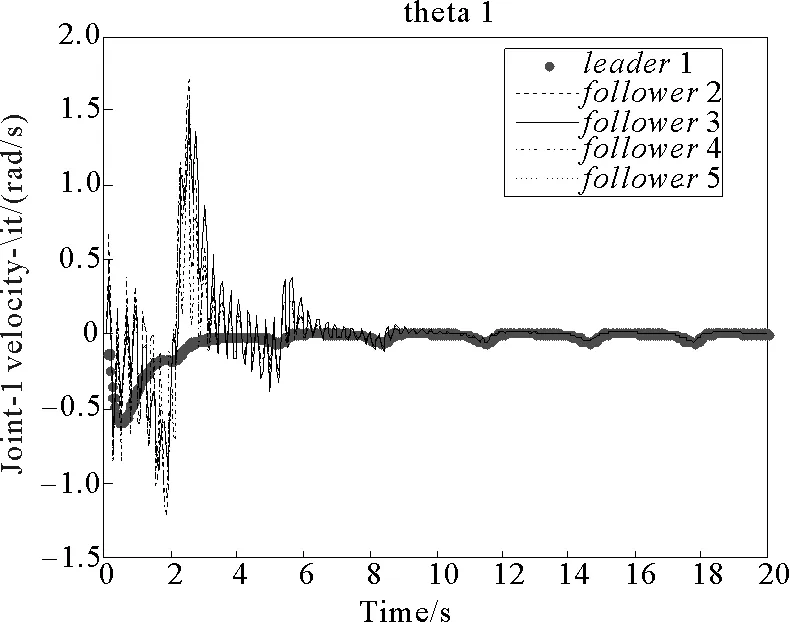
圖11 關(guān)節(jié)1速度變化曲線Fig.11 Velocity change curve of joint 1

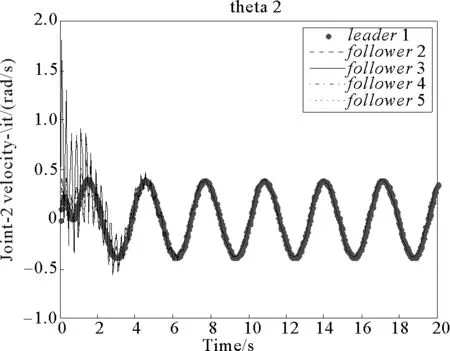
圖12 關(guān)節(jié)2速度變化曲線 Fig.12 Velocity change curve of joint 2

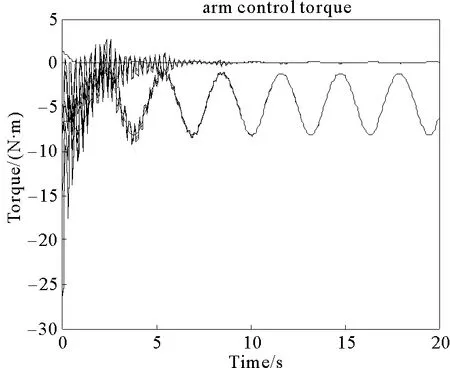
圖13 主從機(jī)械臂二連桿關(guān)節(jié)驅(qū)動(dòng)力矩Fig.13 Joint driving torque of the two connectingrod of the leader and follower manipulators

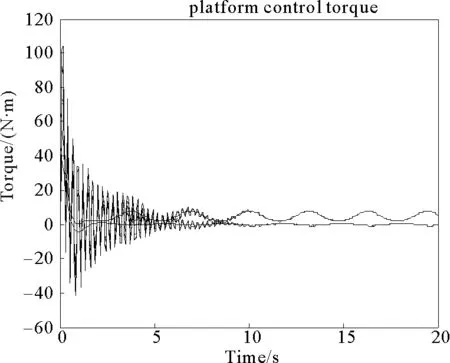
圖14 主從移動(dòng)機(jī)械臂移動(dòng)平臺(tái)左右輪驅(qū)動(dòng)力矩Fig.14 Left and right wheel driving torques of the platforms of the leader and follower manipulators

4 結(jié)論

利用RBF神經(jīng)網(wǎng)絡(luò)和領(lǐng)導(dǎo)者-追隨者通信拓?fù)涞姆椒ǎ槍?duì)多移動(dòng)機(jī)械臂同步控制系統(tǒng)，設(shè)計(jì)了一種新的分布式自適應(yīng)主從同步控制算法。主要結(jié)論有：

1) 主動(dòng)移動(dòng)機(jī)械臂和從動(dòng)移動(dòng)機(jī)械臂之間的同步誤差通過(guò)領(lǐng)導(dǎo)者-追隨者通信拓?fù)渚W(wǎng)絡(luò)結(jié)構(gòu)來(lái)進(jìn)行了定義；

2) 利用RBF神經(jīng)網(wǎng)絡(luò)，對(duì)從動(dòng)移動(dòng)機(jī)械臂的模型誤差等系統(tǒng)不確定性進(jìn)行了逼近和補(bǔ)償，并對(duì)主動(dòng)移動(dòng)機(jī)械臂的控制力矩進(jìn)行了估計(jì)；

3) 所設(shè)計(jì)的同步控制器可以使同步誤差漸進(jìn)收斂到零，在存在較大初始誤差的情況下也能夠?qū)崿F(xiàn)多移動(dòng)機(jī)械臂的同步控制。