不同階次的分數階復值混沌系統的廣義投影同步和廣義錯位投影同步
(山東科技大學 數學與系統科學學院,山東 青島 266590)
分數階微積分具有和整數階微分理論近乎同樣長的歷史,但由于人們的認知水平不足、缺乏對應的物理應用背景等原因,分數階微分一直沒得到相應的發展和重視[1]。直到1982年,Mandelbrot等[2]第一次指出自然界和許多其他領域中存在很多相似于整數階系統的分數維現象;在生物醫學、力學物理、金融工程和神經網絡工程等一些新興領域,用整數微分方程建模存在很大的局限性,但利用分數階微積分可以有效改善遺傳記憶問題[3-5]。此外,由于混沌信號具有初值敏感性、類隨機性、連續寬帶譜等特性,分數階混沌系統在保密通信中具有巨大的潛在價值,可實現數字混沌加密通信,有利于提高信息的安全傳輸[6-7],因此研究分數階系統具有十分重要的意義。
早在1990年,Peora和Corrol[8]就提出了混沌同步的概念,并廣泛應用于物理學、氣象學等各種工程和物理領域中。近年來,混沌同步在保密通信等跨學科領域的潛在應用價值吸引了許多學者的注意[9],并取得了一些重大成果。例如:自適應、脈沖和滑模變結構等同步方法[10-11],完全同步、反同步、投影同步、函數投影同步等[12-14]。相對于整數階系統,分數階系統可以更加準確地描述系統的動態變化,并且控制自由度更高[15],吸引了很多學者對分數階混沌動力學系統同步進行研究,并取得了一系列進展[16-17]。然而,在工程實踐中復值變量更為常見,復值系統在電磁場等領域中具有更重要的應用前景,研究者開展復值系統動力行為的研究,包括分岔、同步和穩定性分析等[17-18]。但目前對于復值分數階系統和階次不等的分數階系統的同步研究還很少[19]。本研究利用混沌同步能增強保密通信的抗破解能力的特點,結合不同階次分數階廣義投影同步和采用復雜多變的比例因子,提出不同階次復值分數階廣義錯位投影同步,提高保密通信的安全傳輸。
1 知識準備與問題描述
1.1 分數階微積分定義
在不同領域的研究中,分數階微積分是對整數階微積分的推廣,在研究過程的實際應用中,定義主要有Grunwald-Letnikov定義、Riemann-Liouville定義和Caputo定義。
Caputo定義數學表達式如下:
(1)
其中n-1<α 因為分數階Caputo微分定義對初始值有敏感性,所以更多的應用在工程領域,與分數階微分對應的是積分: (2) 驅動系統和響應系統數學模型: (3) (4) 其中x=(x1,x2,…xn)T∈Rn,y=(y1,y2,…yn)T∈Rn分別表示驅動系統和響應系統的時間狀態變量;f,g:Rn→Rn,F,G:Rn×n→Rn×n表示非線性函數;A,B表示參數向量,u(t)為要設計的非線性控制器。 定義驅動系統和響應系統同步的誤差向量:e(t)=y(t)-Δx(t), 其中Δ=δij是比例因子矩陣,Δ∈Rn×n為非奇異矩陣,該矩陣每行每列只有一個非零元素值,若Δ為對角矩陣,該同步稱為廣義投影同步,若Δ不是對角矩陣,則此同步為廣義錯位投影同步,要求驅動系統與響應系統的狀態變量不是完全一一對應的,而是按照錯位關系成比例的同步。 (5) 分數階復值Chen混沌系統的數學模型如下: (6) 為研究該系統的非線性動力學行為,取系統參數和階數:a1=35,a2=3,a3=28,α=0.93,α=0.98, 分數階Chen系統處于混沌狀態,混沌吸引子見圖1和圖2。 圖1 相空間中的混沌吸引子(α=0.93)Fig.1 Chaotic attractor in phase space (α=0.93) 圖2 相空間中的混沌吸引子(α=0.98)Fig.2 Chaotic attractor in phase space (α=0.98) 研究驅動系統和響應系統階次不等情況下的同步,以系統(6)作為驅動系統,以系統(7)作為響應系統,假設響應系統的階次β大于驅動系統的階次α(0<α<β<1),有 (7) 根據分數階微分的定義和引理1知,驅動系統方程(6)可以轉化為: (8) 即 (9) 因此不等階次的分數階復值混沌Chen系統(6)和(7)的同步問題就轉化為混沌系統(9)和(7)的同步問題。 定義系統的同步誤差: (10) 由式(7)、(9)、(10),得到其同步誤差方程: (11) 定理1基于分數階穩定性理論和自適應控制方法,設計控制器如下: (12) 證明:把所設計的控制器(12)代入誤差系統(11)得到新的同步誤差系統: (13) 構造函數h1(e): (14) 根據引理2,在控制器(12)的控制下,分數階誤差系統(11)穩定,定理1得證。 以不同階次分數階復值Chen系統為例,以(6)為驅動系統,以(7)為響應系統,研究廣義錯位投影同步,也就是研究系統(9)和(7)的同步問題,因為驅動系統和響應系統階次都是5,所以廣義錯位投影同步有5!-1=119種,設ni表示第i種錯位形式,i=1,2,3,…,119,xj和yj(j=1,2,3,4,5)表示兩個分數階系統的狀態變量,則有如下119種組合: n1:(x1,y1),(x2,y2),(x3,y3),(x4,y5),(x5,y4); n2:(x1,y1),(x2,y2),(x3,y4),(x4,y5),(x5,y3); n3:(x1,y1),(x2,y2),(x3,y4),(x4,y3),(x5,y5); n4:(x1,y1),(x2,y2),(x3,y5),(x4,y3),(x5,y4); n5:(x1,y1),(x2,y2),(x3,y5),(x4,y4),(x5,y3); ? n119:(x1,y5),(x2,y1),(x3,y2),(x4,y3),(x5,y4)。 這里討論第119種組合n119, 假設存在非奇異矩陣Δ,δij(i,j=1,2,3,4,5)是常數: 其余形式也可用此法進行類似分析,該形式的廣義錯位投影同步誤差為: (15) 由 (7),(9),(15)式,可得同步誤差系統方程: (16) 定理2對于任意給定的非奇異比例因子矩陣Δ和初始值,在自適應控制器(17)的作用下,可實現驅動系統(9)和響應系統(7)的廣義錯位投影同步,設計的非線性控制器如下: (17) 證明:將非線性控制器 (17) 代入誤差系統方程 (16) 得: (18) 構造函數h2(e): +δ45x5(t)e2(t)e5(t)+δ23x3(t)e4(t)e5(t) (19) 由于(19)式滿足引理2,誤差系統(16)穩定于零點,實現了廣義錯位投影同步,定理2得證。 為驗證上述方法的有效性,本節采用求解分數階微分方程計算精度很高的預估校正算法進行數值仿真實驗。 對于第3部分的數值仿真,初始值取x1=1,x2=1,x3=2,x4=2,x5=3,y1=0,y2=0,y3=-2,y4=0,y5=9, 驅動系統階次α=0.96, 響應系統階次β=0.98, 其仿真結果如圖3所示。初始值取x1=1,x2=1,x3=2,x4=2,x5=3,y1=0,y2=-1.5,y3=-2,y4=0,y5=7, 驅動系統階次α=0.93, 響應系統階次β=0.98, 其仿真結果如圖4所示,圖示結果表明在所設計控制器的作用下誤差趨于零,可以實現不同階次復值分數階混沌系統的同步,驗證了所設計控制器的有效性。 圖3 階次0.96的驅動系統和階次0.98的響應系統的廣義投影同步誤差Fig.3 Generalized projective synchronization error of order 0.96 drive system and 0.98 response system 圖4 階次0.93的驅動系統和階次0.98的響應系統的廣義投影同步誤差Fig.4 Generalized projective synchronization error of order 0.93 drive system and 0.98 response system 對于第4部分的數值實驗,比例因子選取δ12=3,δ23=2.5,δ34=2,δ45=1.5,δ51=3,驅動響應系統的階次α=0.96,β=0.98, 初始值選取x1=1,x2=1,x3=2,x4=2,x5=3,y1=0,y2=0,y3=-2,y4=0,y5=9, 同步誤差系統圖見圖5。驅動響應系統的階次選取α=0.93,β=0.98, 初始值選取x1=1,x2=1,x3=2,x4=2,x5=3,y1=0,y2=-1.5,y3=-1,y4=0,y5=7, 同步誤差系統圖見圖6,從圖5和圖6可以看出廣義錯位投影同步誤差系統趨于零,驅動系統和響應系統實現了廣義錯位投影同步,驗證了設計的控制器的有效性。 圖5 階次0.96的驅動系統和階次0.98的響應系統的廣義錯位投影同步誤差Fig.5 Generalized dislocation projective synchronization error of order 0.96 response system and 0.98 response system 圖6 階次0.93的驅動系統和階次0.98的響應系統的廣義錯位投影同步誤差Fig.6 Generalized dislocation projective synchronization error of order 0.93 response system and 0.98 response system 依據分數階微積分的定義和定理,提出一種不同階次復值分數階同步的方法。針對不同分數階階次的復值混沌系統,可以通過將不同分數階階次的復值分數階系統轉化為等階次的復值分數階不同結構的系統進行分析,通過設計非線性控制器實現了廣義投影同步和廣義錯位投影同步,并給出了證明。利用預估校正算法進行數值實驗,得到的仿真結果與數學理論分析一致,該方法的同步效果與以往的混沌同步效果相同,驗證了該方法的正確性。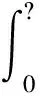

1.2 廣義投影同步和廣義錯位投影同步描述


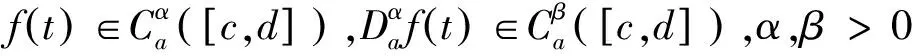
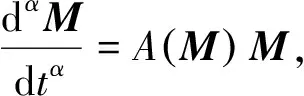
2 分數階復值Chen混沌系統及其不同階次廣義投影同步
2.1 分數階復值Chen混沌系統


2.2 不同階次分數階復值Chen系統廣義投影同步
3 不同階次分數階復值Chen系統廣義錯位投影同步




4 數值仿真




5 結論

