不連續時滯分數階憶阻神經網絡的非線性動力學分析
(山東科技大學 電氣與自動化工程學院, 山東 青島 266590)
1971年,華裔科學家蔡少棠[1]根據概念的對稱性首次提出了憶阻器的概念,描述了磁通和電荷之間的非線性關系。2008年,惠普公司研究團隊首次實現了具有TiO2雙層薄膜結構的實物憶阻器[2]。由于憶阻器的阻值依賴于電壓或電流的作用時間而非當前時刻的瞬時值,從而使得憶阻器成為天然的非易失性存儲器,即當憶阻器兩端電壓(或電流)掉電時,憶阻器仍然能記憶其當前時刻的電阻值。文獻[3]研究表明憶阻器能夠模擬大腦中的神經突觸,由于憶阻器的這種記憶特性,越來越多的研究者用憶阻器代替傳統神經網絡中的電阻來構建憶阻神經網絡[4]。近年來,憶阻神經網絡(memristive neural networks,MNNS)的動力學行為得到了廣泛的研究[5]。
分數階微積分目前在各個領域都得到了廣泛的應用。相較于整數階微積分,分數階微積分最主要的優點在于其具有記憶特性,這使得它為描述具有遺傳和記憶特性的各種物質和過程提供了更新穎的、準確的數學工具[6]。文獻[7]表明分數階微積分能夠更精確地刻畫小鼠大腦新皮層錐體神經元的動力學行為。鑒于此,為了更好地描述大腦神經元的動力學過程,一些研究人員將分數階微積分引入到神經網絡中,建立了分數階神經網絡模型[8]。神經網絡可以由超大規模集成電路(vary large scale integration,VLSI)來實現[9]。在整數階神經網絡中,電容是整數階的。然而,大量研究表明電容實際上是分數階的[10]。為此,研究人員用分數階電容代替整數階電容來構建神經網絡電路,以提高模型的精確度,從而建立了分數階神經網絡。與整數階神經網絡相比,分數階神經網絡的非線性更強,且具有更多自由參數。近年來,關于分數階神經網絡的動力學研究取得了巨大的進展[11]。
為了更精確地描述大腦神經元的動力學行為,研究人員結合憶阻器和分數階微積分的優點建立了分數階憶阻神經網絡模型(fractional memristive neural networks,FMNNS)[12]。從電路實現的角度來看,FMNNs可以通過將整數階憶阻神經網絡中的整數階電容用分數階電容代替來實現。雖然目前關于整數階憶阻神經網絡的動力學研究成果豐碩,但是傳統的分析方法如Lyapunov方法和矩陣測度方法等都不能直接應用到分數階憶阻神經網絡中去。因此,如何將分數階微積分理論的最新研究成果應用到分數階憶阻神經網絡的分析中來是目前急需解決的問題。分數階和憶阻器的引入給神經網絡的動力學分析帶來了巨大的困難和挑戰。近年來,關于分數階憶阻神經網絡的研究已經取得了一些成果[12-17]。文獻[12]利用分數階李雅普諾夫函數方法研究了FMNNs的Mittag-Leffler的穩定性。文獻[14]利用不等式技術研究了時滯FMNNs的自適應同步問題。文獻[15]研究了時滯FMNNs的混合投影同步。文獻[16]利用比較原理研究了參數不確定多時滯FMNNs的同步問題。文獻[17]利用新的Mittag-Leffler估計引理研究了參數不匹配FMNNs的準同步問題。
根據上述討論可知,文獻[5,11]研究的都是連續型神經網絡的動力學,文獻[13]研究了具有不連續憶導函數的FMNN的動力學行為,文獻[12,14-17]主要研究了不連續憶阻神經網絡的穩定性和同步問題。目前尚沒有文獻對不連續時滯FMNN的非線性動力學進行研究。為此,提出了一個不連續時滯分數階憶阻神經網絡模型,并研究了不同的分岔參數對系統動力學行為的影響。值得注意的是,不連續時滯分數階憶阻神經網絡的連接權重不同,使得其包含多個子系統。系統隨開關階躍T的變化而切換,使系統的動力學行為更加復雜。另外,文獻[5,11]中提出的系統通往混沌的道路大多為倍周期分岔或反向倍周期分岔,而本研究提出的FMNN模型通往混沌的道路為陣發混沌,動力學行為更加豐富。不連續憶導函數和開關階躍的加入能夠極大地豐富系統的動力學行為,所得結果為不連續FMNN的應用打下基礎。
1 預備知識
1.1 Caputo 型分數階導數
定義 1[18] 函數f(t)的α階Caputo型分數階導數定義如下:
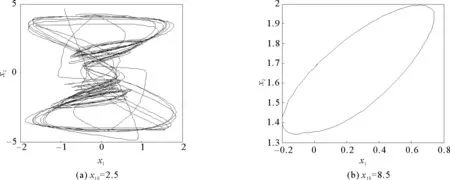
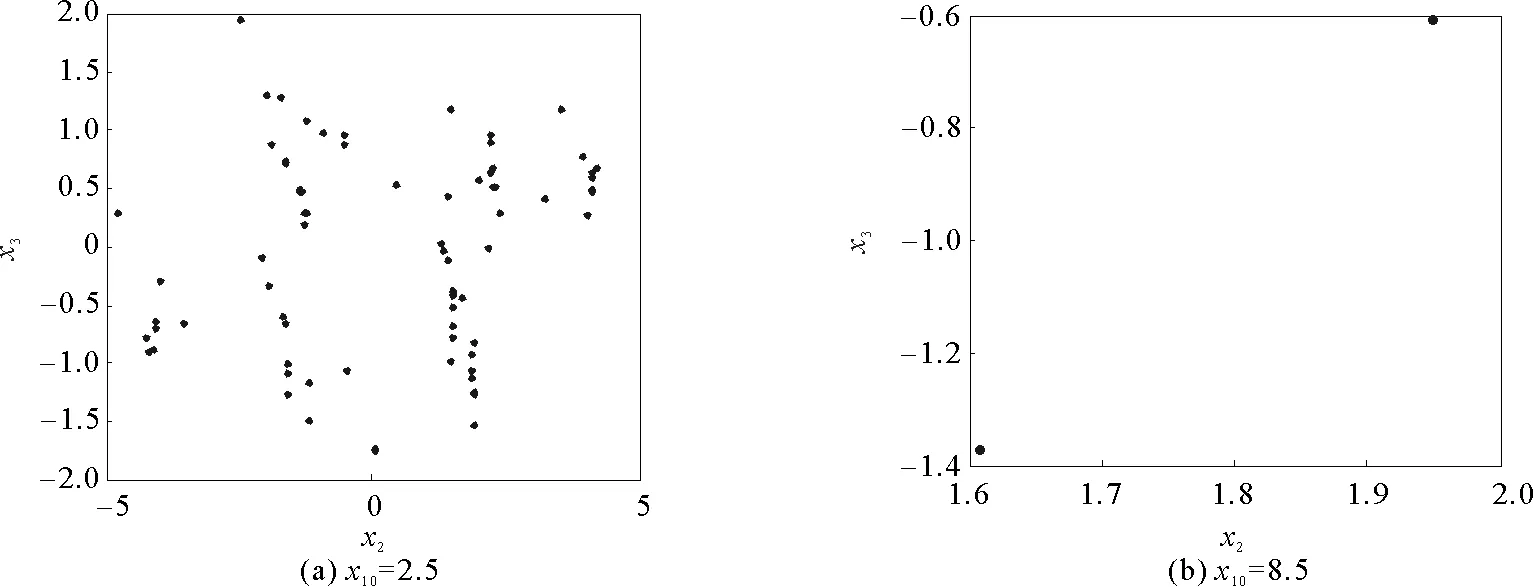
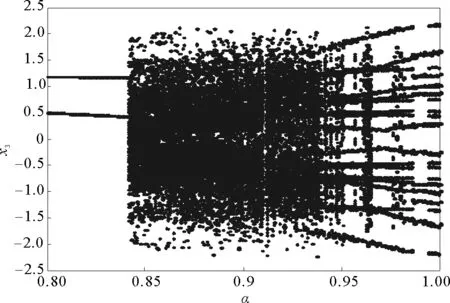
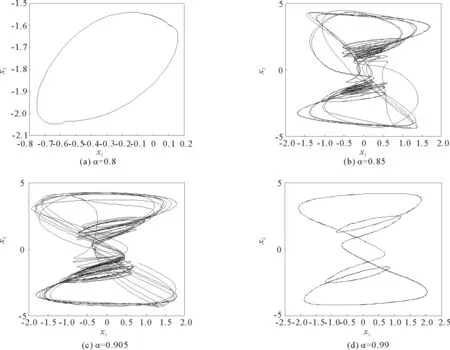
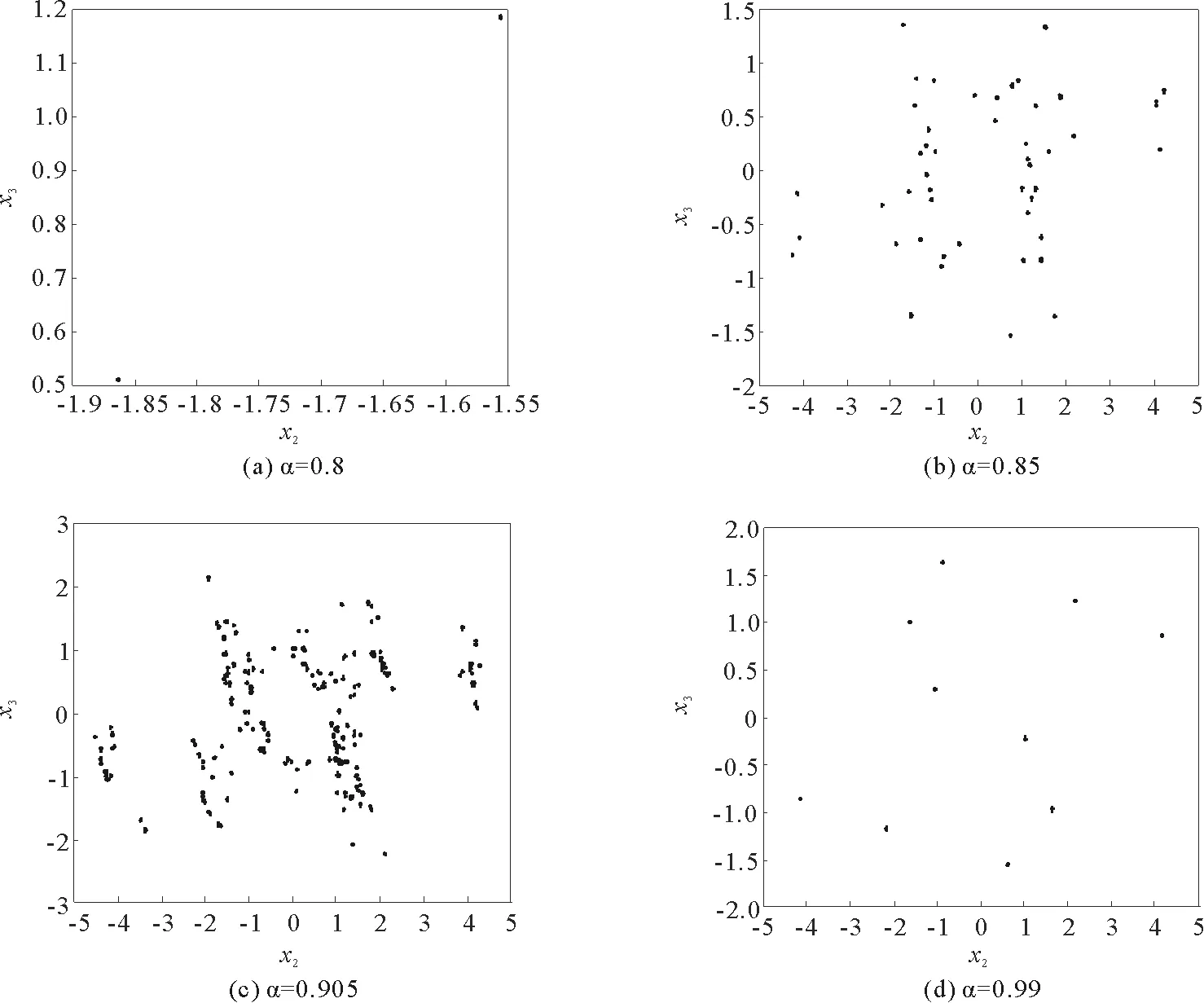
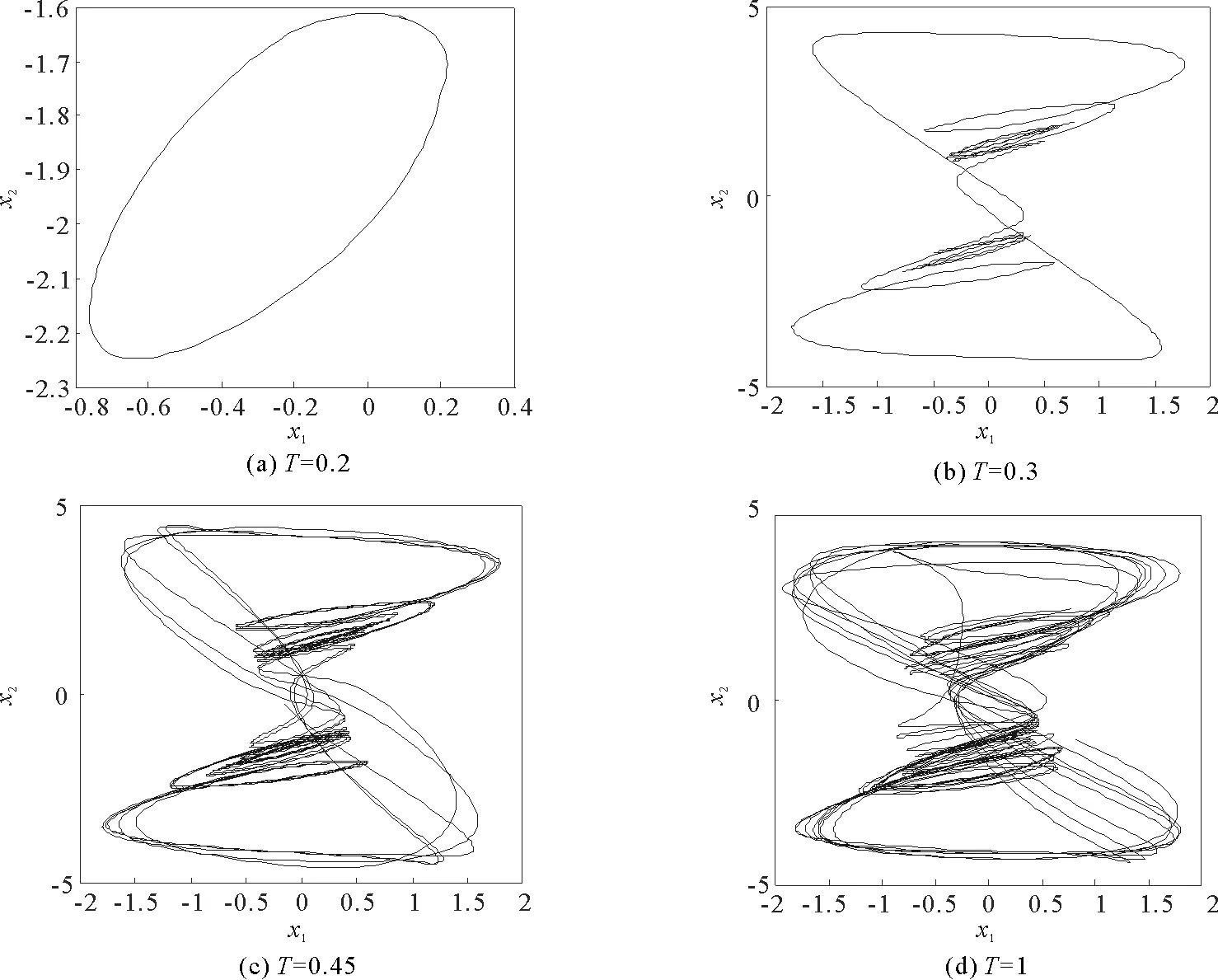
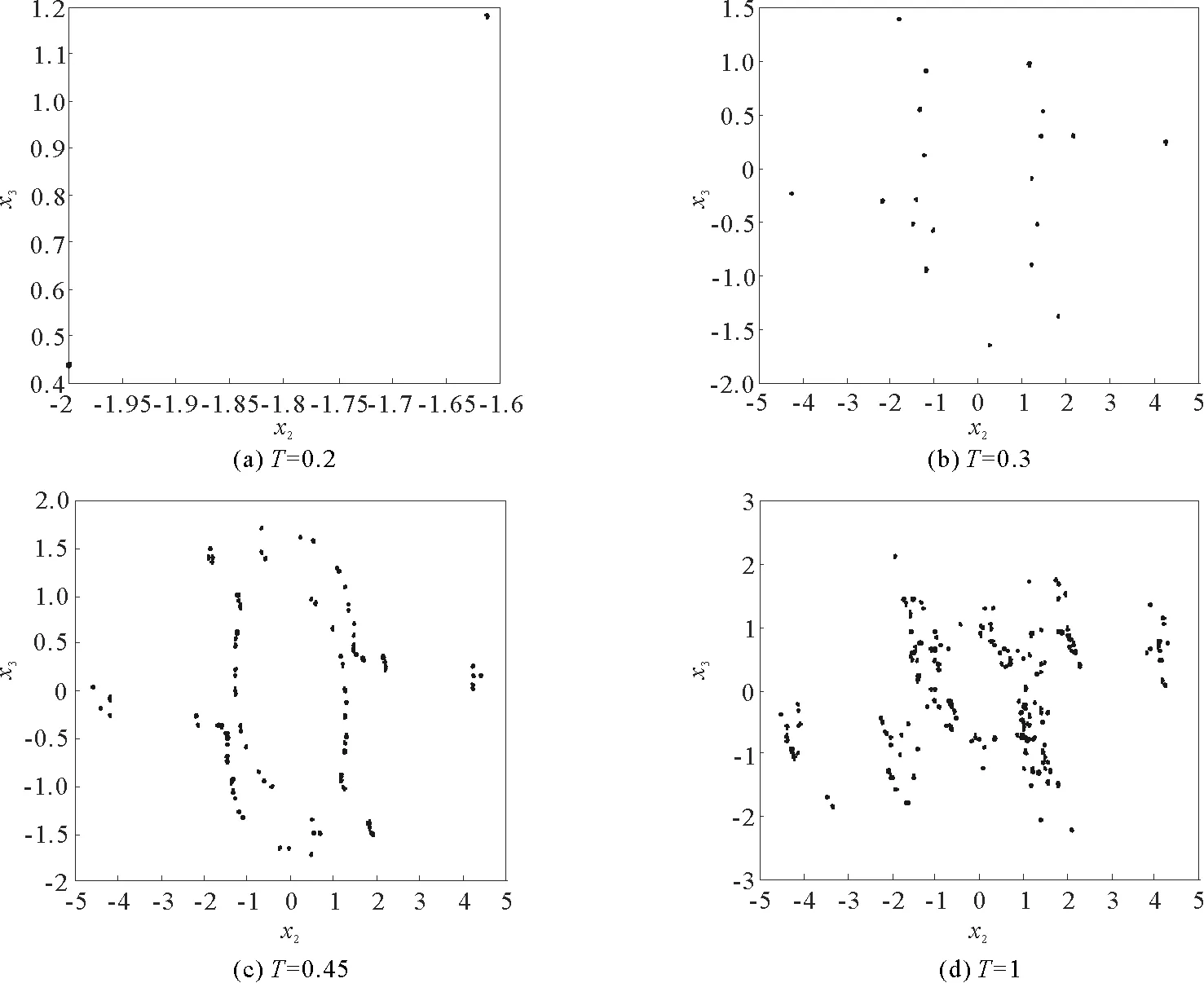
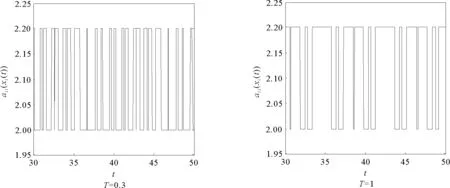
其中t≥t0,n是正整數并且滿足n-1<α 憶阻器最初被用來描述磁通φ和電荷q之間的關系。磁通φ和電荷q之間的關系可以用q-φ或φ-q平面上一條過原點的特性曲線f(φ,q)=0來表征。磁通和電荷之間的關系φ=φ(q)可以定義一個電荷控制(或電流控制)的憶阻器。此時,非線性關系f(φ,q)=0能由關于電荷q的單值方程φ=φ(q)表示出來。因此,憶阻器可以用其憶阻值M(q)來表征,其電流-電壓關系特性為 同樣地,電荷-磁通特征關系q=q(φ)能定義一個磁通控制(或電壓控制)的憶阻器。此時,f(φ,q)=0能由一個關于磁通φ的單值方程q=q(φ)來表示。由此可以推出: 考慮一類不連續時滯分數階憶阻神經網絡[14-17],表示如下: (1) 其中,i=1,2,…,n,n代表神經元的數量;0<α< 1代表分數階;ci> 0代表自反饋系數;xi(t)為第i個神經元的狀態變量;fj(·),gj(·)代表激活函數;τ代表時滯。憶阻連接系數aij(xj(t))和bij(xj(t))可以表示為: 本文提出了一個三維的不連續時滯分數階憶阻神經網絡模型,描述為 (2) 其中,將參數設置如下:c1= 2.2,c2= 1.2,c3= 1.8,τ=0.8,T= 1,fj(xj)=gj(xj)=tanh(xj),j= 1,2,3。不連續的連接權重為: 令α= 0.905,初始狀態設定為x(s)= (0.9,-0.5,0.7)T,?s∈ [-0.8,0]。如圖1所示,系統(2)能夠產生混沌吸引子。 圖1 當初始狀態x(s) = (0.9,-0.5,0.7)T時系統(2)的相圖Fig.1 Phase portraits of system (2) with initial condition x(s)= (0.9,-0.5,0.7)T 圖2 隨x10變化的分岔圖Fig.2 Bifurcation diagram with varied x10 上述分析已經驗證:當α=0.905,x(s)= (0.9,-0.5,0.7)T,T= 1時,系統處于混沌狀態。因此,取系統的初始狀態α= 0.905,T= 1,(x1,x2,x3)T= (x10,-0.5,0.7)T,x10的變化范圍為0.9~9,步長為0.02。分數階微分方程(2)通過Adams-Bashforth-Moulton 預估-校正算法[20]求解,步長為0.005。如圖2所示,當x10從0.9變化到8.12時,隨著x10的增加,系統(2)表現出混沌行為。當x10從8.14變化到9,系統(2)出現周期-1軌道。 分別選取不同的x10,系統(2)的相圖及相應的龐加萊截面(選取的截面為x1=0.5)如圖3~4所示,仿真時間范圍設為[200 s,400 s]。不同的x10對應的動力學行為如表1所示。 圖3 x10取不同值時系統(2)的相圖Fig.3 Phase portraits exhibited in system (2) with different values of x10 圖4 x10取不同值時系統(2)的龐加萊截面Fig.4 Poincaré sections of system (2) with different values of x10 表1 x10取不同值時系統(2)的動力學Tab.1 Dynamics of system (2) for different x10 圖5 隨α變化的分岔圖Fig.5 Bifurcation diagram with varied α 令初始狀態(x1,x2,x3)T=(1,-0.5, 0.7)T,T= 1。α從0.8變化到1,步長為0.000 4。如圖5所示,當α∈ [0.841 6,0.909 2],[0.910 8,0.951 6]和[0.954 0,0.951 2]時,系統(2)展現出混沌狀態。當α∈ [0.800 0, 0.841 2],[0.909 6,0.910 4],[0.952 0,0.953 6],[0.961 6,0.986 0],[0.986 4,0.993 6]和[0.994 0,1.000 0]時,系統(2)表現出周期狀態。 選取不同的分數階α,系統(2)的相圖及相應的龐加萊截面(選取的截面為x1=0)如圖6~7所示,仿真時間范圍設為[200 s,400 s]。不同的分數階α對應的動力學行為如表2所示。 圖6 α取不同值時系統(2)的相圖Fig.6 Phase portraits exhibited in system (2) with different values of α 圖7 α取不同值時系統(2)的龐加萊截面Fig.7 Poincaré sections of system (2) with different values of α 由圖2、圖5可以看出,隨著分岔參數的變化,周期窗口與混沌窗口以陣發的形式交替出現,而未出現通過倍周期分岔到混沌的這種分岔過程。因此,不同于文獻[5,11]中所研究的連續型系統的倍周期分岔,不連續系統(2)通往混沌的道路為陣發混沌。因此,本研究豐富了之前的結果。 令初始狀態(x1,x2,x3)T= (1,-0.5,0.7)T,α= 0.905。T的變化范圍為0.1~1.1,步長為0.002。當T∈ [0.392,0.544],[0.590,1.100]時,系統(2)展現出混沌狀態。當T∈[0.100,0.222],[0.224,0.390],[0.546,0.588]時,系統(2)表現出周期狀態。 選取不同的開關階躍T,系統(2)的相圖及相應的龐加萊截面(選取的截面為x1=0)如圖9~10所示,仿真時間范圍設為[200 s,400 s]。不同的開關階躍T對應的動力學行為如表3所示。 表2 α取不同值時系統 (2) 的動力學Tab.2 Dynamics of system (2) for different α 圖8 隨T變化的分岔圖Fig.8 Bifurcation diagram with varied T 圖9 T取不同值時系統(2)的相圖Fig.9 Phase portraits exhibited in system (2) with different values of T 圖10 T取不同值時系統(2)的龐加萊截面Fig.10 Poincaré sections of system (2) with different values of T T動力學圖0.20周期-1圖9(a)0.30周期-10圖9(b)0.45混沌圖9(c)1.00混沌圖9(d) 圖11 T取不同值時a11(x1(t))的切換律Fig.11 Switching laws of a11(x1(t)) with different values of T 由于不連續憶導函數的存在,使得系統(1)本質上是一個由2n個子系統構成的切換系統。顯然,新構建的系統(2)由8個子系統構成。因此,不連續憶導函數的加入可以豐富切換系統的子系統數目。特別地,本文分析了開關階躍T對系統(2)動力學行為的影響。本文憶阻器的阻值是二值切換的,當開關階躍T達到閾值電壓時,憶阻器的阻值為一個特定的值,當開關階躍T的值小于閾值電壓時,憶阻器的阻值為另一個特定的值。憶阻器的阻值在兩個值之間切換,系統展現出復雜的動力學行為。值得注意的是,不同的開關階躍T并沒有改變系統(2)的8個子系統的動力學行為,但可以改變憶阻連接權重的切換律。如圖11所示,不同的開關階躍T能夠產生不同的切換律,進而可以影響或改變系統(2)的動力學行為。 提出了一個不連續的時滯分數階憶阻神經網絡模型,通過選取不同的分岔參數,對該模型進行了詳細的分岔分析。利用分岔圖、相圖和龐加萊截面等數值仿真手段驗證了其典型的動力學行為。不同于倍周期分岔,所提出的不連續分數階憶阻神經網絡通往混沌的道路為陣發混沌。同時,還揭示了不連續的憶導函數和開關階躍T對系統動力學的內在影響機制。研究結果可為混沌生成提供新的思路和方法。1.2 憶阻器模型
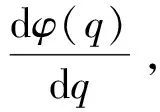
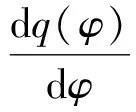
2 不連續時滯分數階憶阻神經網絡中的混沌現象
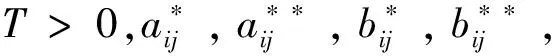
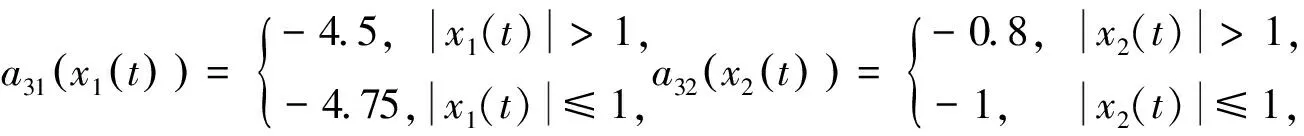
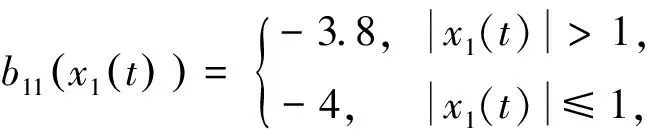
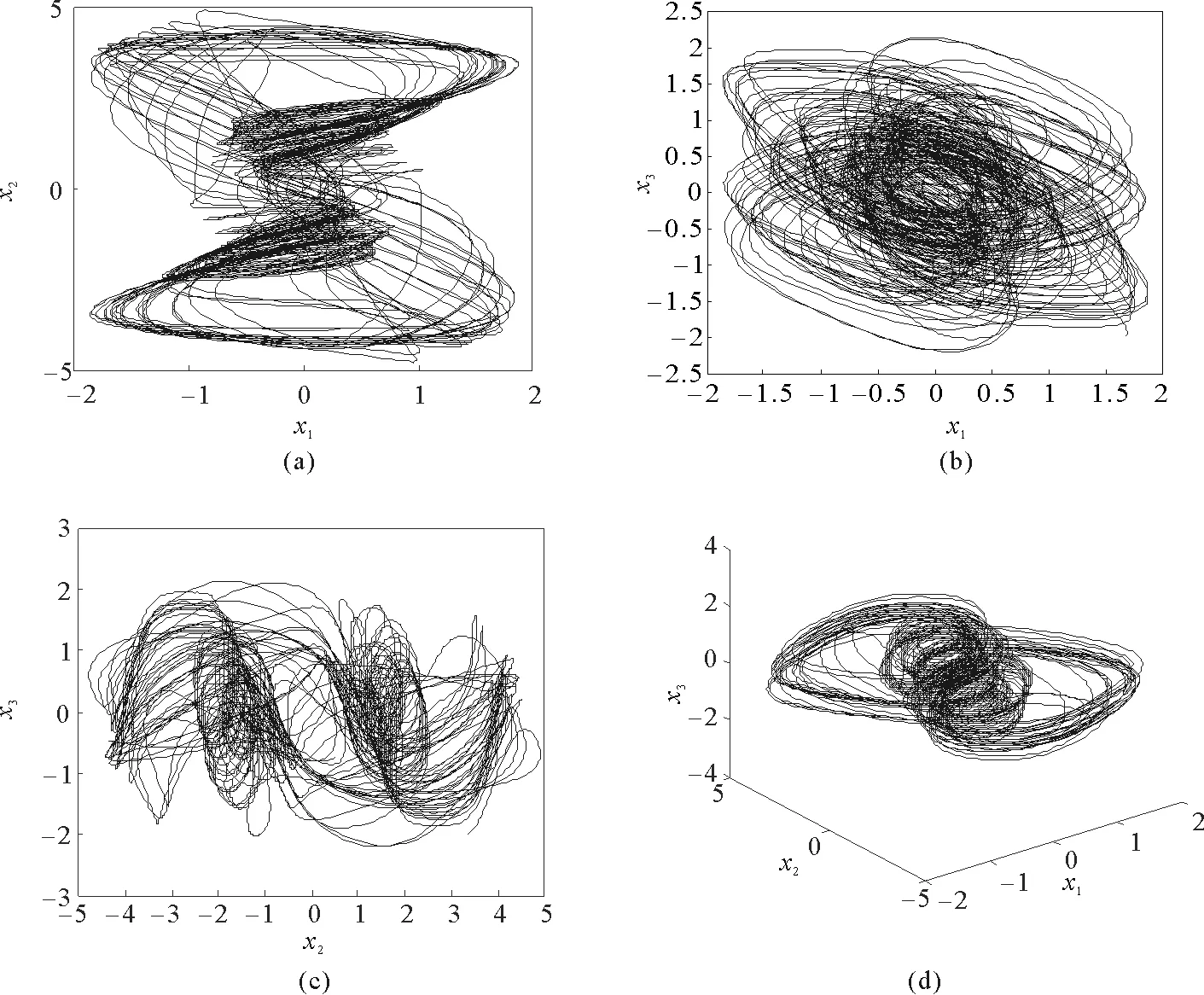
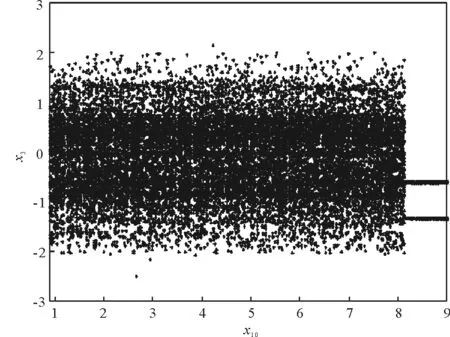
2.1 隨初值x10的分岔分析

2.2 隨分數階α的分岔分析
2.3 開關階躍T的分岔分析



3 結論

