行波旋轉型超聲波電動機定轉子接觸滑移分析

劉 炯，紀躍波

(集美大學，廈門 361021)

0 引 言

行波型超聲波電動機是利用壓電陶瓷的逆壓電效應，通過壓電陶瓷，使定子表面產生行波，進而使定子表面質點形成橢圓的運動軌跡，在一定的預壓力作用下，質點橢圓運動軌跡的切向摩擦力驅動轉子周向運動。相對于電磁電機，超聲波電動機具有轉矩質量比大、低轉速、無電磁干擾等優點，廣泛應用于醫療、航天、機器人等行業[1-3]。

由超聲波電動機的工作原理可知，定子振動時，接觸面質點的運動軌跡是空間三維的，既有橫向位移也有縱向位移和徑向位移[4]。文獻[5]通過增大定子與摩擦層間的摩擦因子和增大摩擦材料的泊松比來減小超聲波電動機定轉子間的徑向滑移。文獻[6]指出，轉子中存在一定的阻尼有利于減少徑向相對滑動造成的動力損耗，提高超聲波電動機的輸出效率。超聲波電動機定轉子之間的徑向滑移造成的能量損耗是不可忽視的，研究超聲波電動機結構對滑移大小的影響，有利于提高超聲波電動機機械效率，減小工作時造成的能量損失[7]。以上文獻都是從超聲波電動機材料方向分析對接觸面徑向滑移的影響，本文分析超聲波電動機結構對定轉子接觸表面質點間滑移距離的影響，選擇轉子腹板厚度d、定子腹板厚度k、柔性環節寬度a和柔性環節高度h四個為主要影響參數。在施加相同邊界條件下，分析定轉子結構參數變化對最大滑移距離的影響規律，減小定轉子接觸面的徑向滑移，優化電機結構，提高電機輸出效率。

1 轉子三維建模

1.1 定轉子整體結構設計

行波型超聲波電動機主要由轉子、摩擦層、定子和壓電陶瓷組成，如圖1所示。通過ANSYS進行接觸仿真分析，根據定轉子接觸表面質點最大滑移距離，分析轉子腹板厚度d、柔性部分高度h、柔性部分寬度a和定子腹板厚度k四個結構參數變化對定轉子接觸滑移的影響規律。在超聲波電動機結構設計時，為了使定子傳遞更多的能量給轉子，轉子外徑通常與定子外徑相近[8-9]，本文選取定子外徑60 mm、內徑18 mm，轉子外徑59 mm、內徑18 mm，摩擦片厚度0.5 mm，建立行波型超聲波電動機3D結構模型，如圖2所示。

(a) 定轉子剖視圖

(b) A局部放大圖

(c) B局部放大圖

圖2 定轉子3D結構模型

1.2 三維模型生成

應用有限元計算軟件ANSYS，建立超聲波電動機的接觸模型，如圖2所示，選擇三維20節點單元solid95對定轉子進行網格劃分。根據接觸面接觸對的設置方法，將定子表面設置為目標面，將摩擦層與定子接觸的下表面設置為接觸面，并設定接觸對的摩擦系數為μ=0.15。根據電機工作的實際狀況，對定子的螺釘孔進行全約束，對轉子施加徑向約束，使其不能發生平動，在轉子的上表面施加預壓力F=120 N，使定轉子充分接觸，以傳遞轉矩。由于定子上的壓電陶瓷在靜態時力的作用較小，因此，忽略考慮壓電陶瓷對接觸應力分布產生的影響。摩擦層厚度為0.5 mm，粘接在轉子表面。超聲波電動機構件的材料參數如表1所示。

表1 定轉子材料主要參數

2 分析與結果

各個部分參數選擇如表2所示，通過分析不同結構參數對滑移距離的影響規律，為超聲波電動機的優化設計提供理論基礎。

表2 電機尺寸分析選擇表

2.1 轉子腹板厚度和柔性部分寬度的影響分析

取柔性部分寬度a和轉子腹板厚度d為變量，設定柔性部分高度h=2 mm，定子腹板厚度k=0.8 mm。接觸面最大滑移距離如表3所示。

表3 不同轉子腹板厚度和柔性部分寬度對應接觸最大滑移距離(單位：mm)

其對應的變化曲線如圖3和圖4所示。

圖3 不同轉子腹板厚度下柔性部分寬度與滑移距離關系圖

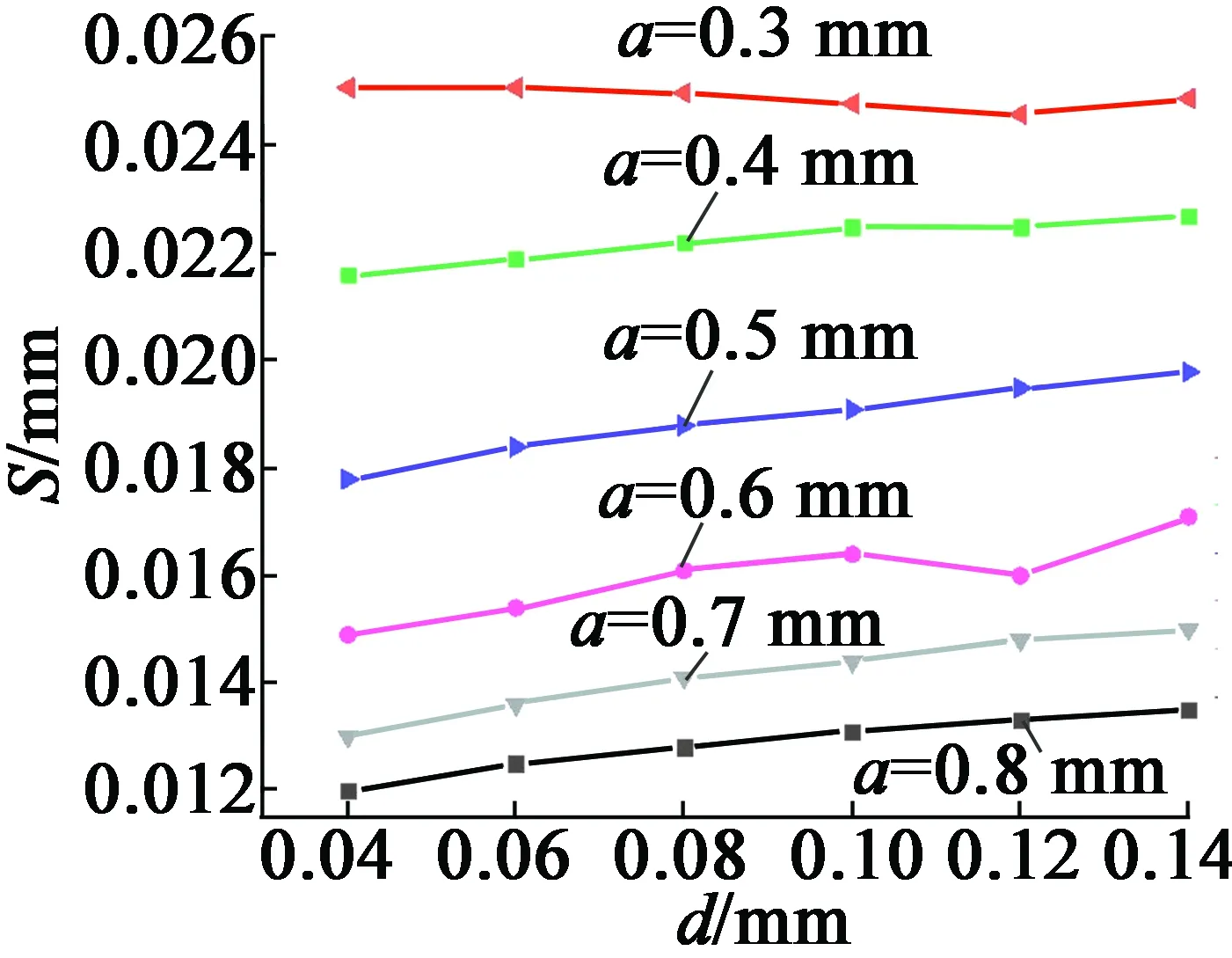
圖4 不同柔性部分寬度下轉子腹板厚度與滑移距離關系圖

由圖3可以得到，轉子腹板厚度d不變時，隨著柔性部分寬度a變大，滑移距離變小，且變化趨勢明顯；由圖4可以得到，隨著轉子腹板厚度d變大，滑移距離變化很小。由此可知，柔性環節寬度變化對滑移距離影響較大，轉子腹板厚度對滑移距離幾乎無影響。

進一步分析得到如圖5所示的在不同柔性部分寬度下接觸滑移距離的分布情況。由定子齒表面質點振動軌跡可知，在接觸區域存在徑向滑移現象。由圖5可得，柔性部分寬度變大，接觸面積減小，使接觸面磨損加劇。

圖5 柔性部分寬度變化下的接觸滑移分布圖

2.2 轉子柔性部分寬度與高度的影響分析

取柔性部分寬度a和高度h為變量，設定轉子腹板厚度d=1 mm，定子腹板厚度k=0.8 mm。接觸最大滑移距離結果如表4所示。

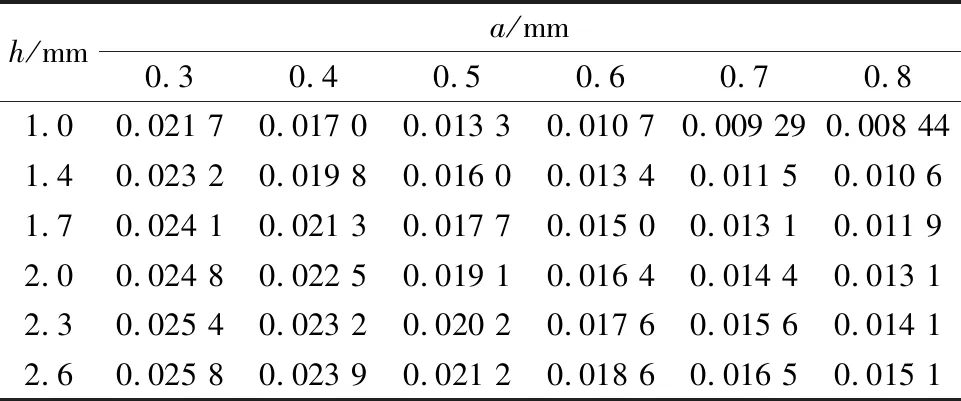
表4 不同柔性部分寬度和高度對應接觸 最大滑移距離(單位：mm)

其對應的變化曲線如圖6和圖7所示。

圖6 不同柔性部分高度下柔性部分寬度與滑移距離關系圖

圖7 不同柔性部分寬度下柔性部分高度與滑移距離關系圖

由圖6可以得到，隨著柔性部分寬度a變大，接觸滑移距離變小；由圖7可以得到，隨著轉子柔性環節高度h變大，滑移距離變大。由此可知，柔性環節寬度變化對滑移距離影響較大，柔性部分高度變化對滑移距離影響較小。

進一步分析得到如圖8所示的在不同柔性部分寬度下接觸滑移距離的分布情況。由圖8可知，柔性部分高度的變化，對定子和轉子接觸面積影響較小。

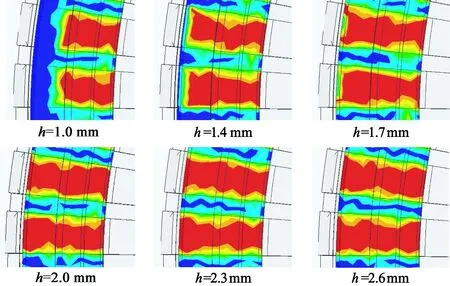
圖8 柔性部分高度變化下的接觸滑移分布圖

2.3 定子腹板厚度與柔性環節寬度的影響分析

取柔性環節寬度a和定子腹板厚度k為變量，設定轉子腹板厚度d=1.0 mm，柔性環節高度h=2.0 mm。接觸面最大接觸應力結果如表5所示。

表5 不同定子腹板厚度和柔性環節寬度 對應接觸最大滑移距離(單位：mm)

其對應的變化曲線如圖9和圖10所示。

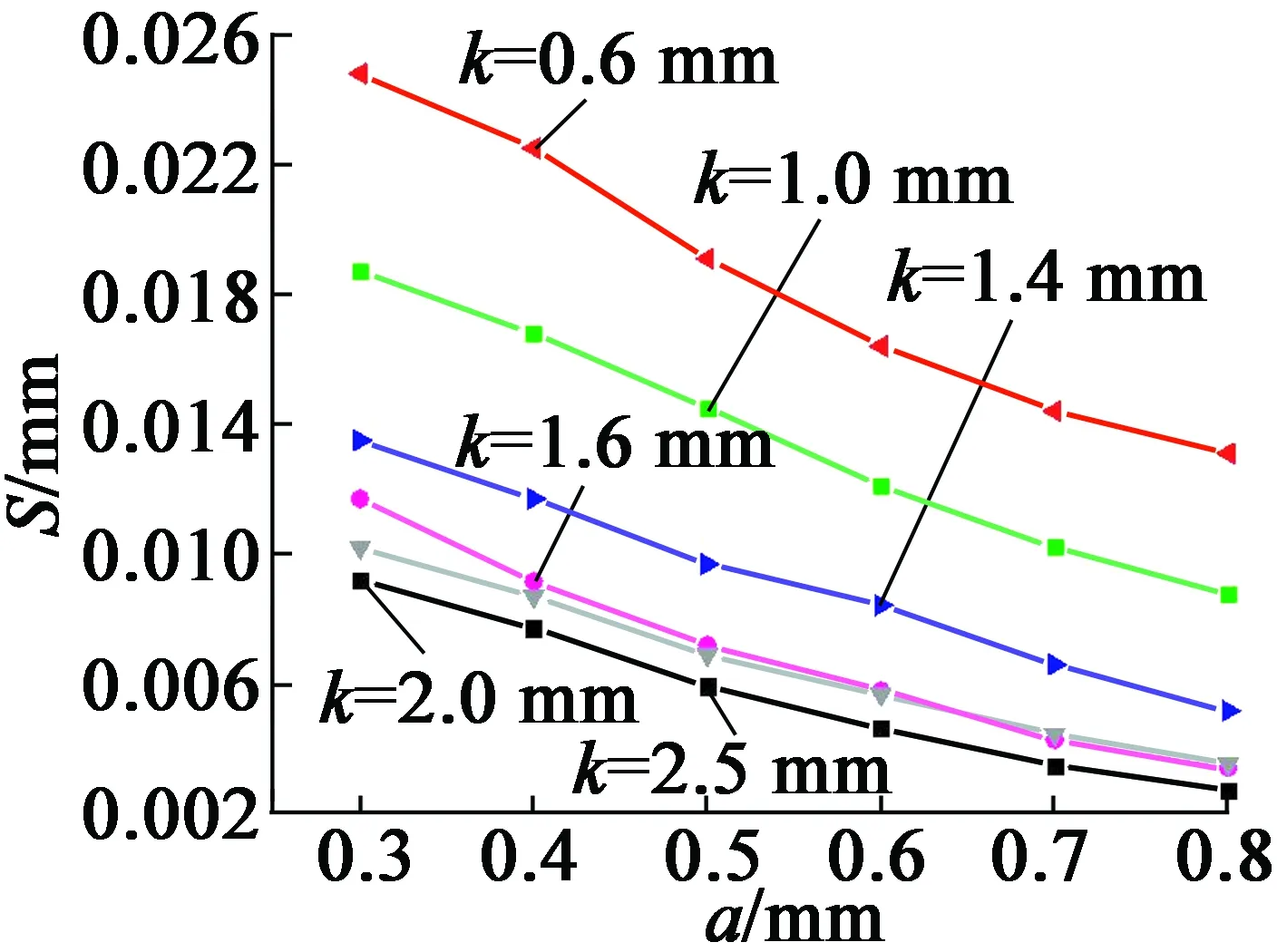
圖9 不同定子腹板厚度下柔性環節寬度與滑移距離關系圖

圖10 不同柔性環節寬度下定子腹板厚度與滑移距離關系圖

由圖9可得，定子腹板厚度不變時，柔性環節寬度變大，滑移距離變小；由圖10可得，柔性環節寬度不變時，定子腹板厚度變大，滑移距離變小，且當定子腹板厚度增大到一定時，滑移距離變化量逐漸減小。由此可知，定子腹板厚度變化對滑移距離影響較大。

進一步分析得到如圖11所示的在不同柔性部分寬度下接觸滑移距離的分布情況。由圖11可知，定子腹板厚度變大，接觸面積先減小后變大。

3 結 語

本文根據對超聲波電動機整體結構四個尺寸參數在相同邊界條件下對接觸滑移距離的仿真分析，可以得出：電機轉子腹板厚度d的變化對接觸面滑移距離幾乎無影響；柔性環節高度h對接觸滑移距離影響較小，柔性環節高度越大，滑移距離越大；柔性環節寬度對接觸面滑移距離影響較大，且柔性環節寬度越大，滑移距離越小；定子腹板厚度對接觸面滑移距離影響最大，定子腹板厚度越大，滑移距離越小。柔性部分寬度和定子腹板厚度對定子和轉子接觸面積影響較大。故在設計時結合超聲波電動機定轉子結構對接觸面滑移距離影響規律，合理選擇結構參數，提高超聲波電動機輸出效率。