水利工程應急方案直覺模糊多屬性決策研究

馬文俊，孫開暢，顏 鑫，李 權

(1.三峽大學水利與環境學院，湖北宜昌443002；2.湖北能源集團溇水水電有限公司，湖北恩施445000)

水利水電工程施工安全生產活動由于受人、機、環境和管理等因素影響，安全事故時有發生，努力降低事故發生的可能性顯得極為重要[1]。針對水利工程事故的發生，事故的應急方案決策是重要的風險控制途徑，對提升水利工程應急救援能力、預防和減小事故不良后果具有重要的意義[2-3]。目前對應急方案決策的研究主要包括：江新等[4]運用云決策模型建立了水電工程突發事件應急決策方法；王毅等[5]建立了直覺模糊集的多屬性決策模型，通過比較各方案的直覺模糊集與正、負理想方案的距離來確定方案集的排序；馬齊飛揚等[6]設計多agent應急救援組織結構，建立了基于改進的TOPSIS的應急救援決策方法；張超等[7]提出基于三維GIS的火電廠應急救援決策支持系統，對情景進行虛擬現實仿真。本文根據水利工程施工特點，建立應急救援方案的評價指標體系，基于直覺模糊交叉熵距離和灰色關聯分析對應急方案進行排序，并做了擾動分析來驗證模型的可靠性，以期豐富和發展水利工程應急方案決策理論。

1 直覺模糊集

直覺模糊集[8]是對Zadeh模糊集的一種擴充，相比Zadeh模糊集單一的隸屬度只能表示支持和反對兩種狀態，直覺模糊集同時考慮隸屬度和非隸屬度兩方面的信息，表達了模糊概念支持、反對和中立三種狀態，使得直覺模糊集在處理不確定性信息時有更強的表述和推理能力。

定義：對于非空集合X=(x1，x2，…，xn)，設A為論域X上的直覺模糊子集A∈IFS(X)，A={〈x，μA(x)，γA(x)〉x∈X}，其中μA(x):X→[0，1]和γA(x):X→[0，1]分別為X上元素x屬于A的隸屬度函數和非隸屬度函數，x∈X，滿足0≤μA(x)+γA(x)≤1。πA(x)=1-μA(x)-γA(x)為直覺模糊集A中x的直覺指數，表示元素x屬于集合A的猶豫度，對任意x∈X，滿足0≤πA(x)≤1。若另有一與A形式相同的論域X上直覺模糊子集為B={〈x，μB(x)，γB(x)〉x∈X}，πB(x)=1-μB(x)-γB(x)，則直覺模糊集A和B之間的直覺模糊交叉熵[9]為

CE(A，B)=∑ni=1{[1+μA(xi)-vA(xi)/2]×

log2[1+μA(xi)-vA(xi)]/12[(1+μA(xi)-

vA(xi))+(1+μB(xi)-vB(xi))]}+

∑ni=1{[1-μA(xi)+vA(xi)]/2×log2[1-

μA(xi)+vA(xi)]/12[(1-μA(xi)+vA(xi))+

(1-μB(xi)+vB(xi))]}

(1)

由于直覺模糊交叉熵CE(A，B)不滿足對稱性，故令

CE*(A，B)=CE(A，B)+CE(B，A)

(2)

式中，CE*(A，B)為直覺模糊交叉熵的改進形式，并將其定義為直覺模糊交叉熵距離。

2 IAHP-直覺模糊交叉熵決策模型

設有m個可供選擇的應急救援方案組成方案集Ai=(A1，A2，…，Am)，每個方案有n個屬性組成屬性集Bj=(B1，B2，…，Bn)。在信息不完全確定的模糊環境下，備選方案的主觀偏好值用Oi=(αi，βi)表示，方案Ai的第j個指標評價值用直覺模糊集Fij=(μij，γij)表示。μij和γij分別表示決策方案Ai對屬性Bj的滿足程度和不滿足程度，μij，γij∈[0，1]且0≤μij+γij≤1。

結合灰色關聯分析法[10-11]，計算基于直覺模糊交叉熵距離的各備選方案主觀評價值相對于決策者主觀偏好值的灰色關聯度系數

γij=miniminjCE*ij+ξmaximaxjCE*ijCE*ij+ξmaximaxjCE*ij

(3)

式中，ξ為灰色分辨系數，通常其取值在0和1之間，一般取0.5。此處的灰色關聯度系數表明在屬性Bj的條件下，決策者對備選方案Ai的主觀評價值相對于主觀偏好值的接近程度。

令評價指標權重值為ωjj=1，2，…，n，可得出各備選方案Ai在所有屬性條件下的綜合灰色關聯度系數

γi=∑nj=1γijωj

(4)

式中，0≤ωj≤1，∑nj=1ωj=1。根據各備選方案的綜合灰色關聯度系數γi進行排序，γi越大，方案越優。

在水利水電工程實際施工過程中，安全事故的發生具有一定的突發性。由于專家判斷信息的局限性和客觀情景的復雜性，評價指標權重往往難以明確。IAHP是對層次分析法進行改進，通過用區間數代替判斷點值構成判斷矩陣并求區間數權重，能有效反映判斷的不確定性，大大減小人為主觀判斷的影響[12-13]。

參照指標層次結構，采用互反性1～9標度對層次結構中的指標進行區間標量化判斷，構造區間判斷矩陣。若實數a為一個區間數且a=[a-，a+]，則指標的區間判斷矩陣表示為A=(aij)n×n。其中，aij=[a-ij，a+ij]表示指標i相對指標j的重要程度。

專家對指標進行兩兩比較和判斷取值過程中，可能出現不一致或自相矛盾的結果，這時判斷信息的可靠性降低，影響最終權重計算的準確性，因此需對區間判斷矩陣進行一致性檢驗。若不滿足一致性檢驗，則運用一致性修正算法進行校正或讓專家重新進行判斷取值。一致性檢驗方法如下[14]

k=∑nj=11∑ni=1a+ij，β=∑nj=11∑ni=1a-ij

(5)

當k≤1且β≥1時，判斷矩陣具有良好的一致性；當k>1或β<1時，判斷舉證一致性較差。

設A-=(a-ij)n×n，A+=(a+ij)n×n，則A=[A-，A+]。利用特征根法求矩陣A-和A+的權重向量，分別為x-=(x-1，x-2，…，x-n)和x+=(x+1，x+2，…，x+n)；則各層次指標的相對權重向量表示為m(At)=(w1，w2，…，wn)，計算公式如下[15]

m(At)=12(kx-+βx+)

(6)

此時m(At)中各指標權重的和并不為1，對m(At)歸一化處理后獲得最終指標權重向量w=(w1，w2，…，wn)。最后可根據灰色關聯分辨系數的ξ取值變化做擾動分析，以此來檢驗決策模型的穩定性和可靠性。

3 實例分析

某水電站進行右岸二道壩下游至尾水洞出口段貼坡混凝土澆筑作業過程中，在準備收倉時，上游側面模板突然發生爆模，整倉混凝土從爆模處涌至正在備倉的混凝土倉面，導致該混凝土倉面靠下游的正面模板被沖垮，造成了混凝土坍塌事故，事故造成重大的人員傷亡。事故發生后，工程項目部立即啟動生產安全應急救援預案。經初步判斷迅速制定A1，A2，A3，A44套應急救援方案，現應用本文提出的決策模型對應急方案進行決策分析。

在坍塌救援過程中，一方面從技術因素的角度考慮，首先要對災害現場進行有效的控制，對于爆模周邊單元模板支撐要進行必要的檢查加固，防止救援過程中再次出現坍塌事故；水利工程施工場地的應急救援應根據實際情況來考慮機械設備的利用，選擇合適的機械來進行救援；并且還要考慮救援時效性，妥善處理救援過程中發生的各種意外事件。另一方面從社會影響的角度來考慮，對于事故災害善后和所造成的社會影響必須深思熟慮，全面了解后盡最大努力降低災害所造成的社會影響，減少損失，并引以為戒。綜合考慮水利工程施工作業和應急救援的特點，選取如下若干因素作為決策方案的影響指標，對相應的急救援方案進行評價，建立水利工程應急決策層次結構如圖1所示。

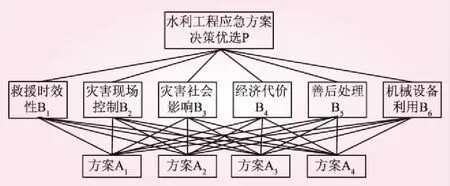
圖1 水利工程應急決策層次結構

專家通過知識、經驗和統計數據對評價指標進行判斷，集合各個專家的意見，根據IAHP得到評價指標與目標形成的區間判斷矩陣，如表1所示。

對矩陣進行一致性檢驗，根據由式(5)可得：k=0.863 8，β=1.055 4，k≤1且β≥1，判斷矩陣具有良好的一致性。運用特征根法，歸一化處理后得評價指標的權重為wB=(0.365 7，0.179 0，0.222 7，0.097 1，0.090 6，0.044 7)。專家根據6個評價指標，對4個應急救援方案進行分析并給出隸屬度和非隸屬度值，形成直覺模糊集決策矩陣F=[(μij，γij)]，如表2所示。

專家對方案Ai的主觀偏好值用直覺模糊數表示，分別為：O1=(0.6，0.3)，O2=(0.7，0.2)，O3=(0.5，0.3)，O4=(0.3，0.4)。據公式(1)～(3)計算各備選方案主觀評價值相對于決策者主觀好值的直覺模糊交叉熵距離，構成距離矩陣CE*和取灰色分辨系數ξ為0.5計算所得灰色關聯度系數矩陣如下

CE*ij=

0.041 100.003 80.017 20.004 10.131 9

0.004 50.022 70.017 20.017 20.064 10.097 6

0.003 80.037 20.003 80.003 80.003 70.003 7

0.032 70.483 40.032 70.015 10.003 60.032 7

γij=

0.854 71.000 00.984 50.933 60.983 30.646 9

0.981 70.914 10.933 60.933 60.790 40.712 3

0.984 50.866 60.984 50.984 50.984 90.984 9

0.880 80.333 30.880 80.941 20.985 30.880 8

指標權重帶入式(4)得綜合灰色關聯度系數矩陣γi=(0.919 50.924 70.963 30.798 0)。根據各備選方案的綜合灰色關聯度系數進行排序，系數越大，方案越優，故備選方案排序為A3>A2>A1>A4，即最優方案為A3方案。

分別取灰色分辨系數數ξ為0.10，0.20，0.35，0.50，0.65，0.80，0.95，對決策模型進行擾動分析，各備選方案的綜合灰色關聯度系數及方案排序如表3所示。

從表3可以看出，應急預案的排序結果基本并未隨著灰色分辨系數的變化而變化，只在分辨系數取0.10時出現了一定的排序變化，但最優方案仍與其他情況相同為A3方案。這也說明決策結果相對穩定，權重設置比較合理，決策模型表現出了一定的可靠性和穩定性。

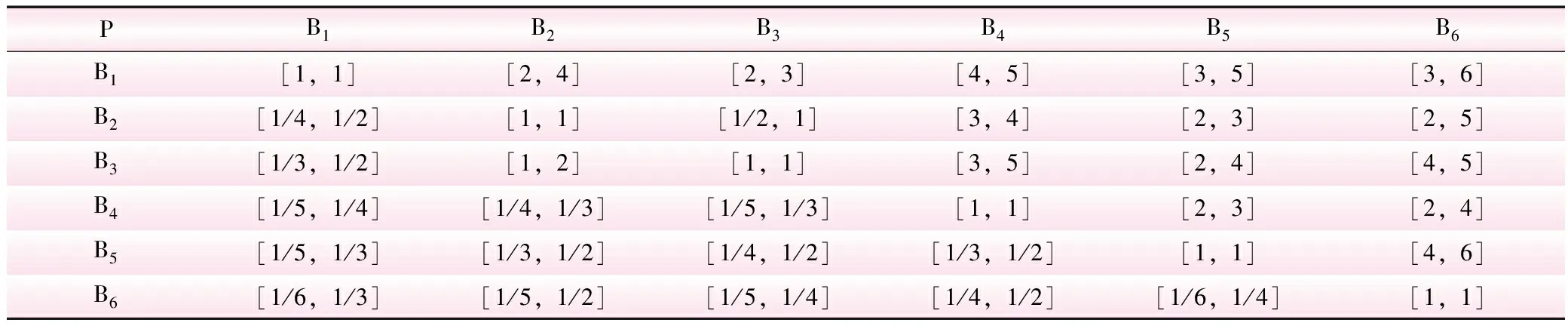
表1 區間判斷矩陣

表2 直覺模糊決策矩陣

表3 不同灰色分辨率下的決策結果

4 結 論

(1)通過對水利工程施工的特點和安全生產現場的分析，識別出對水利工程應急救援有重大影響的評價指標因素，提出基于IAHP-直覺模糊交叉熵的決策方法，構建了水利工程應急救援方案決策模型。

(2)在確定應急救援方案評價指標體系的基礎上，IAHP通過區間數替代確定值構建判斷矩陣，能有效避免主觀判斷的影響，獲取更真實的指標權重；用直覺模糊交叉熵替代傳統的直覺模糊數距離測度公式，能更有效、真實的測度評價信息，規避了無法比較大小或信息混淆的情況；最后通過灰色關聯度系數大小進行合理排序，很好地加強了模型決策的準確性。

(3)對決策模型進行擾動分析，驗證了決策模型具有一定的可靠性和穩定性。該模型也可以應用到其他多屬性決策問題，具有較好的適用性和推廣性。