三角函數常見典型考題賞析

■黃林平

三角函數是高中數學的基礎知識之一，同學們要理解其定義，掌握三角公式的靈活運用。下面就三角函數常見的典型考題進行舉例剖析，供大家學習與提高。

題型1：角的集合表示及象限角的判斷

利用終邊相同的角的集合可以求適合某些條件的角，方法是先寫出與這個角的終邊相同的所有角的集合，然后通過對集合中的參數賦值來求得所需角。利用終邊相同的角的集合S=｛β|β=2kπ+α，k∈Z｝判斷一個角β所在的象限時，只需把這個角寫成[0，2π）范圍內的一個角α與2π的整數倍的和，然后判斷角α所在的象限。

例1集合中的角所表示的范圍（陰影部分）是（ ）。

解：當k=2n（n∈Z）時此時α表示的范圍與表示的范圍一樣；當k=2n+1（n∈Z）時，2nπ此時α表示的范圍與表示的范圍一樣。應選C。

跟蹤訓練1：點A（sin2018°，cos2018°）在直角坐標平面上位于（ ）。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

提示：由sin2018°=sin218°=-sin38°＜0，cos2018°=cos218°=-cos38°＜0，可知點A（sin2018°，cos2018°）在第三象限。應選C。

題型2：扇形的弧長、面積公式的應用

例2一個半徑為R的扇形，它的周長為4R，則這個扇形所含弓形的面積是（ ）。

D.R2（1-sin1·cos1）

解：設圓心角為θ。

跟蹤訓練2：如圖1，已知扇形OAB和OA1B1，A1為OA的中點，若扇形OA1B1的面積為1，則扇形OAB的面積為_____________。

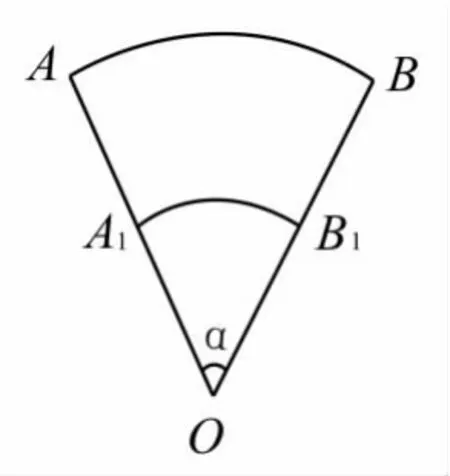
圖1

提 示：設 ∠AOB=α，則

因 為 OA=2OA1，所 以 S扇形OAB=

題型3：三角函數的定義問題

三角函數定義問題的常見類型及解題策略：（1）已知角α的某個三角函數值，求角α終邊上一點P的坐標中的參數值，可根據定義中的兩個量列方程求參數的值。（2）已知一個角的三角函數值（sinα，cosα，tanα）中任意兩個的符號，可分別確定出角終邊所在的可能位置，兩者的交集即為該角終邊的位置，這時要注意終邊在坐標軸上的特殊情況。

例3若角α的終邊在直線3x+4y=0上，求sinα，cosα和tanα的值。

解：對于含有參數的三角函數求值問題，一定要考慮運用分類討論的思想方法。

設α終邊上任一點為P（-4a，3a）。

跟蹤訓練3：已知角α的終邊經過點P（x，且求的值。

題型4：關于sinα，cosα的齊次式問題

形如asinα+bcosα和asin2α+bsinα·cosα+ccos2α的式子分別稱為關于sinα，cosα的一次齊次式和二次齊次式。對于涉及它們的三角變換問題，通常轉化為正切值（分子、分母同除以cosα或cos2α）求解。

例4已知

（1）求sinx-cosx 的值。

解：（1）（方法1）由題意可得方程組

消去sinx后整理可得25cos2x-5cosx-12=0。因 為所以可得

跟蹤訓練4：已知sinαcos則cosα-sinα的值為（ ）。

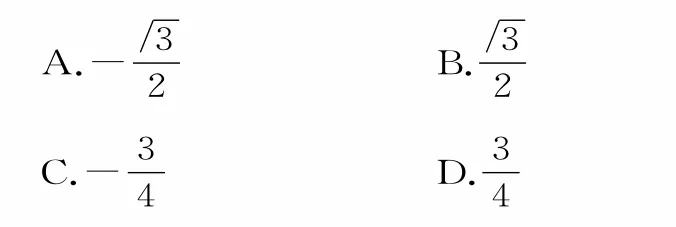
提示：由可得cosα＜0，sinα＜0，且|cosα|＜|sinα|，所以cosα-sinα＞0。又（cosα-sinα）2=1-2sinαcosα=1-2所以cosα-sinα=應選B。

題型5：三角函數的奇偶性、周期性和對稱性問題

例5已知函數f（x）=sin（ωx+φ）的最小正周期為4π，且對?x∈R，有恒成立，則f（x）圖像的一個對稱中心是（ ）。

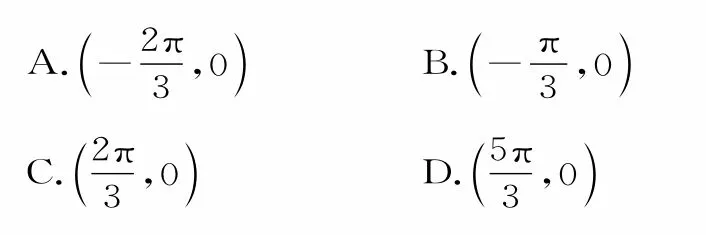
解：由f（x）=sin（ωx+φ）的最小正周期為4π，可得因為恒成立，所以即+2kπ（k∈Z）。由可得故

跟蹤訓練5：已知函數f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）為奇函數，該函數的部分圖像如圖2所示，三角形EFG是邊長為2的等邊三角形，則f（1）的值為（ ）。

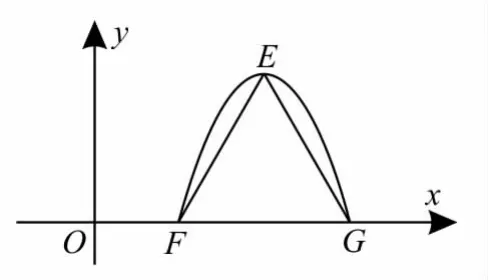
圖2

提示：由f（x）=Acos（ωx+φ）為奇函數，可得f（0）=Acosφ=0。因為0＜φ＜π，所以這時f（x）=-Asinωx。

題型6：三角函數的單調性與最值問題

求形如y=Asin（ωx+φ）+k的單調區間時，只需把ωx+φ看作一個整體代入y=sinx的相應單調區間即可（若ω為負數，則要先把ω化為正數再代入）。求較為復雜的三角函數的單調區間時，先化簡成y=Asin（ωx+φ）的形式，再求y=Asin（ωx+φ）的單調區間。

例6函數[-2π，2π]的單調遞增區間是（ ）。

B

解：依題意可得當即時，函數y=是單調遞增函數。由于x∈[-2π，2π]，因此函數的 單 調 遞 增 區 間 是應選D。

跟蹤訓練6：設ω是正實數，函數f（x）=2cosωx在上是減函數，那么ω的值可以是（ ）。

提示：因為函數f（x）=2cosωx 在上單調遞減，所以要使函數f（x）=2cosωx（ω＞0）在區間上單調遞減，則即所以解得故ω的值可以是應選A。

題型7：“五點法”作圖及圖像變換

函數y=Asin（ωx+φ）（A＞0，ω＞0）的圖像作法：（1）用“五點法”作y=Asin（ωx+φ）的圖像，可設z=ωx+φ，由z取來求出相應的x值，通過列表，計算得出五點坐標，描點后得出圖像。（2）由函數y=sinx的圖像通過變換得到y=Asin（ωx+φ）的圖像，有兩種主要途徑，即“先平移后伸縮”與“先伸縮后平移”。

例7已知曲線C1：y=cosx，C2：y=則下面結論正確的是（ ）。

A.把C1上各點的橫坐標伸長到原來的2倍，縱坐標不變，再把得到的曲線向右平移個單位長度，得到曲線C2

B.把C1上各點的橫坐標伸長到原來的2倍，縱坐標不變，再把得到的曲線向左平移個單位長度，得到曲線C2

C.把C1上各點的橫坐標縮短到原來的縱坐標不變，再把得到的曲線向右平移個單位長度，得到曲線C2

D.把C1上各點的橫坐標縮短到原來的縱坐標不變，再把得到的曲線向左平移

個單位長度，得到曲線C2

解：y=sin由y=cosx的圖像得到y=cos2x的圖像，需將曲線C1上各點的橫坐標縮短到原來的縱坐標不變；由y=cos2x的圖像得到的圖像，需將y=cos2x的圖像上的各點向左平移個單位長度。應選D。

跟蹤訓練7：將函數f（x）=-cos2x的圖像向右平移個單位后得到函數g（x）的圖像，則函數g（x）（ ）。

題型8：利用圖像求解析式y=Asin（ωx+φ）+B（A＞0，ω＞0）的方法

例8已知函數y=Asin（ωx+φ）+b的最大值為4，最小值為0，最小正周期為直線是其圖像的一條對稱軸，則下面各式中符合條件的解析式為（ ）。

解：由函數y=Asin（ωx+φ）+b的最大值為4，最小值為0，可知b=2，A=2。由函數的最小正周期為可知得ω=4。由直線是其圖像的一條對稱軸，可知即可得φ=故滿足題意的函數為2。應選D。

跟蹤訓練8：函數f（x）=2sin（ωx+φ）的部分圖像如圖3所示，則ω，φ的值分別是（ ）。

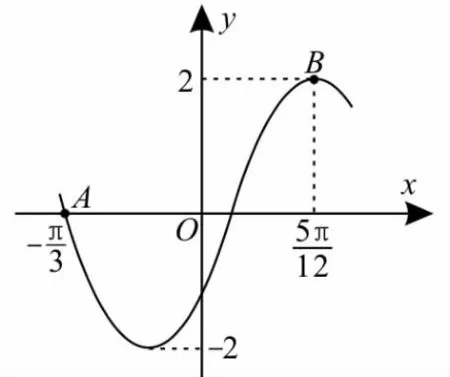
圖3

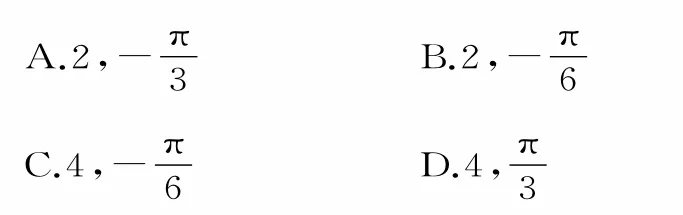
提示：由題意及圖像可知可得T=π，所以ω=2。因為圖像過點所以Z），即又所以應選A。