一題多解“再歸一”，教學設計“重變式”
——以F市一道九年級圓的綜合題研習為例

☉江蘇省江陰實驗中學 薛春燕

各地期末試題出來之后，一些網站、QQ群里都會第一時間轉發一些精品試卷，特別是對試卷中一些原創“把關題”（位于試卷中最后位置的較難題）進行求解、研習，筆者恰在某群里，發現大家對F市九年級試卷中一道與圓有關的綜合題的解法進行了探究，說法不一，有些認為試題設計巧妙，鋪墊恰當，也有教師認為從其他路徑運算繁雜，不是好題.本文就先引出這道考題，再跟進反思并給出教學設計，供研討.

一、考題及思路突破

考題：（2019年1月F市九上期末卷）如圖1，AB、AC是⊙O的弦，過點C作CE⊥AB于點D，交⊙O于點E，過點B作BF⊥AC于點F，交CE于點G，連接BE.

（1）求證：BE=BG；

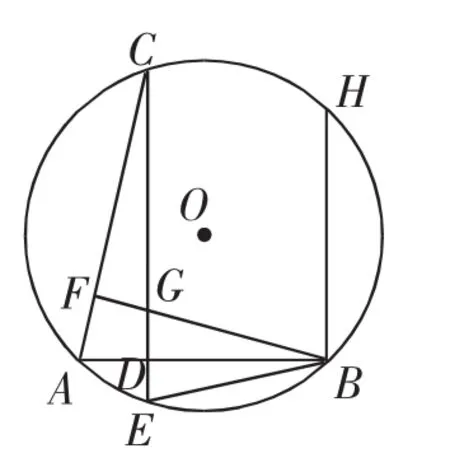
圖1

（2）過點B作BH⊥AB交⊙O于點H，若BE的長等于半徑，BH=4，AC=2，求CE（的長.

思路突破：（1）由同弧所對圓周角相等，可得∠BAC=∠BEC.結合垂直的條件，可得∠BFA=∠BDG=∠BDE=90°.∠ABF=∠ABE，于是∠BGD=∠BEC（等角的余角相等），從而BE=BG.

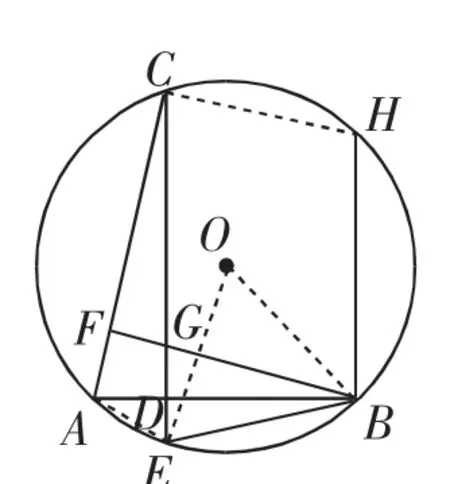
圖2

（2）如圖2，連接OB、OE、AE、CH.由四邊形ABHC內接于⊙O，可得對角互補，即∠ACH+∠ABH=180°，于是∠ACH=90°=∠AFB，從而可 得 BF∥CH.由 BH⊥AB，得∠ABH=90°=∠BDE，則BH∥CD.于是可確認四邊形BGCH是平行四邊形，則CG=BH=4.由BE=OB=OE，得△OBE是等邊三角形，則∠BOE=60°.所以∠BAE=∠BOE=30°. 在Rt△ADE中，DE=AE.設DE=x，則AE=2x.由（1）得BE=BG，結合AB⊥CD，則DG=DE=x，CD=x+4. 在Rt△ADE中，AD=x. 在Rt△ADC中，AD2+CD2=AC2，即（x）2+（x+4）2=（2）2，解得x1=1，x2=-3＜0（舍去），所以DG=1，CE=CG+GD+DE=6.

回顧反思：這道考題真正的難點在第（2）問，線段相對較多，找準突破的解題方向或目標圖形是關鍵.上面的解法，解題思路是先發現四邊形BGCH是平行四邊形，瞄準Rt△ADC，從而構造方程，成功求解.上述解法運算量不大.以下再給出一種思路，運算量偏大，但有利于我們看清這道問題的基本結構.

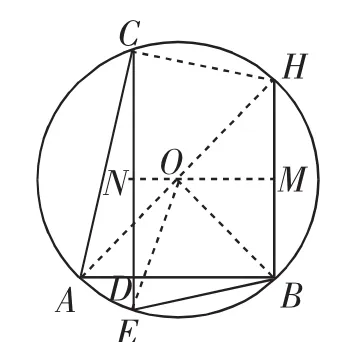
圖3

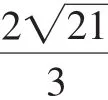
上述解法在圖3中理解起來顯得較為繁雜，事實上可以刪減無關線條，適當簡化為以下問題：

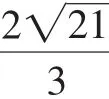
這樣以上求解就可發揮作用了.

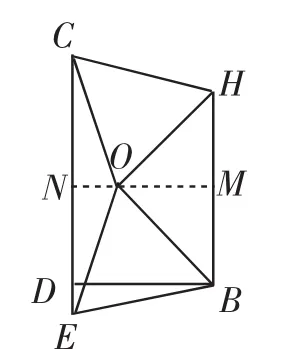
圖4

命題商榷：從這道考題的不同解法來看，找準原考題的思路，運算量不大，但是如果走向了其他方向，則運算繁雜，且數據不太“友好”，容易中途放棄繁雜數據，值得命題者慎重打磨這類問題.

二、以考題為例的解題教學設計

三、進一步的思考

例題呈現：題略，見上文“考題”.

教學組織：學生獨立思考5分鐘后，應該可以安排學生交流解法或思路進展.半數學生應該能解決第（1）問，但第（2）問很難在這么短的時間內貫通思路.這時可“訪談”優秀學生：你們有哪些思路方向，或進展如何？并預設如下一些鋪墊式問題：

鋪墊問題1：由條件“BE的長等于半徑”能解讀出哪些信息？（預設：連接OB、OE，可得△BOE是等邊三角形，所對圓周角都是30°等，再如連接CH、AH后，可得△ACH是含30°角的特殊直角三角形，等等）

鋪墊問題2：由條件“BH⊥AB”能解讀出哪些信息？（預設：連接AH，可確認AH為圓的直徑，連接CH后，可由直徑所對圓周角為直角，知∠ACH為直角）

鋪墊問題3：四邊形BHCG的形狀有什么特殊之處嗎？（預設：是平行四邊形）

鋪墊問題4：連接AE，得到的直角三角形ADE有什么特殊之處嗎？（預設：該直角三角形是含30°的特殊直角三角形）

例題變式：如圖5所示是有公共頂點C的兩個等邊三角形ABC、CDE，連接AE、BD，得到四邊形ABDE.

（1）判斷四邊形AEBD的對邊AE與BD的位置關系，并說明理由；

預設：AE∥BD.如圖6，過點C作CG⊥AE，垂足為G，交BD于H點.在△ACE中，先由“三線合一”證出∠ACG=∠ECG，進一步導角，得∠BCH=∠DCH，從而由“三線合一”可證得CH也是BD邊上的高，于是AE∥BD.

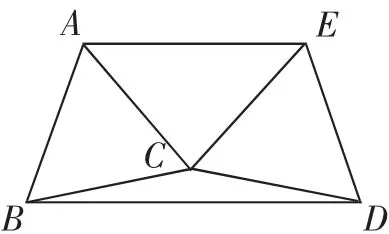
圖5

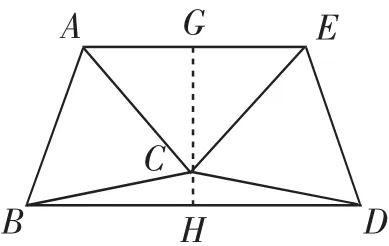
圖6

預設：由特殊數據可得∠ACE=120°，從而有∠BCD=120°，從而確認BD=.

預設：由特殊數據可得∠ACE=90°，從而有∠CBD=15°，于是把目光聚焦在直角三角形BCH中，構造圖形可得BH的長，進一步求出BD的長.

預設：聰明的學生應該發現，這組數據使得運算很繁雜，但正是考題第（2）問的“問題結構”.

1.教師解題要從一題多解走向多解歸一

教師解題需要思考思路的自然、合理，能否回到定義去解題，同時要嘗試從不同角度去攻克、貫通解題思路，也就是先要追求一題多解，而不是單一路徑、狹窄通道貫通思路.對于幾何題，特別要注意一題多解的解題追求.在一題多解的基礎上，還要思考不同解法“殊途何以同歸”，想清不同解法之間的聯系，條件之間的相通、等價等聯系和對應，這樣就達到了對問題本身的深刻理解，為后續解題教學提供了必要的備課保障.在上課、聽課過程中，有時會發現教師對有些學生的解法難以理解，或簡單干預、打斷、忽略處理，說到底，都是課前教師本人對問題的“一題多解”做得還不夠.

2.回顧反思要揭示問題結構和呈現順序

解題研究一個重要環節是回顧反思.在這個階段，要重視揭示問題的深層結構，并思考問題條件呈現的“序”.具體來說，上文考題第（2）問的深層結構就是后面我們在解題教學設計中提供的“例題變式”.而條件呈現的“序”也是非常重要的，有助于我們重新認識問題中的眾多條件是如何漸次出現的，很多情況下，解題經驗與教學經驗表明，若畫出的幾何圖形嚴重不準，都是因為對條件呈現的“序”辨識不清、理解不深，如果想清條件、線段是怎樣一步步漸次呈現的，則圖形往往會比較精準.

3.解題教學注重為學生預設鋪墊式問題

解題教學時就題講題往往“入寶山而空返”，回顧反思之后，能提供一些問題的深層結構，再小結一些解題策略或模型積累，往往能幫助優秀學生提高“模式識別”能力.但要幫助更多學生真正理解問題，以便達到“解一題、會一類”的效果，還是需要我們精心備課，深入構思，預設出系列鋪墊式問題，從而幫助更多學生弄懂、弄深、弄透問題，并在鋪墊式問題的引領之下，獲得解題自信.想來，這也是所謂“春風化雨、潤物細聲”的高品質教學之追求吧.