一種基于正態(tài)分布的復(fù)雜網(wǎng)絡(luò)結(jié)構(gòu)劃分算法
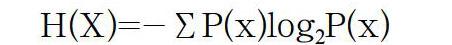
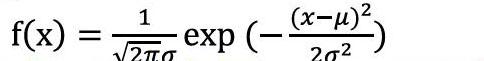
摘? 要:復(fù)雜網(wǎng)絡(luò)的節(jié)點(diǎn)聚集呈現(xiàn)符合社區(qū)結(jié)構(gòu)的動(dòng)態(tài)、無(wú)標(biāo)度和非對(duì)稱的特性,為了優(yōu)化復(fù)雜網(wǎng)絡(luò)的社區(qū)結(jié)構(gòu),研究當(dāng)前發(fā)現(xiàn)和優(yōu)化社區(qū)結(jié)構(gòu)的方法的不足,研究用約束正態(tài)分布來(lái)改進(jìn)社區(qū)結(jié)構(gòu)的節(jié)點(diǎn)聚集歸屬方法,借助信息熵,提出了基于正太分布的復(fù)雜網(wǎng)絡(luò)結(jié)構(gòu)劃分算法,通過(guò)算法得出聚集節(jié)點(diǎn)的正態(tài)分布概率,用正太分布概率作為信息熵的輸入,重新調(diào)整信息熵的變化,根據(jù)信息熵變化的幅度,確定節(jié)點(diǎn)的劃分歸屬。本算法在確定網(wǎng)絡(luò)社區(qū)結(jié)構(gòu)劃分的同時(shí),也能夠確定社區(qū)內(nèi)節(jié)點(diǎn)的模糊關(guān)系。
關(guān)鍵詞:正太分布;復(fù)雜網(wǎng)絡(luò);社區(qū)結(jié)構(gòu);結(jié)構(gòu)精簡(jiǎn);優(yōu)化算法
中圖分類(lèi)號(hào):TP393? ? ?文獻(xiàn)標(biāo)識(shí)碼:A
Abstract:The node aggregation of complex networks presents the dynamic,fuzzy and asymmetrical characteristics of the community structure.In order to optimize the community structure of complex networks,the paper studies the current methods of discovering and optimizing community structures,and the node aggregation method to improve the community structure by constraining normal distribution.Based on information entropy,the paper proposes a complex network structure partitioning algorithm based on positive distribution.The normal distribution probability of the aggregation node is obtained by the algorithm.The positive distribution probability is used as the input of information entropy to re-adjust the information entropy.According to the magnitude of the information entropy change,the division of the node is determined.The algorithm can determine the fuzzy relationship of nodes in the community while determining the division of the network community structure.
Keywords:normal distribution;complex network;community structure;structure simplification;optimization algorithm
1? ?引言(Introduction)
復(fù)雜網(wǎng)絡(luò)中社區(qū)發(fā)現(xiàn)的研究是當(dāng)前國(guó)內(nèi)外研究的熱點(diǎn)之一,社區(qū)結(jié)構(gòu)作為復(fù)雜網(wǎng)絡(luò)重要的特性,對(duì)認(rèn)識(shí)節(jié)點(diǎn)內(nèi)部關(guān)聯(lián)、信息傳播、興趣點(diǎn)推薦等具有重要的研究?jī)r(jià)值。復(fù)雜網(wǎng)絡(luò)社區(qū)檢測(cè)是指從復(fù)雜網(wǎng)絡(luò)中挖掘出有實(shí)際意義的模塊或?qū)哟谓Y(jié)構(gòu)的過(guò)程,能夠提取出網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)特征,有助于理解和分析網(wǎng)絡(luò)的拓?fù)涮匦浴⒐δ芴匦约皠?dòng)力學(xué)特性,挖掘出復(fù)雜網(wǎng)絡(luò)中蘊(yùn)含的屬性關(guān)聯(lián)性等深層次信息并對(duì)網(wǎng)絡(luò)行為進(jìn)行預(yù)測(cè)[1]。
目前研究人員對(duì)復(fù)雜網(wǎng)絡(luò)社區(qū)結(jié)構(gòu)的劃分和檢測(cè)進(jìn)行了大量的研究:文獻(xiàn)[2]提出一種基于k-派系滲透的動(dòng)態(tài)網(wǎng)絡(luò)社區(qū)檢測(cè)算法,該算法需要以較長(zhǎng)的檢測(cè)時(shí)間作為代價(jià)實(shí)現(xiàn)重疊社區(qū)的檢測(cè);文獻(xiàn)[3]提出一種探尋復(fù)雜網(wǎng)絡(luò)最短路徑的近似算法;文獻(xiàn)[4]提出一個(gè)融合貝葉斯概率的社區(qū)結(jié)構(gòu)發(fā)現(xiàn)方法研究;文獻(xiàn)[5]提出動(dòng)態(tài)社區(qū)的點(diǎn)增量發(fā)現(xiàn)算法;文獻(xiàn)[6]提出基于單目標(biāo)PSO的社區(qū)檢測(cè)算法;文獻(xiàn)[7]提出節(jié)點(diǎn)相似度感知的DTN交疊社區(qū)結(jié)構(gòu)檢測(cè)機(jī)制;文獻(xiàn)[8]提出局部?jī)?yōu)先的社會(huì)網(wǎng)絡(luò)社區(qū)結(jié)構(gòu)檢測(cè)算法;文獻(xiàn)[9]提出社交網(wǎng)絡(luò)中基于近似因子的自適應(yīng)社區(qū)檢測(cè)算法。文獻(xiàn)[10]提出一種基于常量因子近似的動(dòng)態(tài)社區(qū)檢測(cè)算法,但該算法需要確定明確量化的懲罰成本,而復(fù)雜動(dòng)態(tài)網(wǎng)絡(luò)多數(shù)情況無(wú)法預(yù)知該懲罰成本,因此,該算法對(duì)現(xiàn)實(shí)復(fù)雜網(wǎng)絡(luò)不具有可行性。
針對(duì)上述問(wèn)題,本文提出一種基于正太分布的復(fù)雜網(wǎng)絡(luò)結(jié)構(gòu)劃分算法(A Complex Network Structural division Algorithm Based on Normal Distribution,CSAN)并利用具有社區(qū)結(jié)構(gòu)的已知網(wǎng)絡(luò)現(xiàn)實(shí)數(shù)據(jù)檢驗(yàn)算法的有效性。本文算法的特點(diǎn)是:①算法從中心μ開(kāi)始擴(kuò)展,通過(guò)距離密度閾值的探測(cè),探查社區(qū)結(jié)構(gòu),實(shí)現(xiàn)社區(qū)結(jié)構(gòu)的擴(kuò)展;②算法形成有效社區(qū)結(jié)構(gòu)劃分的同時(shí),也能夠把社區(qū)結(jié)構(gòu)中遠(yuǎn)離社區(qū)中心μ的節(jié)點(diǎn)重新歸類(lèi),減輕社區(qū)結(jié)構(gòu)的節(jié)點(diǎn)冗余,提高社區(qū)結(jié)構(gòu)的工作效率。
2? ?問(wèn)題建模(Problem modeling)
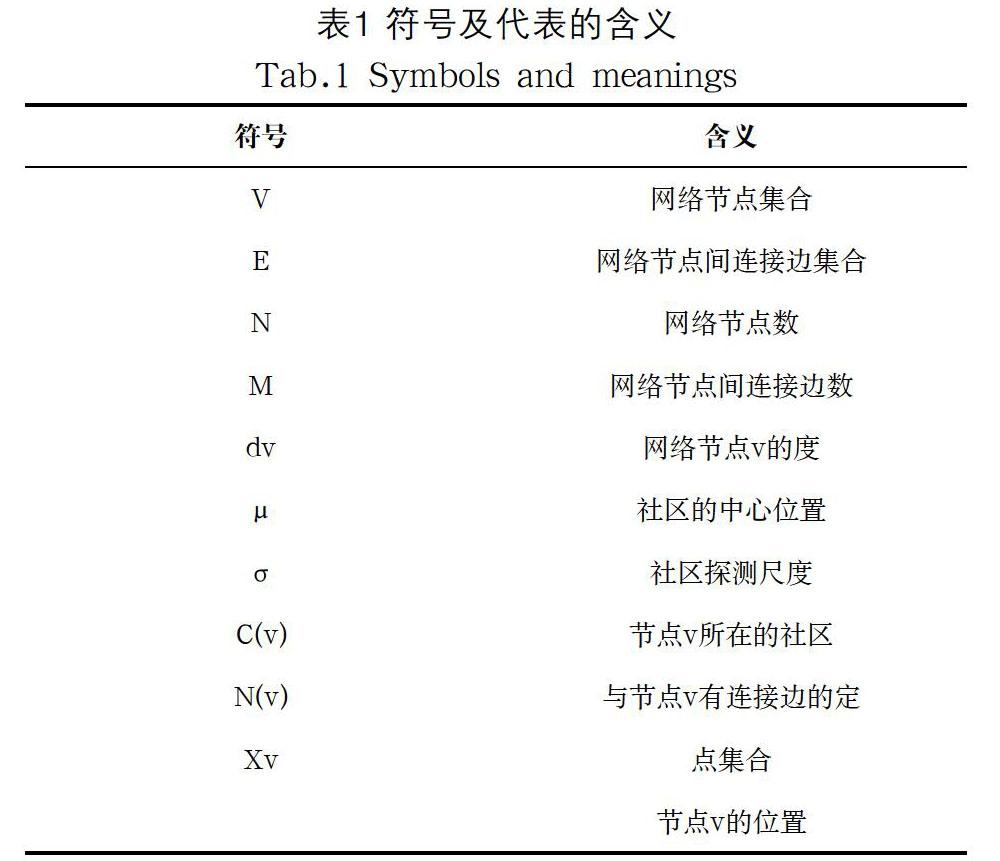
復(fù)雜網(wǎng)絡(luò)可以用一個(gè)無(wú)向圖G=(V,E)表示,其中,節(jié)點(diǎn)數(shù)量為N=|V|,復(fù)雜網(wǎng)絡(luò)中節(jié)點(diǎn)間連接邊的數(shù)量為M=|E|。節(jié)點(diǎn)間連接邊的鄰接矩陣A表示為A=(Aij),如果節(jié)點(diǎn)i和j之間有一條邊連接,則Aij=1,否則Aij=0。用C=(C1,C2,…,Ck)表示復(fù)雜網(wǎng)絡(luò)中的社區(qū),CSi(i=1,2,…,k)表示i社區(qū)的社區(qū)結(jié)構(gòu)。表1列出了本文涉及的符號(hào)和各自代表的含義。
2.1? ?信息熵
信息熵[11]是信息論中用于度量信息量的一個(gè)概念,它是有明確定義的科學(xué)名詞,不隨信息的具體表達(dá)形式的變化而改變,是抽象的概念。香農(nóng)在1948年第一次提出“信息熵(Information Entropy)”的概念,在香農(nóng)的概念中,信息是消除或減少不確定性的東西。獲得信息,意味著不確定性的減少。不確定性的減少導(dǎo)致“熵”減小,即信息熵越小,表示事件的不確定性越小,則包含的信息量越小;反之則大。信息熵的計(jì)算公式如下:
其中,x∈X,X表示一個(gè)離散的隨機(jī)變量,P(x)表示一個(gè)概率密度函數(shù),-log2P(x)表示在狀態(tài)x下所含信息量或者不確定性數(shù)量。
2.2? ?正態(tài)分布
正態(tài)分布是數(shù)理統(tǒng)計(jì)中非常重要的一種概率分布,在解決與中心點(diǎn)距離有關(guān)的概率分布具有很廣泛的應(yīng)用。正態(tài)分布的概率密度函數(shù)為:
2.3? ?信息熵值探測(cè)模型
社區(qū)結(jié)構(gòu)的節(jié)點(diǎn)聚集具有距離靠近聚集的大概率[12],為此我們通過(guò)探測(cè)社區(qū)C中節(jié)點(diǎn)v在正太分布概率密度下的信息熵H(Xv)的值來(lái)確定初始社區(qū)的第一個(gè)節(jié)點(diǎn),以此節(jié)點(diǎn)為基準(zhǔn),根據(jù)探測(cè)的尺度發(fā)現(xiàn)新成員,最終形成一個(gè)網(wǎng)絡(luò)社區(qū)。
3? 基于正太分布的復(fù)雜網(wǎng)絡(luò)結(jié)構(gòu)劃分算法(Complex network structure division algorithm based on normal distribution)
首先,要確定復(fù)雜網(wǎng)絡(luò)社區(qū)的探測(cè)“中心點(diǎn)”,依據(jù)中心點(diǎn)計(jì)算概率密度覆蓋區(qū)域內(nèi)節(jié)點(diǎn)的信息上值,通過(guò)信息熵值與閾值之間的對(duì)比關(guān)系來(lái)進(jìn)一步確定進(jìn)入社區(qū)的節(jié)點(diǎn),從而構(gòu)建探測(cè)和優(yōu)化社區(qū)結(jié)構(gòu)。
算法1 探測(cè)復(fù)雜網(wǎng)絡(luò)的社區(qū)“中心點(diǎn)”
在算法2的第6步會(huì)產(chǎn)生現(xiàn)有復(fù)雜網(wǎng)絡(luò)的一些孤立節(jié)點(diǎn),這些節(jié)點(diǎn)的集合R=∑LCCk(k=0,1,2,…)。集合R的規(guī)模決定了復(fù)雜網(wǎng)絡(luò)在基于正太分布的社區(qū)發(fā)現(xiàn)過(guò)程中,剔除冗余節(jié)點(diǎn)的比例R/N,對(duì)于規(guī)模龐大的復(fù)雜網(wǎng)絡(luò)來(lái)說(shuō),具有一定的優(yōu)化作用。
4? ?驗(yàn)證(Experimental verification)
通過(guò)實(shí)驗(yàn)的方式檢驗(yàn)上述算法在復(fù)雜網(wǎng)絡(luò)社區(qū)結(jié)構(gòu)發(fā)現(xiàn)和優(yōu)化中的可行行,算法可以發(fā)現(xiàn)不能劃分到社區(qū)的節(jié)點(diǎn),從而展示算法的有效性。
實(shí)驗(yàn)數(shù)據(jù)來(lái)源于實(shí)驗(yàn)機(jī)房隨機(jī)選定的8臺(tái)計(jì)算機(jī),每臺(tái)計(jì)算機(jī)都能夠通過(guò)級(jí)聯(lián)的交換機(jī)互聯(lián),其中編號(hào)0—3的計(jì)算機(jī)連接在1號(hào)交換機(jī),4—7號(hào)計(jì)算機(jī)連接在2號(hào)交換機(jī)。利用算法2計(jì)算節(jié)點(diǎn)之間的熵值關(guān)系矩陣如表2所示。矩陣的值表示有序節(jié)點(diǎn)之間的連接概率,矩陣值越大,反映出節(jié)點(diǎn)之間的同社區(qū)可能性越大,根據(jù)設(shè)定的閾值ε=0.5,通過(guò)算法的執(zhí)行,得到節(jié)點(diǎn)逐步優(yōu)化分割的社區(qū)結(jié)構(gòu)。
通過(guò)閾值的調(diào)整,可以進(jìn)一步改進(jìn)社區(qū)結(jié)構(gòu)的節(jié)點(diǎn)聚集關(guān)系,從而可以實(shí)現(xiàn)復(fù)雜網(wǎng)絡(luò)的優(yōu)化升級(jí)。
算法執(zhí)行過(guò)程中,對(duì)應(yīng)的節(jié)點(diǎn)變化走勢(shì)如圖1所示。
從算法執(zhí)行的過(guò)程,能夠看出社區(qū)結(jié)構(gòu)的形成是符合實(shí)際的有價(jià)值的結(jié)構(gòu),對(duì)于信息熵值低于閾值的節(jié)點(diǎn)將從不隸屬于任何一個(gè)社區(qū)結(jié)構(gòu),這些點(diǎn)從復(fù)雜網(wǎng)絡(luò)中獨(dú)立劃分,單獨(dú)處理。本算法的時(shí)間復(fù)雜度為O(N2),隨著網(wǎng)絡(luò)規(guī)模的急劇增長(zhǎng),算法的計(jì)算時(shí)間曲線斜率線性增長(zhǎng),耗費(fèi)大量的系統(tǒng)時(shí)間。算法的計(jì)算時(shí)間同網(wǎng)絡(luò)規(guī)模之間的關(guān)系如圖2所示。
5? ?結(jié)論(Conclusion)
復(fù)雜網(wǎng)絡(luò)的節(jié)點(diǎn)聚集呈現(xiàn)符合社區(qū)結(jié)構(gòu)的動(dòng)態(tài)、無(wú)標(biāo)度和非對(duì)稱的特性,為了優(yōu)化復(fù)雜網(wǎng)絡(luò)的社區(qū)結(jié)構(gòu),本文提出的提出一種基于正態(tài)分布的復(fù)雜網(wǎng)絡(luò)結(jié)構(gòu)優(yōu)化算法(CSAN),本算法既能發(fā)現(xiàn)并重構(gòu)社區(qū)結(jié)構(gòu),也能發(fā)現(xiàn)社區(qū)內(nèi)節(jié)點(diǎn)之間的動(dòng)態(tài)模糊指向關(guān)系,采用了信息熵的變化來(lái)發(fā)掘社區(qū)節(jié)點(diǎn),同時(shí),能夠發(fā)掘網(wǎng)絡(luò)中的信息相對(duì)孤立的冗余節(jié)點(diǎn),這些節(jié)點(diǎn)不劃歸任何一個(gè)社區(qū),從而優(yōu)化了社區(qū)結(jié)構(gòu),精簡(jiǎn)了社區(qū)規(guī)模,這是本研究的創(chuàng)新之處。現(xiàn)實(shí)中,復(fù)雜網(wǎng)絡(luò)節(jié)點(diǎn)之間的關(guān)系復(fù)雜,存在多種關(guān)系形態(tài),如關(guān)聯(lián)關(guān)系,因果關(guān)系,相反關(guān)系等,深入研究這種關(guān)系對(duì)于復(fù)雜網(wǎng)絡(luò)的優(yōu)化具有十分重要的意義。本研究只用簡(jiǎn)單的局域網(wǎng)進(jìn)行了檢驗(yàn),檢驗(yàn)算法的數(shù)據(jù)有限,在實(shí)際復(fù)雜網(wǎng)絡(luò)環(huán)境下本算法的具體性能研究還需要做進(jìn)一步的檢驗(yàn)工作。對(duì)根據(jù)信息熵的變化和社區(qū)結(jié)構(gòu)具有位置相對(duì)靠近聚集的特點(diǎn),采用正態(tài)分布概率密度作為信息熵值估計(jì),從而判斷節(jié)點(diǎn)是否屬于一個(gè)社區(qū),熵閾值確定很重要,如何確定更好的閾值,使得發(fā)現(xiàn)的社區(qū)結(jié)構(gòu)有更好的可用性,這也是目前所有社區(qū)發(fā)現(xiàn)方法面臨的問(wèn)題,也是下一步的重點(diǎn)研究方向。本研究所涉算法的復(fù)雜度偏高,如何降低社區(qū)結(jié)構(gòu)發(fā)現(xiàn)和優(yōu)化的算法時(shí)間復(fù)雜度也是下一步研究的方向。
參考文獻(xiàn)(References)
[1] Qiao Shao-Jie,Guo Jun,Han Nan,et al.Parallel Algorithm for Discovering Communities in Large-Scale Complex Networks[J].Chinese Journal of Computers,2017,3(40):687-700.
[2] Roy S D,LotanG,ZengWenjun.The Attention Automaton:Sensing Collective User Interests in Social Network Communities[J].IEEETransactionsonNetworkScienceand Engineering,2015,2(1):40-52.
[3] TANGJin-Tao,WANGTing,WANGJi.Shortest Path Approximate Algorithm for Complex Network Analysis[J].Journal of Software,2011,22(10):2279-2290.
[4] 王剛.一個(gè)融合貝葉斯概率的社區(qū)結(jié)構(gòu)發(fā)現(xiàn)方法研究[J].計(jì)算機(jī)技術(shù)與發(fā)展,2018(12):1-5.
[5] 顧炎,熊超.動(dòng)態(tài)社區(qū)的點(diǎn)增量發(fā)現(xiàn)算法[J].計(jì)算機(jī)技術(shù)與發(fā)展,2017,27(6):81-85.
[6] 楊令興,張喜斌.基于單目標(biāo)PSO的社區(qū)檢測(cè)算法[J].計(jì)算機(jī)科學(xué),2015,42(6A):57-60.
[7] 王崢,王于波,朱承治.節(jié)點(diǎn)相似度感知的DTN交疊社區(qū)結(jié)構(gòu)檢測(cè)機(jī)制[J].微電子學(xué)與計(jì)算機(jī),2017,34(12):74-78.
[8] 李春英,湯志康,湯庸,等.局部?jī)?yōu)先的社會(huì)網(wǎng)絡(luò)社區(qū)結(jié)構(gòu)檢測(cè)算法[J].計(jì)算機(jī)科學(xué)與探索,2018,12(08):1263-1274.
[9] 闕建華.社交網(wǎng)絡(luò)中基于近似因子的自適應(yīng)社區(qū)檢測(cè)算法[J].計(jì)算機(jī)工程,2016(05):134-138.
[10] TantipathananandhC,Berger-Wolf T.Constant-factor Approximation Algorithms for Identifying Dynamic Communities[C].Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Paris,F(xiàn)rance,June 28-July 1,2009:827-836.
[11] Peng CG,Ding HF,Zhu YJ,et al.Informationentropy models and privacy metrics methods for privacy protection[J].Journal of Software,2016,27(8):1891-1903.
[12] 李兆南,楊博,劉大有.復(fù)雜網(wǎng)絡(luò)社區(qū)挖掘的距離相似度算法[J].計(jì)算機(jī)科學(xué)與探索,2011,5(4):336-344.
作者簡(jiǎn)介:
段忠祥(1978-),男,碩士,高級(jí)實(shí)驗(yàn)師.研究領(lǐng)域:軟件設(shè)計(jì),計(jì)算機(jī)應(yīng)用技術(shù),高職教育.
- 軟件工程的其它文章
- 工程應(yīng)用導(dǎo)向的面向?qū)ο笙盗姓n程體系重構(gòu)
- 高職計(jì)算機(jī)專(zhuān)業(yè)創(chuàng)客學(xué)校項(xiàng)目資源池(PR-POOL)模式的研究與實(shí)踐
- 跨境電商網(wǎng)站系統(tǒng)的分析與設(shè)計(jì)
- 水聲裝配試驗(yàn)生產(chǎn)線異構(gòu)數(shù)據(jù)采集系統(tǒng)設(shè)計(jì)
- 基于Redis的氣象數(shù)據(jù)分發(fā)管理系統(tǒng)的設(shè)計(jì)與實(shí)現(xiàn)
- 基于JavaScript的葉綠素?zé)晒庑盘?hào)特征點(diǎn)自動(dòng)定位軟件設(shè)計(jì)

