基于貝葉斯網絡的塔里木河流域豐枯遭遇分析*

2019-06-04 07:47:26陳長清1查顯能

水資源開發與管理 2019年5期

陳長清1 查顯能嚴冬

(1.塔里木河流域干流管理局，新疆庫爾勒 841000；2.華中科技大學水電與數字化工程學院，湖北武漢 430074)

塔里木河流域位于新疆南部，在天山山脈和昆侖山脈之間，是中國第一大內陸河，主要由阿克蘇河、和田河和葉爾羌河匯合而成。由于三源流區的水文特性受氣候、下墊面及人類活動的影響，使得三源流年徑流量的豐枯變化存在差異性和不確定性，這種不確定性導致了匯入塔里木河干流的年徑流量不同豐枯遭遇，直接影響著塔里木河中下游的調水用水的風險。因此對匯入塔里木河干流年徑流量的豐枯遭遇的預測需求變得十分迫切。

目前國內外對于貝葉斯網絡用于風險分析也有許多研究和嘗試，周建方等[1]將多個事件樹凝練綜合成一個貝葉斯網絡，分析了沙河集水庫大壩的安全風險；林鵬智等[2]建立了不同因素單獨、綜合作用下的單庫、梯級系統漫壩貝葉斯網絡風險分析模型，分析了漫頂風險的主導因素；康玲等[3]對南水北調中線水源區和受水區降雨豐枯遭遇建立貝葉斯網絡，通過情景仿真和后驗推理功能，模擬了不同豐枯組合對調水的影響；Daniel[4]利用并驗證了非參數蒙特卡洛貝葉斯理論在洪水頻率分析中的獨特優勢；H.VAN de Vyver[5]利用貝葉斯網絡對降雨極值強度-持續時間頻率相關關系進行了分析，并與傳統方法進行對比，驗證了貝葉斯方法的優越性。本文擬根據貝葉斯網絡理論及節點條件概率，建立塔里木河流域年徑流量風險遭遇貝葉斯網絡結構，分析塔里木河流域三源流的不同年徑流組合對干流年徑流豐枯遭遇的影響。

1 貝葉斯網絡

貝葉斯網絡[6](Bayesian Network，BN)，又稱信念網絡，是由 Judea Pearl 于 1985年首先提出的一種模擬人類推理過程中因果關系的不確定性處理模型。貝葉斯網絡是概率、統計與圖論組合由有向無環圖模型(DAG)和條件概率表(CPTs)組成的概率推理與診斷工具，它將風險管理中的風險因素用網絡節點的先驗概率表示，用有向邊代表節點間的相互關系，由條件概率表達。

若令G=(I,E)表示一個有向無環圖(DAG)，其中I代表圖形中所有節點的集合，而E代表有向連接線的集合，且令X=xi,i∈I為其有向無環圖中的某一節點i所代表的隨機變量，若節點X的聯合概率可以表示成下式：

(1)

則稱X為相對于一有向無環圖G的貝葉斯網絡，其中，xpa(i)表示節點i之“因”，或稱xpa(i)是i的“父節點”(parents)。根據全概率公式，對于任意的隨機變量，其聯合概率可由局部條件概率分布相乘而得出下式[7]：

p(x1,…,xk)=p(xk|x1,…xk-1)…p(x2|x1)p(x1)

(2)

貝葉斯網絡可以用于分析和表達不確定事件和概率性事件。通過建立貝葉斯網絡，用節點和連接這些結點的有向邊將實際問題抽象化，節點變量可以表達不確定事件間的相互條件概率，有向邊可以表示不確定事件間的“子、父節點”關系，由父節點指向子節點。把事件的先驗知識通過概率和節點之間的聯合概率分布來表示。通過調整節點的概率，實現對后驗知識的學習和推理。

2 資料分析

2.1 設計值確定

本文收集了塔里木河流域阿克蘇河、葉爾羌河、和田河及塔里木河干流上協合拉、沙里桂蘭克、烏魯瓦提、同古孜洛克、卡群、阿拉爾6個水文站1957—2016年的實測徑流資料。其中，阿克蘇河天然徑流系列資料為庫瑪拉克河協合拉水文站監測數據和托什干河沙里桂蘭克水文站監測數據之和；和田河天然徑流采用喀拉喀什河烏魯瓦提水文站監測數據和玉龍喀什河同古孜洛克水文站監測數據之和；葉爾羌河天然徑流采用卡群水文站監測數據；塔里木河干流天然徑流采用阿拉爾水文站監測數據。

以皮爾遜三型頻率分布曲線得出逐年各頻率的設計值。其中豐平枯年等級劃分標準見表1。

表1 豐、平、枯等級劃分標準

根據表1的豐、平、枯等級劃分標準可以確定所求的設計值為X37.5%和X62.5%,這里通過繪制皮爾遜三型曲線得到所需頻率的設計值，進而劃分豐、平、枯年份，見表2。

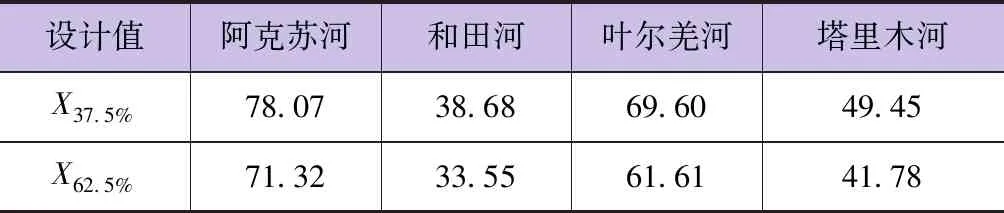
表2 各河段年徑流量特定頻率設計值單位：億m3

2.2 豐枯遭遇組合

利用統計方法得到三源流年徑流量 27 種豐枯遭遇組合狀態，見表3。

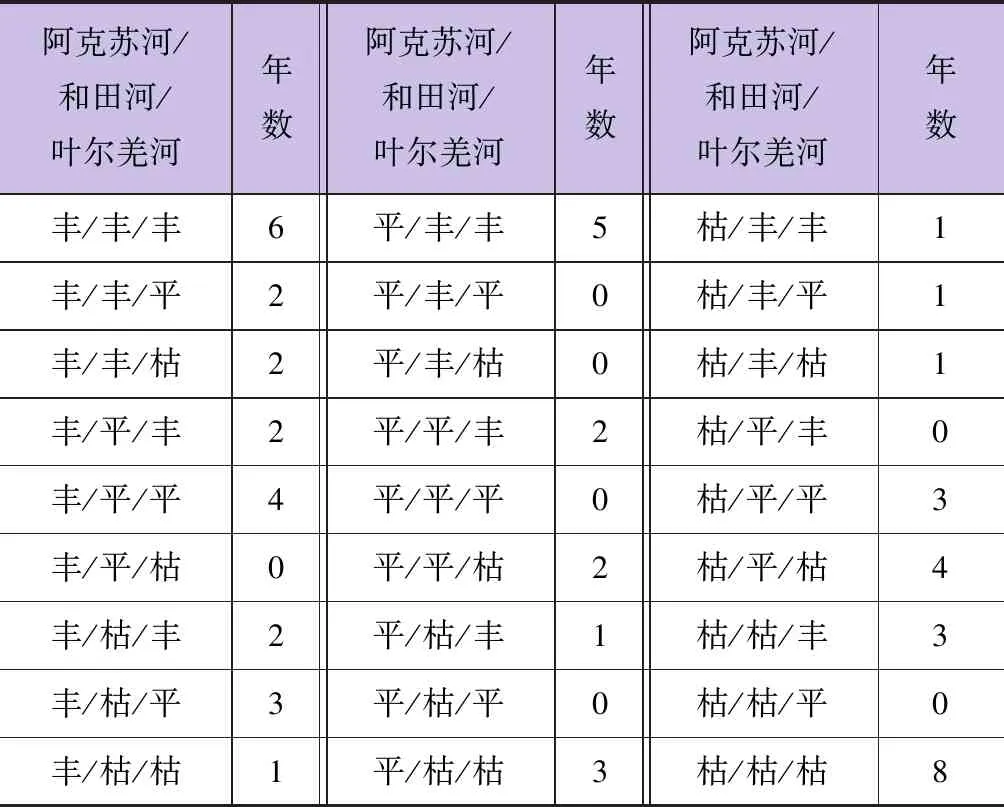
表3 源流豐枯27種組合統計結果

3 貝葉斯網絡豐枯遭遇風險管理模型

貝葉斯網絡結構模型的建立主要有以下3個步驟：?確定網絡結構；?獲得網絡參數；?利用后驗知識仿真模擬。

3.1 確定網絡結構

貝葉斯網絡結構的確定方法有兩種[8]：?通過大量實測數據的結構學習獲得；?由專家知識獲得，即根據專家對變量之間的因果依賴關系勾畫出網絡結構，這種方法對數據的多少要求不高，較為簡便。本文采用第二種方法，通過分析各源流區豐枯組合對干流徑流量組合的影響，建立豐枯遭遇風險管理模型，其模型結構見圖1。

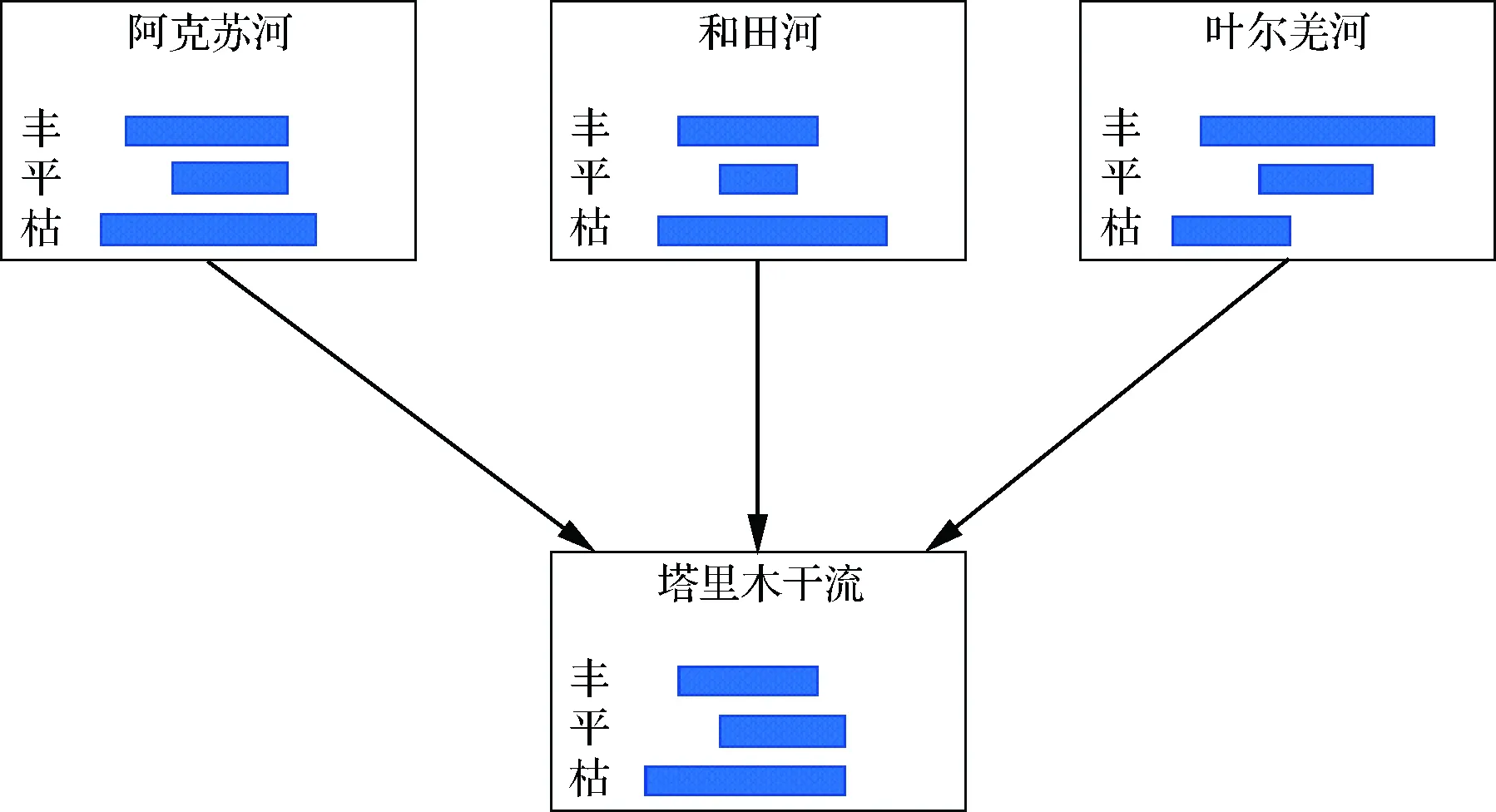
圖1 貝葉斯網絡結構

圖1中是以阿克蘇河、和田河和葉爾羌河的年徑流量為父節點，以塔里木河的年徑流量為子節點，考慮在三源流不同豐平枯組合下，塔里木河的年徑流量豐枯遭遇。

3.2 網絡參數獲取

網絡參數即根節點的先驗概率和非根節點的條件概率。在建立了網絡結構的基礎上，結合樣本統計數據，計算根節點的先驗概率和中間節點的條件概率，輸入并完成貝葉斯網絡結構。

模型中父節點的先驗概率[9]可以通過56年各河段年徑流量豐平枯的分布計算獲得，子節點的條件概率根據表3中各源流豐平枯27種組合情況下塔里木河的豐平枯概率分布計算獲得：

(3)

式中：Ai為27種豐平枯組合中的第i種情況；Bj為塔里木河干流豐平枯情況，j取豐、平和枯3種情況。

將計算出的各種豐枯遭遇概率輸入網絡結構中得到貝葉斯網絡初始模型，見圖2。

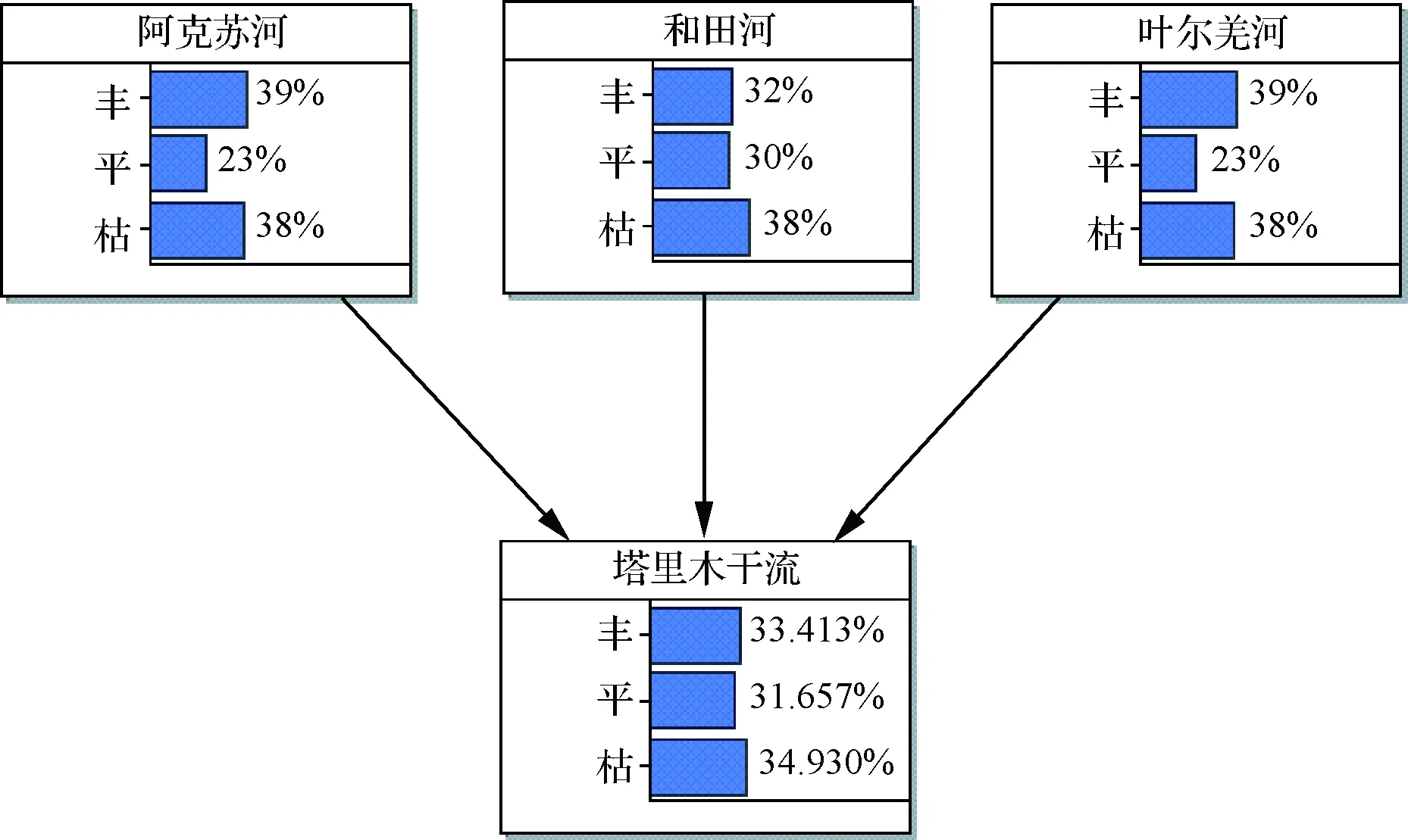
圖2 豐枯遭遇貝葉斯網絡

圖2中可以看出：阿克蘇河與葉爾羌河的年徑流量的豐平枯遭遇基本相似，豐水概率為39%，平水23%，枯水38%，豐水概率與枯水概率相差不大，平水概率較小。和田河的豐水概率為32%，平水30%，枯水38%，其中枯水更易發生。相比三源流可見，在枯水發生概率上基本近似，但在豐水發生概率上阿克蘇河與葉爾羌河較高。由貝葉斯網絡計算出的塔里木河干流年徑流量的概率與實際先驗知識基本相同，豐枯平水年的分布概率也基本接近。

3.3 仿真模擬

貝葉斯網絡不僅可以通過實測數據計算塔里木河干流年徑流量的豐枯遭遇概率，即先驗概率，還可以通過預測某一節點或多個節點的豐枯遭遇情況，以此為后驗信息輸入到貝葉斯網絡中，通過網絡模型的方向推理功能，推測出此節點的變動情況對其他節點的概率影響，為決策者制定應急方案提供數據支撐。考慮塔里木河干流對下游輸水的保證，故干流的年徑流量的枯水年應值得關注，本文以阿克蘇河為枯水，阿克蘇河、葉爾羌河均為枯水以及三源流均為枯水這3種情境作為后驗信息輸入到貝葉斯網絡結構中進行仿真研究。

a.情境模擬一：將阿克蘇河年徑流為枯水情況輸入貝葉斯網絡結構中得到仿真計算結果，見圖3。

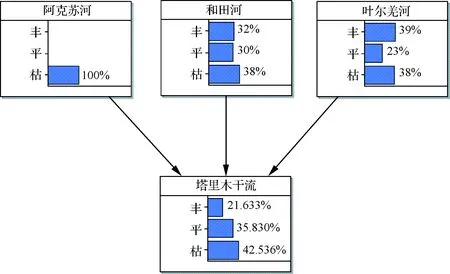
圖3 阿克蘇河為枯水貝葉斯網絡

對比圖2分析可知：當輸入阿克蘇河年徑流為枯水這一后驗信息后，塔里木河干流的豐平枯遭遇發生較大變化，其中豐水概率由33.413%降為21.633%，平水概率略微上升，枯水概率由34.930%上升為42.536%。由表2可知阿克蘇河的徑流是三源流中流量最多的，故阿克蘇河為枯水時，對匯聚塔里木河干流流量影響較大，表現為下游徑流量明顯減小，枯水更易于發生，豐水難于發生。同時，研究表明：在1994—2003年阿克蘇河為特豐水時，和田河和葉爾羌河也為偏豐水時段[10]，塔里木河干流流量更易為豐水。

b.情境模擬二：貝葉斯網絡對于后驗信息輸入的節點個數沒有限制，以兩節點輸入為例，將阿克蘇河和葉爾羌河年徑流為枯水情況輸入貝葉斯網絡結構中得到仿真計算結果，見圖4。

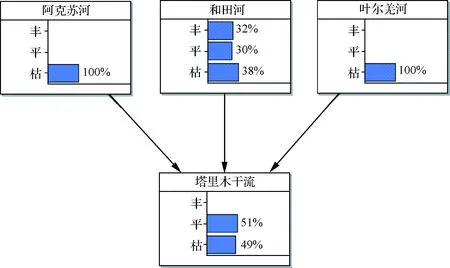
圖4 阿克蘇河、葉爾羌河為枯水的貝葉斯網絡

相比于初始網絡模型圖2可知:當阿克蘇河、葉爾羌河均為枯水時，塔里木河干流的豐枯遭遇發生大幅變化。豐水概率由33.413%下降為0，平水概率由31.657%上升為51%，枯水概率由34.930%上升為49%，并在圖4的基礎上塔里木河干流的枯水概率更為上升，年徑流量減幅明顯，可知，阿克蘇河和葉爾羌河徑流對塔里木河干流徑流的豐枯遭遇影響較大，且占主導作用。對于圖4的情況，相關部門應采取針對性的應急預案措施。

c.情境模擬三：以三源流均為枯水的后驗信息輸入貝葉斯網絡，得到圖5。

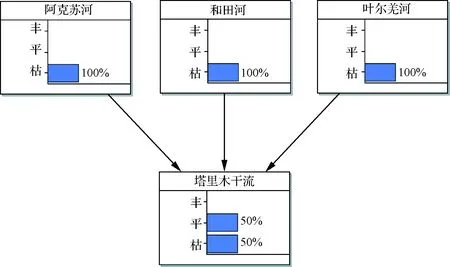
圖5 三源流均為枯水的貝葉斯網絡

當三源流均為枯水時，相比圖4，塔里木河干流平水概率微降，枯水概率微升，這是由于和田河的流量在三源流中為最少，故匯聚在塔里木河干流的權重較小，引起塔里木河干流豐枯遭遇的變化幅度較其他兩河源要小。但圖5中整體表現的結果為三源流均枯的情況下，導致塔里木河干流的枯水概率較高，為50%，平水概率為50%，無豐水可能性。