有機玻璃觀察窗的蠕變特性及數值模擬

郭大猷，黃小平，王 芳

(1.上海交通大學 高新船舶與深海開發裝備協同創新中心，上海 200240；2.上海海洋大學 上海深淵科學工程技術研究中心，上海 201306)

載人深潛器的研發對于我國開發利用深海資源有著重要的意義，其中觀察窗作為重要的開口結構，對于保障深潛器和作業人員的安全至關重要.觀察窗的材料一般采用有機玻璃(PMMA)，其力學特性不同于通常的線性或者非線性材料，表現為對環境和加載方式敏感.

若嚴格按照ASME規范的設計要求，全海深潛水器載人艙的觀察窗厚度可能會超過設計限度，嚴重地限制了載人深潛器的發展.現階段，觀察窗的設計需要大量的數值模擬和實驗驗證.基于有限元法(FEM)的模擬由于能夠處理非線性問題(材料非線性、大變形、接觸等)而得到廣泛應用.

劉道啟等[1]指出，觀察窗與窗座之間的相對位移主要由兩部分構成：① 觀察窗與窗座在海水壓力作用下發生的擠壓變形；② 觀察窗玻璃隨時間的蠕變變形.由常溫下PMMA蠕變的回歸公式推導出反映蠕變變形的本構模型，采用有限元軟件得到的觀察窗隨時間蠕變的計算結果，與實驗分析結果接近.田常錄等[2]針對潛水器觀察窗的蠕變變形理論展開進一步的探索，獲得了觀察窗受力變形以及蠕變變形的計算公式,計算結果與實驗結果較為吻合.可見，針對保載階段蠕變的有限元模擬研究具有一定的準確性.

然而，隨著潛深的增加，下潛過程中觀察窗將受到更長時間、更高壓力的靜水載荷，這一階段的蠕變影響將變得十分重要.因此，為了更貼切地模擬觀察窗的作業流程，亟需一種能分析加壓-保載全過程的有限元方法.

首先必須獲得PMMA的材料模型，目前國內外的研究大多采用黏彈性本構關系模型.謝中秋等[3]在恒應變率加載單軸壓縮實驗中使用了含應變率效應的ZWT(朱王唐)黏彈性本構模型，并基于實驗數據獲取了PMMA材料的本構模型參數.Hu等[4]研究了溫度和應變率對PMMA力學性能的影響，提出了考慮溫度、應變率耦合影響的本構模型，研究結果與實驗結果吻合良好.Wang和Uzair等[5-6]對ZWT模型進行改進，在考慮溫度影響的情況下對PMMA的碰撞過程進行了建模分析.

考慮到觀察窗的工作環境相當于一個準靜態加載過程，本文借鑒文獻 [7] 的研究思路，采用廣義Maxwell模型表征PMMA的黏彈性材料特性，得出Prony級數形式的松弛彈性模量，進而結合有限元軟件Abaqus，采用質量縮放技術和等效時長方法加快了顯式動力計算過程，計算并校驗了觀察窗的蠕變變形.此外，針對觀察窗模型局部應力集中問題，通過設置倒角有效降低了局部應力，同時使得網格的收斂性更好.

1 觀察窗蠕變的黏彈性特性

當物體受到恒定外力時，其應力與變形隨時間變化的現象稱為蠕變.在海水壓力作用下，觀察窗變形主要包括與窗座間的擠壓變形和蠕變變形.考慮蠕變特性時，PMMA的應力-應變并不是簡單的線性關系，故不能僅以線彈性特征來描述其本構關系.

學界對PMMA等聚合物的認識經歷了一個逐步變化的過程，在模擬研究聚合物變形行為的時候曾將聚合物建立為彈塑性材料模型、超彈性材料模型、黏塑性材料模型，而近幾年隨著對聚合物力學性能研究的逐步深入，發現黏彈性材料模型更符合聚合物的變形特點[7].

1.1 PMMA的黏彈性力學模型

黏彈性的最大的特性就是與應變率相關，有蠕變、應力松弛等現象，并對時間和溫度有很大的依賴性[7].目前對PMMA黏彈性特征的表述可歸結為兩類：① 時溫等效性；② 在不同應變率下的松弛或蠕變行為.所謂時溫等效性，即可以通過確定位移因子用較高溫度的松弛實驗曲線平移得到低溫下的松弛實驗曲線，而位移因子可以由經典的Williams-Landell-Ferry(WLF)方程計算[7].另一方面，應變率的影響則表現為：恒定的實驗溫度下，隨著應變率增大，PMMA的流動應力顯著增加，且可以采用ZWT黏彈性本構模型進行擬合[3].

為表征聚合物這種黏彈性材料的力學行為，可以將其看成是由表征黏性的元件(用黏壺表示)和表征彈性的元件(用彈簧表示)組合起來的復合模型.由黏性和彈性元件的不同組合排列方式即可得出模擬黏彈性材料特性的各種模型[7].

最常用的表征黏彈性的模型是Maxwell模型和Kelvin模型，但由于其參數較少，難以準確表達較為復雜的蠕變規律.

黏彈性力學模型中的彈性和黏性單元越多，越能精確地表征出材料的黏彈性特性.本文所采用的廣義Maxwell模型由n個Maxwell體和1個彈性元件并聯而成，如圖1所示.圖中：Ei和ηi(i=1,2,…,n)分別為各Maxwell體中彈性元件的彈性模量及黏壺的黏度；Ee為單獨彈性元件的彈性模量.

圖1 廣義Maxwell模型Fig.1 Generalized Maxwell model

考慮松弛問題，即從某初始時刻起對模型施加恒定應變，并且施加到并聯的每個Maxwell體上的應變大小相同.對于Maxwell體，將τi=ηi/Ei稱為松弛時間，基于Maxwell模型的應力松弛公式，各 Maxwell 元件的應力隨時間的變化應滿足

σi(t)=ε0Eie-t/τi

(1)

故廣義Maxwell模型的總應力為

(2)

從而瞬時的松弛模量

(3)

由以上的分析可知，廣義的Maxwell模型可以很好地表征聚合物的蠕變(或松弛)變形特征，且上述松弛模量的數學表達形式與Prony級數形式相近.Abaqus中的線性黏彈性分析正是基于松弛模量的Prony級數形式的積分式本構方程[7]的，據此可對觀察窗蠕變特性進行分析.

1.2 Abaqus中的線性黏彈性

有限元軟件Abaqus提供了線彈性、塑性、黏彈性等多種本構模型，結合靜態或顯式動態的求解方法，可模擬PMMA觀察窗在加壓-保載條件下的變形過程.本節重點介紹Abaqus中的黏彈性模型.

Abaqus提供了3種黏彈性的定義方式：① 基于頻域的黏彈性函數——適用于穩態、微幅振動分析；② 基于時域的黏彈性函數——適用于依賴時間的分析；③ 基于用戶指定的蠕變法則——適用于非線性黏彈性分析.本文采用基于時域的黏彈性本構關系來研究觀察窗的蠕變問題.

1.2.1適用條件 在定義連續彈性體材料的性質時，Abaqus的時域黏彈性模型假定切變和體積的變化行為在多軸應力狀態下是相互獨立的(不包括橡膠式泡沫(elastomeric foam)材料)，本構模型要能反映切變變形和體積變形的規律.黏彈性本構模型需要與線彈性，或類橡膠類物質的超彈性行為協同使用，并適用于大應變問題.

黏彈性主要在準靜態分析、隱式直接積分法的動態分析、顯式動態分析、穩態流動(transport)分析等分析類型中使用.黏彈性參數的輸入主要有兩種方法：① 按照歸一化的Prony級數格式輸入材料參數；② 直接輸入經標準化的松弛或蠕變實驗數據，由軟件自行計算生成本構模型.

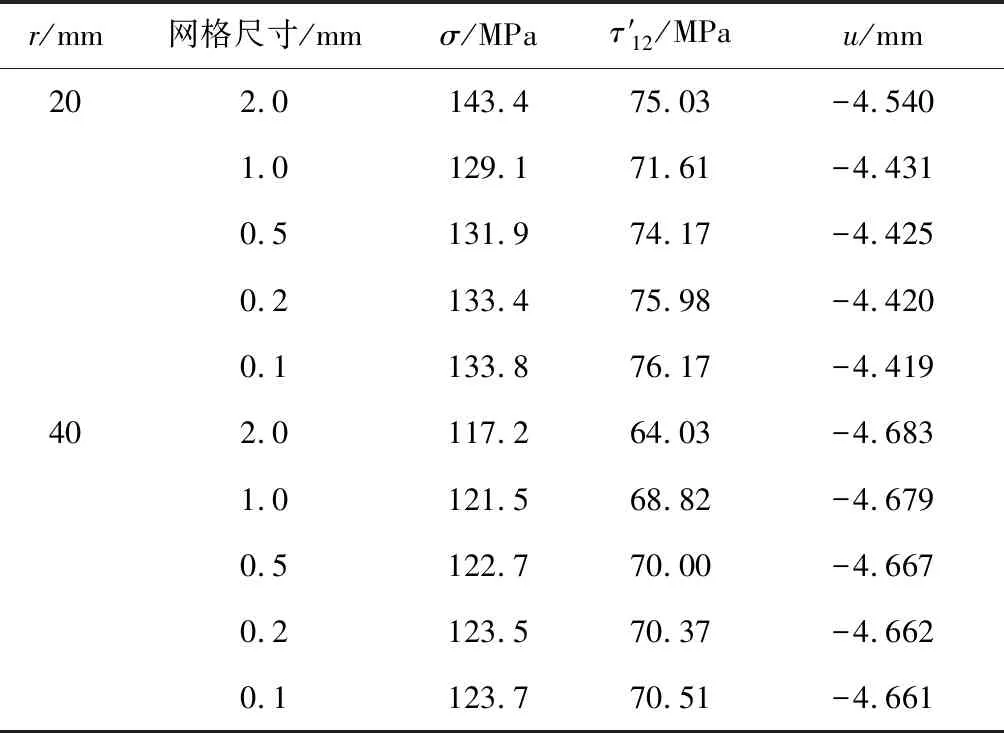
1.2.2數值計算 Abaqus通過對無量綱的松弛模量作Prony級數展開來定義黏彈性，如切變模量可表示為

(4)

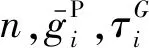
對體積模量作Prony級數展開，可獲得類似的數學形式：

(5)

且Abaqus假設

(6)

瞬時模量與初始模量、無量綱瞬時模量的關系為

GR(t)=G0gR(t)

(7)

KR(t)=K0kR(t)

(8)

在彈性范圍內，切變模量和體積模量與彈性模量和泊松比的關系為

(9)

為計算黏彈性響應，需要在Abaqus中輸入線彈性與線性黏彈性的相關參數.

2 觀察窗加壓-保載有限元模型

Wang等[8]開展的觀察窗加壓-保載實驗具有緩慢加載(不超過 4.5 MPa/min)、高壓下長時間穩壓保載(5 h)的特點，且實驗過程中溫度保持不變.因此，可對觀察窗PMMA材料的本構模型作出一定的簡化，即在恒溫條件下忽略WLF方程所考慮的時溫等效性，并將整個實驗過程視為準靜態加載，不考慮在動態加載下較高應變率對本構關系的影響.

本文參考文獻[8-9]的實驗，建立用于觀察窗加壓-保載分析的有限元模型，并驗證網格的收斂性.以觀察窗的下表面圓心為觀察點，對比線彈性、線性黏彈性兩種材料特性下的觀察窗變形情況，并與文獻中的實測數據進行對比.

2.1 有限元模型的建立

錐臺形觀察窗結構如圖2所示.圖中：觀察窗錐角為90°；下表面直徑為130 mm；厚度為153 mm.本文使用兩種模型：旋轉軸對稱平面模型(2D模型)和立體模型(3D模型).前者在對稱軸截面上取1/2模型，后者取1/4模型，分別如圖3和4所示，

圖2 深潛器的PMMA觀察窗設計尺寸 (mm)Fig.2 PMMA frustum design for deep-sea manned submersible (mm)

圖3 觀察窗2D模型Fig.3 2D model of observation window

圖4 觀察窗3D模型Fig.4 3D model of observation window

2.2 定義接觸和約束

接觸對之間的Kimematic接觸條件[10]認為：對于主接觸面Гs上的任意一點Ps，從接觸面Гc上在變形方向上的最近接觸點Pc可以通過它們之間的相對距離確定，其距離表達式為

(10)

式(10)為非線性方程，可以通過Newton-Raphson法求解.在t+Δt時刻，主從接觸面之間的距離可以表示為

t+ΔtS=[tPc-tPs]·t+ΔtN≥0

(11)

式中:t+ΔtN為t+Δt時刻的法向接觸體內的單位法向向量.式(11)可用線性表達式表示為

t+ΔtS=tS+

[Δtu(Pc)-Δtu(Ps)]·tN≥0

(12)

式中：Δu(P)為P點的位移矢量增量.

根據Koulomb準則，總摩擦力與黏連接觸及滑動接觸相關，即

(13)

本文以剛度大的窗座面作為主面，觀察窗作為從面，窗座與窗體相接觸并設置摩擦，取摩擦因數為 0.1.在模擬過程中，接觸方向總是主面的法線方向，從面上的節點不會穿越到主面，但主面上的節點可以穿越從面.對窗座底部施加固定約束，并在截面上建立對稱約束.

2.3 網格劃分及收斂性分析

基于線彈性本構關系開展網格收斂性分析，PMMA的彈性模量取 2.76 GPa，泊松比取 0.35(供貨商數據).模型外側施加115 MPa的靜水壓力作為載荷輸入.

對于3D模型，選用含有縮減積分和沙漏控制的8節點線性六面體單元(C3D8R)劃分網格，遵循接觸非線性分析中接觸主面網格尺寸大于從面的原則.靜力條件下試算得到的應力云圖如圖5所示.

圖5 靜力試算得到的應力云圖 (MPa)Fig.5 Stress contour plot of trial static analysis (MPa)

通過觀察應力分布情況，對窗體與窗座接觸的應力集中區域進行局部網格細化，以期得到更穩定的計算結果，網格劃分如圖6所示.

圖6 局部加密2 mm(過渡到4 mm)的3D模型Fig.6 Local grid refined 3D model (2—4 mm)

表1 無圓角3D模型在不同網格密度下的應力及位移
Tab.1 Stress and displacement of none-filleted 3D model with different mesh densities

網格尺寸/mmσ/MPaτ′12/MPau/mm6111.339.09-4.437489.5445.13-4.3472116.966.55-4.335

為了加快收斂分析的計算速度，轉而采用2D模型，使用旋轉軸對稱(Axisymmetric)單元劃分網格，并通過類似3D模型的方法對網格局部加密，如圖7所示.對于無圓角過渡的模型，在網格加密的過程中，觀察點位移值趨于穩定，但局部最大應力難以收斂，見表2.

于是嘗試給出了含圓角過渡(半徑r=20,40 mm)的模型，如圖8所示.計算結果見表3.結果發現：① 圓角存在時，隨著網格的逐步加密，局部應力更易趨于穩定，故能較好地解決應力集中問題；② 圓角半徑越大，局部應力水平越低，觀察點位移越大.

通過2D與3D模型計算結果的比較，不難發現：① 無倒角模型存在局部應力集中，Mises應力和切應力對網格尺寸、形狀敏感性較強，難以橫向比較；② 倒角相同的3D和2D模型，其觀察點處位移趨近，誤差在 1.5% 左右，并且3D模型位移較大；③ 隨著網格的細化，3D和2D模型的位移都呈現出減小的趨勢.

圖7 局部網格加密的2D模型Fig.7 Local grid refined 2D model

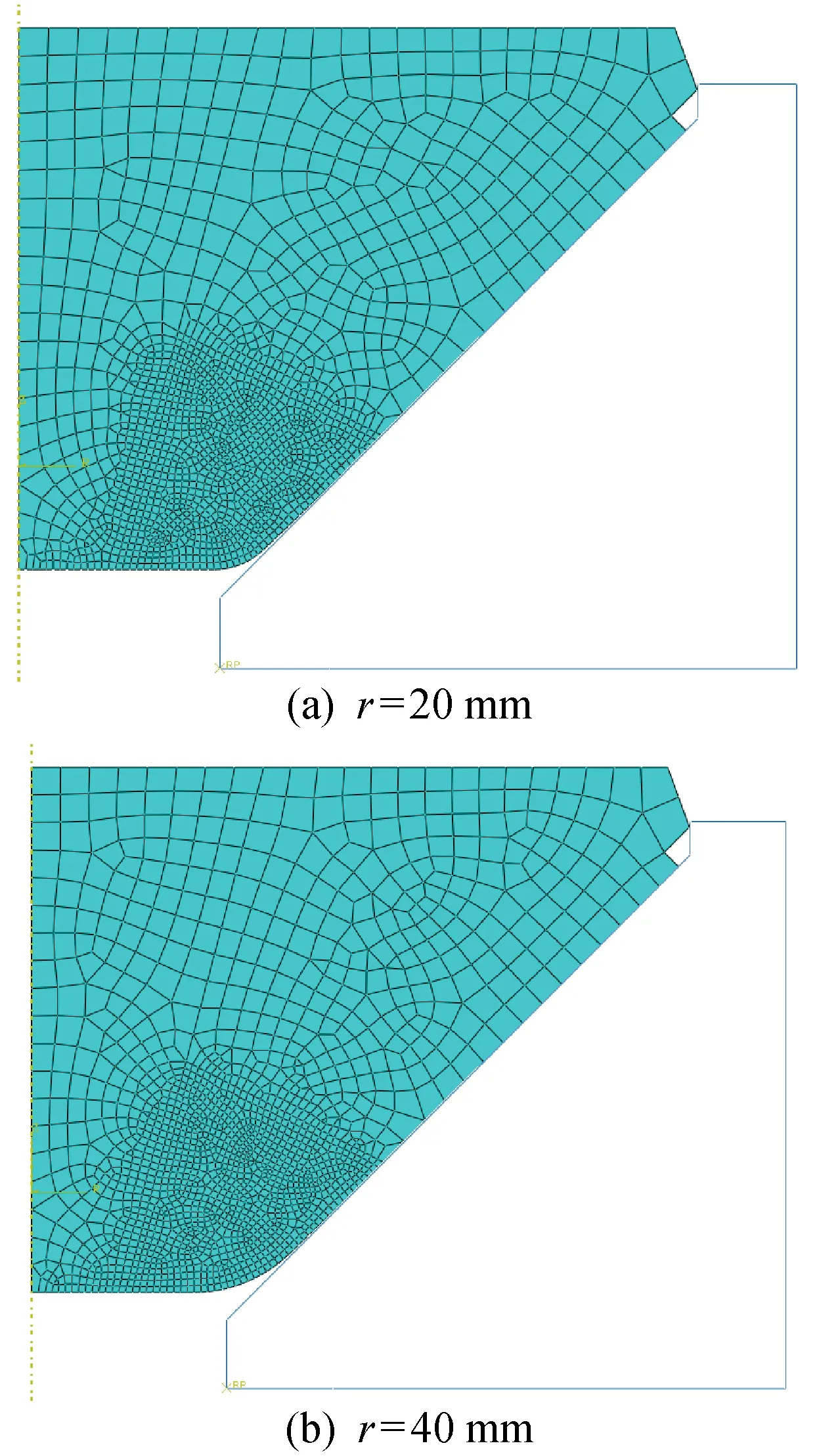
圖8 含圓角過渡的2D模型網格Fig.8 Filleted 2D model mesh

表2 無圓角2D模型在不同網格密度下的應力及位移Tab.2 Stress and displacement of none-filleted 2D model with different mesh densities

表3 存在圓角時2D模型在不同網格密度下的應力及位移
Tab.3 Stress and displacement of 20 mm-filleted 2D model with different mesh densities

r/mm網格尺寸/mmσ/MPaτ′12/MPau/mm202.0143.475.03-4.5401.0129.171.61-4.4310.5131.974.17-4.4250.2133.475.98-4.4200.1133.876.17-4.419402.0117.264.03-4.6831.0121.568.82-4.6790.5122.770.00-4.6670.2123.570.37-4.6620.1123.770.51-4.661

因此，為了節省計算資源，使用由較粗網格的3D和2D模型計算得到的觀察點位移是偏安全的，且誤差在可以接受的范圍內.為了與實驗相匹配，以下有限元建模都采用無倒角模型.

3 有限元計算及實驗結果比較

根據文獻 [8] 的實驗描述，有限元建模時，設加壓時長為 4.0×103s，且為準靜態加載，當壓力爬升至115 MPa時開始保載狀態，保載時長 1.8×105s.為了加快計算，本例中采用質量縮放技術和等效時長方法.質量縮放是指通過增加非物理質量到模型單元上從而獲得大的顯式時間步長的技術，對于不計應變率的準靜態加載問題，采用質量縮放系數加快計算是有效的手段[11].等效時長方法，是基于準靜態加載的特點，對黏彈性松弛時間參數和加載-保載時間同時除以103，使得在較短的時間步內求得位移變形歷程，而不改變位移變形的大小.

3.1 線彈性模型

基于線彈性本構關系的有限元分析，不計加載-保載時間的影響，難以反映觀察窗在高壓加載-保載過程中的蠕變變形.據此校核觀察窗位移及由此帶來的密封問題，會對觀察窗產生的位移和變形估計不足.實驗數據和有限元計算結果的比較如圖9所示，無論采用顯式動力計算還是隱式靜力計算，基于線彈性模型得到的位移結果都明顯小于實測數據.

圖9 線彈性2D模型的位移曲線Fig.9 Displacement curves of linear elastic 2D model

3.1.1線彈性模型的誤差分析 由圖9不難看出，線彈性模型在反映PMMA變形方面存在較大誤差，主要原因有：① 加載過程中，隨著壓力增大，蠕變效應產生的位移越來越重要，線彈性模型由于忽略加載過程中的蠕變位移，將產生顯著的誤差；② 在保載階段，由于載荷維持不變，線彈性模型的位移保持不變，但實驗中PMMA會繼續發生蠕變變形.

3.1.2顯式動力學計算的準確性和穩定性 采用Abaqus的顯式動力學模塊進行計算，分別考察計算結果的準確性和穩定性.

比較圖9中顯式動力學、隱式靜力學的位移曲線可知，兩者誤差很小.據此認為，使用質量縮放系數加速的顯式動力學分析可得到準確的計算結果.

一般認為，若模型動能與內能之比小于5%則計算結果穩定[11].取質量縮放系數為1×103進行有限元計算，得到模型能量(W)如圖10所示.計算過程中，模型動能的數量級從10-5下降到10-9，除了在加載開始極短的時間內，模型的動能與內能之比均遠小于5%，可認為顯式動力計算結果穩定.

圖10 模型的內能和動能Fig.10 Internal energy and kinetic energy for model

3.2 黏彈性模型

3.2.1黏彈性參數 Luo等[12]對PMMA進行了一系列不同溫度和應力水平下的較長時間的蠕變實驗，并提出了時間-溫度-壓力等效性理論.本文通過分析蠕變實驗數據，推導出基于Abaqus線性黏彈性的Prony級數參數，據此開展有限元動態分析.

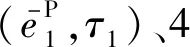
圖11 Prony級數曲線與蠕變實驗數據比較Fig.11 Prony series curves compared with creep test data

大量蠕變實驗結果表明：在較低應力水平和較低溫度下，松弛效應將放緩，即松弛時間參數將變大.由于文獻[12]中蠕變實驗所采用的應力普遍低于觀察窗中主要的分布應力，且其實驗溫度也低于觀察窗實驗的環境溫度，故需要適當調整黏彈性參數，尤其是要縮短松弛時間參數，以得到與觀察窗實驗數據較吻合的結果.

依據式(9)，在恒定泊松比下，彈性模量與切變模量、體積模量呈現等比例關系，所以彈性模量的Prony級數參數可以作為Abaqus中切變模量和體積模量的輸入參數.運用等效時長法處理后，得到如表4所示的Prony級數參數.據此，瞬時彈性模量E(t)滿足

(14)

式中：E0=2.76 GPa為初始時刻彈性模量.

表4 用于有限元分析的Prony級數參數Tab.4 Prony series parameters for FEM analysis

3.2.2計算結果分析 圖12為不同質量縮放系數(ζ)下2D和3D模型的計算結果與實驗數據的對比.可見，其他條件相同時，2D與3D模型的位移相當接近.總的來說：在加載階段，各個模型與實驗結果吻合良好；而在保載階段，ζ= 1×104時的計算結果與實驗值吻合得更好.

圖12 黏彈性模型顯式動力計算位移Fig.12 Displacement of viscoelastic model using explicit dynamic FEM

3D模型相比2D模型位移偏大的可能原因：① 2D 模型的窗座采用剛體單元，而3D模型的窗座則用實體單元來模擬，窗座變形會導致位移偏大；② 在顯式動力學計算中，時間差分會導致計算誤差，3D模型的單元數量遠多于2D模型，這種誤差會更加明顯，表現為位移值偏大；③ 對于一個軸對稱的實體模型，即使受到軸對稱的外載荷和約束，其在不同軸截面上的有限元計算結果仍會略有差異，顯式動力學計算尤其如此，在黏彈性效應更明顯的保載期間，截面差異會加大這種計算誤差.

從安全性角度出發，考慮到PMMA材料非均勻等變動因素，建議在模擬計算時預留位移冗余.因此，3D模型的計算結果雖與實驗結果有一定偏差，但在觀察窗設計中，仍然具有較高的參考價值.

4 結論

針對用傳統線彈性方法模擬深潛器觀察窗蠕變變形的困難，引入黏彈性本構模型.通過 PMMA 蠕變實驗獲取Prony級數參數并加以改進，同時基于顯式動力學有限元分析法，得到了與觀察窗加壓-保載實驗較吻合的變形結果.主要結論如下：

(1)沒有倒角的觀察窗模型，局部應力很大，易發生裂紋破壞.該處的應力計算結果難以收斂，不利于開展有限元分析.建議對觀察窗底面和側面交界處施以倒角過渡，以有效降低局部應力.

(2)針對高應力、逐步加壓的作業環境，PMMA在加載階段就已經表現出黏彈性行為，所以有必要在整個加壓-保載過程中考慮黏彈性效應.據此進行有限元計算分析，其結果更符合實際.

(3)本文有限元計算所采用的線性黏彈性模型還不能準確地反映PMMA在不同壓力水平下的非線性黏彈性行為，后續將開展進一步的研究.