2018年高考數(shù)學創(chuàng)新型試題的背景*

趙思林 柴文斌

四川省內(nèi)江師范學院數(shù)學與信息科學學院 (641112) 黃成世四川省遂寧中學 (629000)

我國高考數(shù)學歷來重視對基礎(chǔ)知識、基本技能、基本數(shù)學思想的考查．《普通高中數(shù)學課程標準(2017年版)》(以下簡稱新課標)在《學業(yè)水平考試與高考命題建議》中明確要求：“重點考查學生的思維過程、實踐能力和創(chuàng)新意識．”[1]教育部考試中心也強調(diào)“從測量考生的發(fā)展性和創(chuàng)造性入手，突出推理論證能力、應(yīng)用意識和創(chuàng)新意識的考查．”[2]因此，考查創(chuàng)新意識是高考數(shù)學命題基本原則之一，是高考數(shù)學命題的重要任務(wù)．創(chuàng)新型試題是考查學生創(chuàng)新意識最好的題型之一．高考數(shù)學創(chuàng)新型試題是指從測量考生的發(fā)展性和創(chuàng)造性著手突出能力考查的新穎問題[2]．高考數(shù)學創(chuàng)新型試題一般都有深刻的背景，如教材背景、高等數(shù)學背景、實際應(yīng)用背景、新課程改革背景、數(shù)學文化背景等．

1.教材背景

數(shù)學“四基”(基礎(chǔ)知識、基本技能、數(shù)學基本思想和數(shù)學活動經(jīng)驗)是實現(xiàn)數(shù)學創(chuàng)新的必要基礎(chǔ)．數(shù)學的創(chuàng)新離不開“四基”，“四基”離不開教材．教材是高考數(shù)學試題的創(chuàng)新之源．由教材編擬創(chuàng)新型試題是高考命題的常用方法，是高考命題智慧的體現(xiàn)．從高考試題的題源來看，教材是試題的主要來源，是高考命題的基本依據(jù)和出發(fā)點，歷年高考試卷中都有一些試題直接出自于教材或由教材上的例、習題改編而成．高考命題重視由教材的知識、例題、習題生成試題，既可保證試題的公平性，又對抑制題海戰(zhàn)術(shù)有一定的積極作用，對中學數(shù)學教學有良好的導(dǎo)向作用．

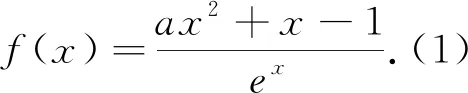
點評：本題第(1)問在人教A版教材選修2-2第一章第二節(jié)《導(dǎo)數(shù)的計算》習題A、B組(第18、19頁)都能找到根基，而對于第(2)問筆者發(fā)現(xiàn)本題是以ex≥1+x，當且僅當x=0取等為背景立意的，而這正是人教A版教材選修2-2第一章第三節(jié)《導(dǎo)數(shù)在研究函數(shù)的應(yīng)用》習題B組1題(第32頁)中的一個選項，可以說命題人牢牢抓住以教材為中心，體現(xiàn)了高考題來源于教材，符合新課標2017版的基本理念．下面就這一背景對本題第(2)問給一種更加優(yōu)化解答．

解：(2)在ex≥1+x中，令x=t+1代入得et+1≥2+t，即-et+1≤-(2+t)．而ax2+x-1≥-ex+1等價于ax2+x-1≥-ex+1，即等價于ax2+x-1+ex+1≥0．當ax2+x-1+ex+1≥x2+x-1+x+2=(x+1)2≥0時，有ax2+x-1+ex+1≥x2+x-1+x+2=(x+1)2≥0．所以f(x)+e≥0．

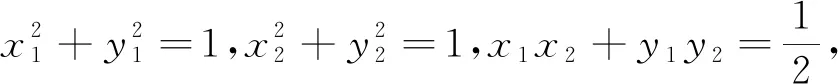
點評：通過探究可以發(fā)現(xiàn)，本題問題的實質(zhì)是平面內(nèi)一個正三角形在繞著一個頂點旋轉(zhuǎn)，而研究另兩個頂點到定直線的距離之和的最大值，而這樣一個問題恰好與人教A版教材必修4第三章第二節(jié)《簡單的三角恒等變換》復(fù)習參考題A組13題(第147頁)所運用的數(shù)學模型一樣，基于此，我們采用教材的解題思路就可以得到一種更加優(yōu)化的解題方法，如下：

圖1

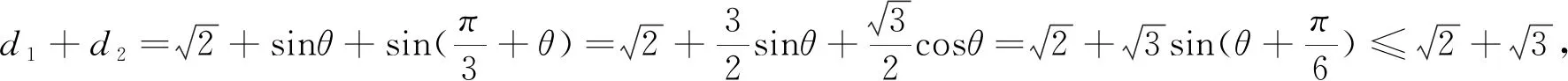
2.高等數(shù)學背景

高等數(shù)學的一些基本思想和基本概念為設(shè)計創(chuàng)新型試題提供了廣闊而又深刻的背景，這是因為以高等數(shù)學為背景的試題能有效考查學生學習的潛能．許多高考創(chuàng)新型試題都有比較深刻的高等數(shù)學背景，這類題目立意深遠、形式新穎，在平常教學中很少碰到．

例4 (2018年全國卷Ⅲ理科第21題)已知函數(shù)f(x)=(2+x+ax2)ln(x+1)-2x．

(1)若a=0，證明：當-10時，f(x)>0；

(2)若x=0是f(x)的極大值點，求a．

利用極限的保序性以及洛必達法則，可得

點評：本題第(2)問以鄰域的定義以及洛必達法以及數(shù)學極限為背景，主在培養(yǎng)學生自主學習的精神，以及超前學習的意識．

3.實際應(yīng)用背景

廣泛的應(yīng)用性是數(shù)學的基本特點之一．數(shù)學的應(yīng)用價值體現(xiàn)在它的工具性和應(yīng)用性上．數(shù)學來源于生活，又能解決實際生活中的很多實際問題．因此，高考命題重視對實際應(yīng)用問題的考查．實際應(yīng)用題是對考生“綜合實力”的考查，是考查數(shù)學抽象、數(shù)學建模、數(shù)學運算、數(shù)據(jù)分析等核心素養(yǎng)的良好題型，也是考查數(shù)學創(chuàng)新意識的良好題型．

圖2

例5 (2018年江蘇卷第17題)某農(nóng)場有一塊農(nóng)田,如圖2所示,它的邊界由圓O的一段圓弧MPN(P為此圓弧的中點)和線段MN構(gòu)成,已知圓O的半徑為40米，點P到MN的距離為50米,先規(guī)劃在此農(nóng)田上修建兩個溫室大棚，大棚Ⅰ內(nèi)的地塊形狀為矩形ABCD．大棚Ⅱ內(nèi)的地塊形狀為△CDP，要求AB均在線段MN上，C,D均在圓弧上,設(shè)OC與MN所成的角為θ．(1)用θ分別表示矩形ABCD和△CDP的面積,并確定sinθ的取值范圍；(2)若大棚Ⅰ內(nèi)種植甲種蔬菜，大棚Ⅱ內(nèi)種植乙種蔬菜,且甲、乙兩種蔬菜的單位面積年產(chǎn)值之比為4∶3．求當θ為何值時，能使甲、乙兩種蔬菜的年總產(chǎn)值最大．

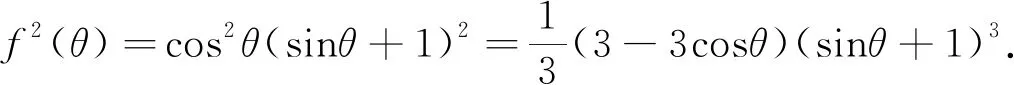
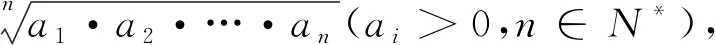
點評：本題以生活中溫室大棚為背景考查了三角函數(shù)的應(yīng)用，第一問主要是建立一個角度模型值得注意的是角的定義域或者范圍，第二問主要是三角函數(shù)最值問題，值得一提是第二問恰好與2018年全國卷Ⅰ理科第16題出現(xiàn)驚人的相似，它們所運用的解題方法是導(dǎo)數(shù)法、均值不等式法等，可以說今年命題人側(cè)重對三角函數(shù)的熱衷考查．應(yīng)用題的步驟一般有兩步：一是將實際問題轉(zhuǎn)化為數(shù)學問題；二是利用數(shù)學內(nèi)部的知識解決問題．

4.新課程改革背景

近幾年，一些創(chuàng)新型試題命制的價值取向體現(xiàn)新課標精神，比如，新課標非常重視數(shù)學探究、數(shù)學建模，提倡考開放性問題．因此，近年出現(xiàn)了不少以數(shù)學探究、數(shù)學建模、開放性問題為背景的新題好題．

(1)數(shù)學探究

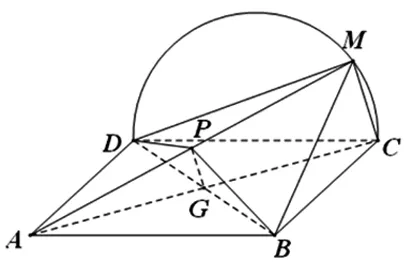
圖3

分析：(1)分析從略．對于(2)，探索能否在線段AM上找到一點P，使得MC和平面PBD中一條直線平行.不妨在線段AM上任意取一點P，則平面PBD與平面AMC的交線為PG，通過探究發(fā)現(xiàn)：當P點為線段AM的中點時，即PG為△AMC的中位線，如圖所示，那么易證MC∥平面PBD.

點評：本題主要考查空間想象能力、邏輯推理能力和數(shù)學探究意識，還考查應(yīng)用向量知識解決數(shù)學問題的能力，反映了考生理性思維的廣度和深度，體現(xiàn)了自主學習和主動探究的精神，呈現(xiàn)出研究性學習的特點，有利于啟發(fā)和培養(yǎng)學生邏輯思維的能力．

此外，2018年全國卷Ⅰ文科第17題在所求數(shù)列中加入了討論,通過層層遞進、逐步深入的設(shè)問展現(xiàn)了思維的過程,充滿了探究的味道,體現(xiàn)了新課標研究型學習的理念；2018年上海卷第21題提出“接近”數(shù)列這一新的概念，需要學生在自主學習的基礎(chǔ)上進行探索、研究，形成解決問題的策略與表達．

(2)開放性問題

開放性問題是新課標大力提倡的創(chuàng)新型試題．

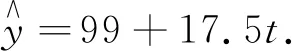
圖4

(1)分別利用這兩個模型，求該地區(qū)2018年的環(huán)境基礎(chǔ)設(shè)施投資額的預(yù)測值；(2)你認為用哪個模型得到的預(yù)測值更可靠？并說明理由．

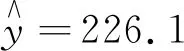
(2)利用模型②得到的預(yù)測值更可靠．其理由是不唯一的，從略．

點評：本題以環(huán)境基礎(chǔ)設(shè)施投資為背景,第二問的理由說明不唯一，體現(xiàn)了結(jié)論的開放性.考查概率統(tǒng)計中的線性回歸模型、折線統(tǒng)計圖等基礎(chǔ)知識，以及數(shù)據(jù)立意與分析、數(shù)學運算、統(tǒng)計評價等數(shù)學素養(yǎng)．此外，2018年北京卷文科第11題、理科第13題以舉例的形式開放，考查知識的形成過程，引導(dǎo)課堂教學更加注重過程和方法.

5.數(shù)學文化背景

數(shù)學是一門充滿創(chuàng)新的科學，也是人類文化的精華．數(shù)學文化既崇尚創(chuàng)新，又強化育人．數(shù)學文化是立德樹人的有效載體．數(shù)學文化在立德樹人的過程中具有春風化雨、潤物無聲的巨大作用．

例8 (2018年上海卷第15題)《九章算術(shù)》中，稱底面為矩形而有一側(cè)棱垂直于底面的四棱錐為陽馬，設(shè)AA1是正六棱柱的一條側(cè)棱，如圖5，若陽馬以該正六棱柱的頂點為頂點、以AA1為底面矩形的一邊，則這樣的陽馬的個數(shù)是( )．

A．4B．8C．12D．16

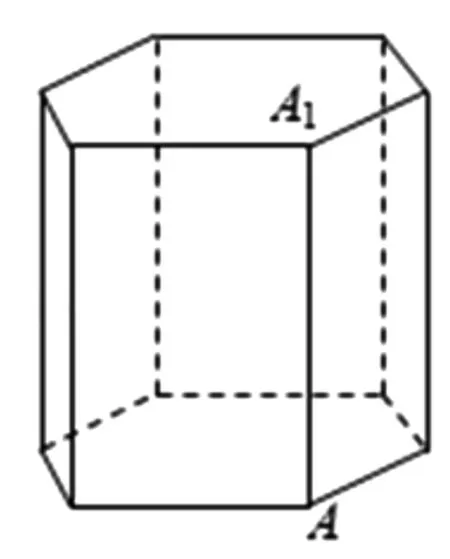
圖5

分析：如圖6所以，當另一條取邊BB1時，頂點可取D1,D,E1,E，共4個點；當另一條取CC1時，頂點可取F1,F,D1,D，共4個點；當另一條取DD1時，頂點無可取，共0個點；當另一條取EE1時，頂點可取B1,B,D1,D，共4個點；當另一條取FF1時，頂點可取C1,C,D1,D，共4個點，綜上所述，共存在4+4+0+4+4=16個“陽馬”.

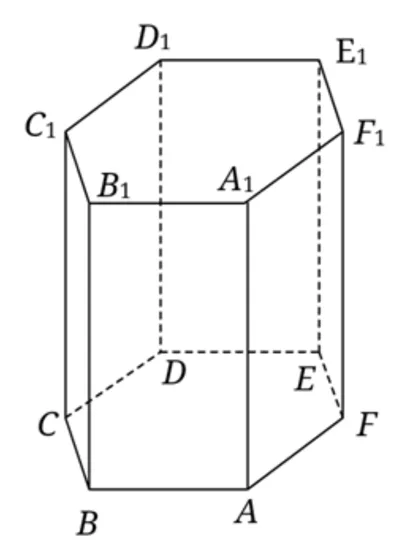
圖6

點評：本題的創(chuàng)作靈感來自于《九章算術(shù)》它是中國古代最著名的傳世數(shù)學著作，它的出現(xiàn)標志著中國古代數(shù)學形成了完整的體系．本題以《九章算術(shù)》中陽馬的概念為背景考查了立體幾何中的棱柱與棱錐，設(shè)計思路新穎．試題將數(shù)學文化有機地融入試題，對于弘揚中國傳統(tǒng)文化，樹立文化自信，很有現(xiàn)實意義．

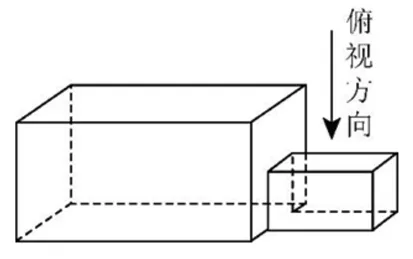
圖7

例9 (2018年全國卷Ⅲ理科第3題)構(gòu)件右邊的小長方體是榫頭．若如圖7擺放的木構(gòu)件與某一帶卯眼的木構(gòu)件咬合成長方體，則咬合時帶卯眼的木構(gòu)件的俯視圖可以是( )．

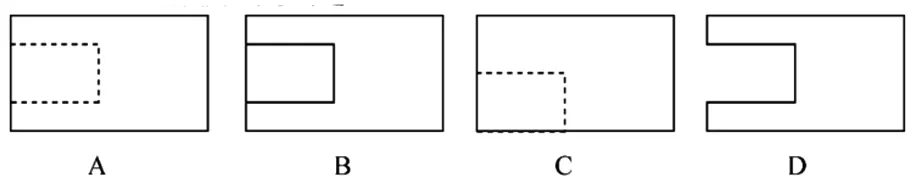
點評：本題以中國古建筑借助榫卯(凸出部分叫榫頭，凹進部分叫卯眼)連接木構(gòu)件為背景，很好的命制了一道三視圖試題，此題的難度雖不大，但試題的背景材料非常新穎，展示了數(shù)學文化的魅力．考生需要先觀察卯眼的直觀圖，再想象其俯視圖，這和以往多數(shù)通過所給三視圖想象直觀圖的命題方式相比，不僅了增添了一些新意，而且也傳播了中國悠久的文明和智慧．這種以我國古建筑為背景的試題，使考生受到數(shù)學文化的教育，對于激發(fā)考生的民族自豪感，學習數(shù)學家的探索精神是有益的．

此外，2018年北京卷理科第4題以音樂中的“十二平均律”為背景，有機的將我國古代音律方面的成就與數(shù)學中的等比數(shù)列概念結(jié)合在一起，同時還考查了指數(shù)運算；2018年全國卷Ⅰ理科第10題以古希臘數(shù)學家研究的幾何圖形為情境，設(shè)計了一個幾何概型及幾何概率計算的問題．