問題導引 自然探究*
——蘇教版五下《圓的認識》教學實錄與思考

古希臘畢達哥拉斯學派認為，一切平面圖形中最美的是圓形。從數(shù)學家的角度看，圓的美可能不僅指美學意義上的平衡、對稱、和諧、圓滿等，還在于圓較之其他圖形蘊含著更為豐富的知識內(nèi)容，涉及更多數(shù)學對象，對數(shù)學發(fā)展的作用更大。從小學數(shù)學教學的角度看，圓是小學階段學習的第一個由曲線圍成的圖形，它對學生的發(fā)展價值有別于由直線圍成的幾何圖形。所以，它是進行數(shù)學教學研究的一座富礦，許多數(shù)學教師都用它來展示自己的教學理念、教學主張。本節(jié)課以蘇教版教材為依據(jù)，在借鑒既有研究成果的基礎(chǔ)上確立自己的教學思路，即以問題導引，讓學生自然地探究。

【教學過程】

一、引入

（課件出示蘇教版五下第87頁《你知道嗎》欄目的圖片。）

師：這些現(xiàn)象、物體和運動中隱藏著一種同樣的圖形，它是什么圖形？

生：圓形。

師：今天，我們就一起來認識圓。（板書：圓的認識）

利用教材《你知道嗎》欄目中的生活內(nèi)容引入圓，簡潔高效。

二、探究

1.畫圓：探究圓的特征。

（1）在比較中初步認識圓

師：我們以前學過哪些平面圖形？

生：長方形、正方形、三角形……

師：圓形與它們相比有什么相同和不同之處？

生：它們都是由線圍成的圖形。不同的是圓沒有角，邊是彎曲的；長方形、正方形都有角，邊是直的。

師：說得真好！圓是由彎曲的線圍成的圖形。（在黑板上隨手畫一條彎曲線）這條曲線是不是我們隨便畫的彎曲線呢？

生：不是隨便畫的。

（2）自主畫圓

師：你能畫出一個圓嗎？你打算怎樣畫？

（學生畫圓，教師巡視。）

師：你是怎么畫的？誰來介紹一下？

（學生有照著一個圓片描出來的，有拉線移動畫的，有用圓規(guī)畫的，有直接用手畫的……教師選擇隨手畫、照樣子描、線栓筆畫、圓規(guī)畫四種情況展示。）

師：這幾種方法你喜歡哪一種？為什么？

生：我喜歡照樣子描，這樣最簡單，畫得很標準。

師：這種畫法有沒有不好的地方？

生：它只能畫這么大，不能任意改變大小。

師：有沒有人喜歡別的方法？

生：我喜歡用圓規(guī)畫圓，這樣最方便、最標準，而且可以任意改變大小。

師：大家都這么認為嗎？（生紛紛點頭）哈，都是這樣看，我也是這樣認為的。圓規(guī)就是專門用來畫圓的，用它可以標準、便捷、任意改變大小地畫圓。有沒有人喜歡這種用線拴著筆，然后移動筆畫圓的？（生紛紛搖頭）沒有？大家為什么不喜歡？

生：太麻煩了，還要用手按著中間，而且稍微動一下就不標準了。

師：有道理！那這種方法有沒有優(yōu)點呢？

（教師點擊課件，播放學生在操場上畫大圓的視頻。）

生：拉長線可以畫比較大的圓。

師：看來每種方法都有優(yōu)缺點。照樣子描比較省事，但不能任意改變大小；用拉線的方法可以畫比較大的圓，但沒有圓規(guī)方便；用圓規(guī)畫圓比較便捷而且標準，但不能畫得很大；隨手畫的圓不標準，但省事，在畫示意圖的時候也可以用。所以，凡事要一分為二地看。

師：請大家說說，用圓規(guī)畫圓時要注意什么？

生：要把圓規(guī)兩腳分開，定好兩腳間的距離。有針尖的腳要固定在一點上，旋轉(zhuǎn)圓規(guī)時兩腳間的距離不能變。

師：好，請大家按照剛才說的，用圓規(guī)在練習本上畫一個圓。

（3）介紹圓規(guī)畫法和圓心、半徑、直徑

師：老師也用圓規(guī)畫了一個圓，請看，中心這個點叫什么？

生：圓心。

師：對，叫圓心，通常用字母O表示。關(guān)于圓，你還知道哪些名稱？

生：我還知道半徑和直徑。

師：你能上來畫一下嗎？

（學生上黑板畫，教師標注：半徑r、直徑d。）

師：仔細觀察半徑與直徑，你能發(fā)現(xiàn)什么？

生1：圓心是直徑的中點，直徑兩個端點都在圓上；半徑一端是圓心，另一端在圓上；一個圓可以畫很多條直徑。

生2：直徑長度是半徑的2倍。

師：怎么證明？

生2：一條直徑就是兩條半徑接起來的。

師：是的，一眼就看出來了。（板書：d=2r）還有別的發(fā)現(xiàn)嗎？

生3：直徑是圓上兩點間最長的線段。

師：這是什么意思？你解釋一下。

生3：就是在圓上不管你怎么畫線段都不會比直徑長。

師：這是真的嗎？你怎么證明？

（學生上黑板，在圓上畫線段，并解說：你可以隨便測量一條線段的長度，它都沒有直徑長，最多和直徑一樣長。）

師：確實是這樣。

（教師演示課件，解說圖1。板書：直徑是圓上兩點間最長的線段。）

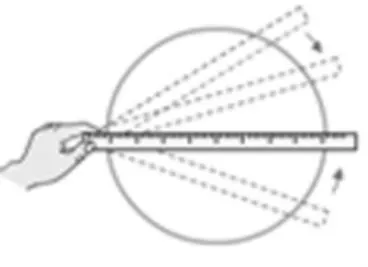
（圖1）

師：大家還有什么發(fā)現(xiàn)？

生4：直徑是圓的對稱軸，沿著直徑對折，兩邊能重合。

師：哈，你不僅發(fā)現(xiàn)直徑是對稱軸，而且給出了理由。真棒！（板書：對稱軸）

師：你能用圓規(guī)畫一個直徑為5厘米的圓嗎？請標出 O、r、d。

（展示點評學生所畫的圓。）

通過與由直的線段圍成的圖形進行比較，凸顯圓是由曲線圍成的圖形的特點。直邊圖形可以用直尺來畫，那圓這個由曲線圍成的圖形怎么畫呢？這個疑問自然地出現(xiàn)了，畫圓的需要也就產(chǎn)生了。教師放手讓學生用自己喜歡的方式畫圓，然后分析各種方法的優(yōu)缺點，幫助學生辯證地看待事物。利用學生既有的知識經(jīng)驗，引出半徑和直徑，通過聚焦圓的半徑和直徑來探究圓的特征。

2.套圓：深化理解特征。

（1）自主嘗試在小圓外套畫一個大圓

師：我這兒有個小圓，是照一個圓片描出來的，你能在它外面畫一個大一點的圓正好把它套在正中間嗎？

（學生獨立解決，教師巡視，選擇學生的作業(yè)（如圖2）進行展示。）

（圖2）

師：大家仔細觀察，你覺得這位同學畫的大圓正好把小圓套在正中間了嗎？

生：有一點偏。

師：怎樣才能將小圓套在正中間呢？小組討論討論。

（2）小組合作找圓心

師：哪個小組匯報？

生：我們組是這樣做的，先畫出一條直徑，再量出它的長度是2厘米，半徑就是1厘米，所以這就是圓心。

師：噢，原來他們是先找小圓的圓心，然后畫的。大家同意他們的方法嗎？都同意？我也同意。只要找到小圓的圓心就好辦了。但是，你們怎么知道這條線段就是直徑呢？

生：因為圓上最長的線段就是直徑，我們試驗了，它就是最長的。

師：哦，你們是用剛才找直徑的方法找到的啊。其實，還有一種更快捷的方法來找直徑。

（課件演示圖 3，教師講解。）

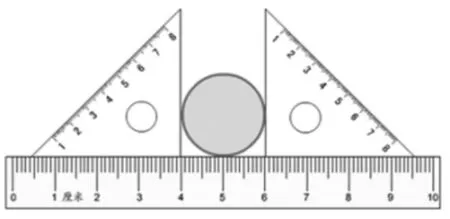
（圖3）

師：找到小圓的圓心就容易畫出外面的大圓了。兩個圓的圓心相同，我們叫它們同心圓。

本環(huán)節(jié)繼續(xù)深度認識圓的特征，這個行為不是直白地向?qū)W生提出要求，而是精心設計了一個類似游戲的任務——在未知圓心的小圓外套一個大圓來實現(xiàn)的。“套圓”任務等價于尋找圓心，等價于在圓上尋找直徑，其實質(zhì)就是直徑是圓上最長的線段，長度是半徑的2倍。“套圓”是包裹在圓知識外面的“糖衣”，使學生很想去品嘗。

三、深化

1.畫一個圓，讓 A、B 兩個點（如圖4）都在圓上。學生獨立嘗試，教師巡視指導，學生匯報。

（圖4）

師：還有不同的畫法嗎？（課件演示圖5）這些圓都是經(jīng)過這兩個點的，這些圓的排列有什么規(guī)律？

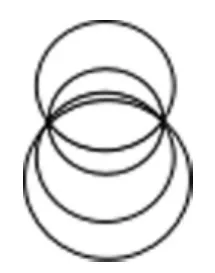
（圖5）

2.在生活中，車輪為什么要做成圓形？

生：圓形的車輪容易滾動；滾起來比較平穩(wěn)，不會上上下下的。

師：為什么圓形的車輪就比較平穩(wěn)，不會上下顛簸呢？你能用所學的知識解釋一下嗎？

生：……

師（播放課件演示）：我們在車輪上任意取A、B、C三個點（如圖6），當車輪從A點著地滾到B點或C點著地時，車輪中心O點距地面的高度會不會變化？

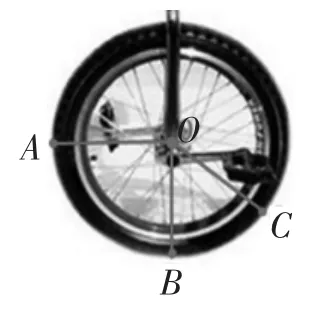
（圖6）

生：不會，高度一樣？

師：為什么？

生：OA、OB和OC是相等的，因為它們都是圓的半徑，圓的半徑都相等。

師：是的。圓的半徑都相等實際上就是說圓上的任意點到圓心的距離都相等，所以我國古代的數(shù)學家說：“圓，一中同長也。”

3.拓展：生活中的圓形物體非常多，如窨井蓋、水管橫截面等，你能用圓的一些知識來解釋解釋嗎？課后大家可以去探索研究。

【教后反思】

1.理念：化陳述為探究。

數(shù)學知識總體上可以分為陳述性知識和程序性知識兩大類，像“圓的認識”這類知識就屬于前者，教材編排這類知識時往往采用陳述的方式，具體為：呈現(xiàn)生活中的相關(guān)事物→抽象出數(shù)學圖形→介紹圖形各部分名稱→通過觀察和操作活動認識特征→練習，強化理解。一些教師在教學這類知識時，往往習慣于按照教材的方式向?qū)W生進行知識的陳述，學生則進行有意義接受學習——了解是什么、理解為什么。其實，陳述性知識也可以進行探究式教學，讓學生在主動觀察、操作、猜想、嘗試和驗證的過程中發(fā)現(xiàn)它是什么、為什么是這樣。就本節(jié)課教學而言，在學生經(jīng)歷觀察圓、畫圓、觀察和發(fā)現(xiàn)直徑、半徑及其關(guān)系的過程后，又精心設計了“套圓”環(huán)節(jié)，使學生進行了興趣盎然的探究學習。

2.實施：問題導引學生探究。

問題不僅能激發(fā)學生探究的興趣，還導引著學生的探究行為。在引入環(huán)節(jié)，以“這些現(xiàn)象、物體和運動中隱藏著一種同樣的圖形，它是什么圖形？”這一問題，讓學生從日常生活中抽象出圓的概念和圖形。探究環(huán)節(jié)設計了三個問題：圓形與由直的線段圍成的圖形相比有什么相同和不同之處？你打算怎樣畫？怎樣才能畫一個大圓將小圓套在正中間？第一個問題通過比較，讓學生發(fā)現(xiàn)圓是由曲線圍成的特征。第二個問題比較開放，讓學生開動腦筋，個性化地畫圓。對這些不同畫法的比較分析，讓學生認識到各種畫法的優(yōu)劣之處，有利于他們形成辯證的觀念。同時，在進行這些操作和比較的過程中，已經(jīng)向?qū)W生滲透了一些圓的知識，例如：圓的大小與圓規(guī)兩腳之間的距離有關(guān)，與拉的線的長度有關(guān)；用手畫圓時，鉛筆尖應圍繞著一個中心，盡量保持和中心相同的距離；等等。這些其實就是對半徑、圓心等知識的感性認識。深化環(huán)節(jié)也有三個問題：第一個問題是在探究中不斷深化學生對圓的知識的認識；第二個問題是讓學生主動運用所學知識解釋生活現(xiàn)象，這有助于發(fā)展學生在復雜的生活情境中運用知識的能力；第三題繼續(xù)拓展學生的探究活動，讓學生帶著疑問走出課堂。