常見概率分布間的極限關系

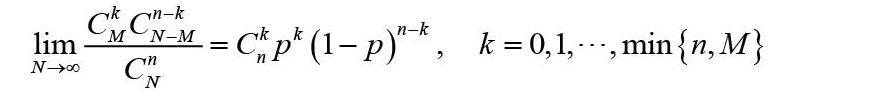
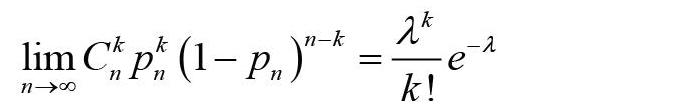
摘? 要：以定理形式給出了常見概率分布間的6種極限關系，包括超幾何分布的二項近似、二項分布的泊松近似、二項分布的正態近似、泊松分布的正態近似、t分布的正態近似和分布的正態近似。除了比較熟悉的泊松定理和棣莫佛—拉普拉斯中心極限定理外，其他定理一般文獻較少提及，或只給出結論而未加以證明，該文對這些定理均給出了證明，同時對定理的適用條件及應用進行了說明。了解以上常見概率分布間的極限關系，有助于系統理解常見分布間的聯系，同時為概率的近似計算及統計推斷提供了依據。

關鍵詞：概率分布? 極限關系? 二項分布? 泊松分布? 正態分布

中圖分類號：O211.4? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ?文章編號：1672-3791（2019）03（b）-0221-02

Abstract： In the form of theorems， six kinds of limit relations among common probability distributions are given， including binomial approximation of hypergeometric distribution， Poisson approximation of binomial distribution， normal approximation of binomial distribution， normal approximation of Poisson distribution， normal approximation of t distribution and normal approximation of? distribution. Except for the familiar Poisson theorem and Dimov-Laplace central limit theorem， other theorems are seldom mentioned in general literature， or only conclusions are given without proof. These theorems are proved in this paper. These theorems are proved in this paper， and the applicable conditions and applications of these theorems are explained. Understanding the limit relationship between the above common probability distributions is helpful for the system to understand the relationship between the common distributions， and provides a basis for approximate calculation of probability and statistical inference.

Key Words： Probability Distribution; Limit Relation; Binomial Distribution; Poisson Distribution; Normal Distribution

在概率論與數理統計這門學科中，一些常用概率分布間存在著極限關系[1]，從而將兩個隨機變量通過漸近分布聯系起來。目前多數文獻在介紹常見的概率分布時對分布間的極限關系介紹得不夠系統，而了解它們之間的這種極限關系，一方面有助于理解常見概率分布間的聯系，另一方面在概率的近似計算及參數估計、假設檢驗等統計推斷問題中有著廣泛的應用價值。以下主要討論常見概率分布間的6種極限關系。

1? 超幾何分布的二項近似

定理1? 設隨機變量，（P為常數），則n，k固定的條件下，有

證明

在實際應用中，一般地，若N較大，n相對較小（n<

以上結論也可從超幾何分布的背景來理解。設總體容量為N，其中具有某屬性的個體數為M，從總體中無放回地隨機抽取一個容量為n的樣本，則樣本中具有該屬性的樣品數服從h（n，N，M）。若總體容量N較大，而樣本容量n相對較小時，無放回抽樣可近似看作有放回抽樣，即構成一個n重的伯努利試驗，從而樣本中具有該屬性的樣品數近似服從B（n，p）。

2? 二項分布的泊松近似

定理2（泊松定理）? 設在n重伯努利試驗中，每次試驗中事件A發生的概率為Pn（與n有關），且，則有：

大多文獻都給出了該定理的證明[4]，此處不再贅述。

二項分布的計算有時候是非常繁瑣的，該定理表明，若二項分布B（n，p）中的參數n較大，p較小，而np適中（一般地0.1≤np≤10）時，則可用泊松分布來近似，其中參數。

3? 二項分布的正態近似

定理3（棣莫佛—拉普拉斯中心極限定理）? 設μn為n重伯努利試驗中事件A發生的次數，且每次試驗中事件A發生的概率為p（0

大多文獻也都給出了證明[5]，該定理的證明只需利用林德伯格—勒維中心極限定理即可容易得出。

棣莫佛—拉普拉斯中心極限定理是歷史上第一個中心極限定理，定理中的μn-B（n，p），而當n充分大時，二項分布B（n，p）可用正態分布N（np，np（1-p））來近似。

由于二項分布是離散分布，正態分布是連續分布，故在應用該定理進行近似計算時，往往需要做一些修正，從而提高計算的精度。

例如計算P（m≤μn≤n）時，先做修正P（m≤μn≤n）=P（m-0.5<μn

泊松定理表明了在一定的條件下，二項分布也可利用泊松分布來近似，那么需要考慮二項分布的泊松近似和正態近似的不同適用場合。一般而言，在P較小時用泊松分布近似的精度較高，而在np>5和n（1-p）>5時用正態分布近似效果較好。

4? 泊松分布的正態近似

定理4表明，若泊松分布的P（λ）參數λ較大時，可用正態分布N（λ，λ）來近似泊松分布。但由于是用連續分布來近似離散分布，故在計算時可能需要做適當的修正。

t分布的概率密度圖像關于縱軸對稱，與標準正態分布的概率密度圖像形狀上相似，但t分布的圖像峰要低一些，兩側的尾部要大一些。而當自由度n較大（一般地n≥30）時，t分布可用標準正態分布來近似。

6? 分布的正態近似

7? 結語

以上討論了常見概率分布間的6種極限關系，其中第1、2種情況都是用離散分布來近似離散分布，第5、6種情況都是用連續分布來近似連續分布，而第3、4兩種情況是用連續分布來近似離散分布，在應用過程中可能需要做一些修正，從而提高近似計算的精度。同時注意到后4種情況的極限分布均為正態分布，這也從一個側面說明了在自然界及社會現象中為什么大量的隨機變量都服從或近似服從正態分布。

參考文獻

[1] 侯文.常見概率分布間的關系[J].遼寧師范大學學報：自然科學版，2005，28（4）：503-505.

[2] 付安民.超幾何分布與二項分布的有機聯系[J].岳陽師范學院學報：自然科學版，2003，16（1）：46-48.

[3] 聶凡皓.與二項分布相關的極限定理[J].課程教育研究，2018（30）：119-120.

[4] 茆詩松，程依明，濮曉龍.概率論與數理統計教程[M].2版.北京：高等教育出版社，2011：98-99.

[5] 盛驟，謝式千，潘承毅.概率論與數理統計[M].4版.北京：高等教育出版社，2008：123-124.①作者簡介：李玲（1980—），女，漢族，安徽廬江人，碩士，講師，研究方向：可靠性統計。