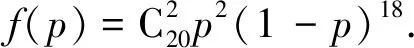代換法在高中數學解題中的應用

安徽天柱山旅游學校

徐景瑜 (郵編：246300)

在高中數學教學中，解決問題是十分重要的一個環節，由于高中數學本身對學生的邏輯思維能力要求比較高，導致很多學生面對一些數學問題會產生無從下手的感覺，這就會對學生的實際學習效果產生極大影響，同時也降低了學生的考試成績.代換法是當前高中數學解題中應用比較常見的一種方法，其可以幫助學生將復雜、抽象的數學問題轉變成簡單、形象的問題，能極大的幫助學生解決數學問題，有助于學生學習能力提升.

1 代換法的相關概述

代換法是高中數學解題中比較常見的一種方法，學生在解決高中數學問題時，經常會遇到各種復雜存在的數學題，這些題目中有兩個，甚至是多個未知條件，而代換法的應用可以幫助學生更好地理清各個條件之間的相互關聯，并對題目中的數量關系進行恰當轉化，結合各種變量的條件轉換，將一種問題求解轉變成另一種問題的求解，從而簡化了解題思路，降低了學生的解題難度.

在實際中，代換法的表現形式有很多，常見的有三角函數代換、變量代換、函數代換、等量及不等量代換、圖形代換等，在具體的解題過程中，需要結合題目信息，進行靈活的代換，這樣才可以真正的發揮出代換法的解題優勢.在高中數學教學中，教師在引導學生學習代換法這種解題方法時，其核心在于對問題進行轉換，同時在具體的實施中需要對以下幾個問題加以討論：(1)高中數學的各個板塊是邏輯相通的，采用代換法時，需要進行全方面考慮，解題思維不能局限在一個方向，如換元法屬于代換法的具體表現，但是代換法可以進行換元法以外的其他途徑轉變，如數形轉變，所以要結合題目已知信息進行靈活的代換；(2)在代換的過程中，不能被問題導向左右思維，需要學生結合題目的信息，進行發散性思考，這樣才可以發揮出代換法的優勢；(3)在考慮問題的解決方法時，不能單純地考慮某一種方法，需要與其他方法結合起來，這樣才可以保證解題思維更加明確、清晰.

2 代換法在高中數學解題中的應用

2.1 圖形代換的應用

圖形代換是一種十分常見的代換模式，其多用于方程問題中，很多時候學生在求解方程問題時，會感覺題目中給出的信息十分繁雜，無法從中整理出有用的信息，這就會影響到學生的解題準確性.對此，在實踐教學中，高中數學教師可以引導學生采取圖形代換的解題方法，將相關方程問題轉變成圖形問題，從圖形的角度來思考方程，并指引學生將相應的圖形畫出來，讓學生可以通過直觀的圖形來解決實際問題.

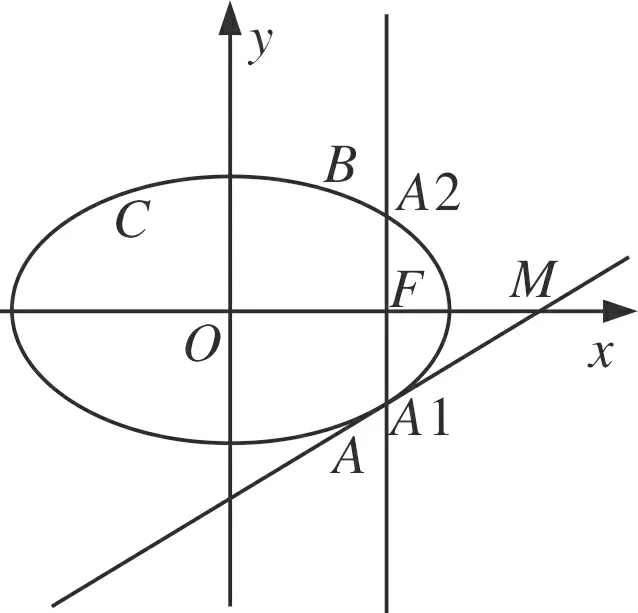
圖1

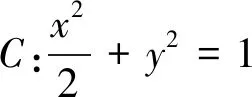
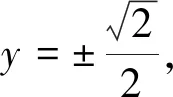
在求解(2)時，也需要結合(1)做出的圖形進行：

當l與x軸重合時，∠OMA=∠OMB=0°；

當l與x軸垂直時，OM為AB的垂直平分線，所以∠OMA=∠OMB；

當l與x軸不重合也不垂直時，設l的方程為y=k(x-1)(k≠0)，A(x1,y1),B(x2,y2)，

由y1=kx1-k,y2=kx2-k，得

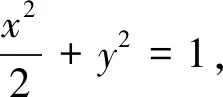
(2k2+1)x2-4k2x+2k2-2=0.

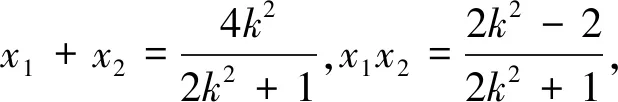
則2kx1x2-3k(x1+x2)+4k

從而kMA+kMB=0，故MA、MB的傾斜角互補，所以∠OMA=∠OMB.

對于這類綜合性問題，題目給出的已知信息比較有限，但是隱藏的信息卻比較多，為了讓學生可以更好地將題目中的信息充分挖掘出來，順利地進行解題.高中數學教師就可以引導學生采取圖形代換的方法，把理論性的問題轉變成形象的圖形問題，根據題目中的信息，畫出相應的圖形，對圖形進行思考、解答，這樣就可以讓學生更好地打開思路，有助于學生解題效率提升.

2.2 三角代換法的應用

在高中數學解題中，三角代換具有很廣泛的應用，其解題模式比較靈活，其通過將代換法在三角函數中的具體應用，能將一些復雜的代數問題進行簡單化處理，實現了代數表達向三角表達的轉變，達到了簡化題目、明確解題思路的效果.

例2一條直線過點P(3，2)與,x、y軸的正半軸交于A、B兩點，若ABO的面積最小(O為原點)，求此時直線的方程.

在解這個問題時，有很多學生會單純地從代數的角度進行解題，整個過程十分困難，這時教師就可以指引學生采取三角代換的方法，在本題中，可以根據已知點的坐標，將相應的方程求解出來，然后求出其斜率，也就是tanθ，這樣三角代換思想自然形成，就可以從三角函數的角度進行解題.

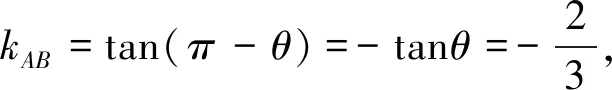
從而得出直線方程是2x+3y-12=0.

2.3 等量代換

在高中數學學習中，概率問題一直是一個難點，很多學生對概率問題理解不清楚，導致在解題過程中無法對題目進行有效轉化.實際中，概率問題涉及范圍比較廣，如果學生本身的理解能力比較差，并且不會對問題進行分析，那么就很難順利地解題.對此，教師可以引導學生在解題過程中采取等量代換的模式，在解題過程中對不影響最終結果的因素進行等量代換.

例3某工廠的某種產品成箱包裝，每箱200件，每一箱產品在交付用戶之前要對產品作檢驗，如檢驗出不合格品，則更換為合格品．檢驗時，先從這箱產品中任取20件作檢驗，再根據檢驗結果決定是否對余下的所有產品作檢驗，設每件產品為不合格品的概率都為p(0

(1)記20件產品中恰有2件不合格品的概率為f(p),求f(p)的最大值點p0.

(2)現對一箱產品檢驗了20件，結果恰有2件不合格品，以(1)中確定的p0作為p的值．已知每件產品的檢驗費用為2元，若有不合格品進入用戶手中，則工廠要對每件不合格品支付25元的賠償費用.

(i)若不對該箱余下的產品作檢驗，這一箱產品的檢驗費用與賠償費用的和記為X，求EX；

(ii)以檢驗費用與賠償費用和的期望值為決策依據，是否該對這箱余下的所有產品作檢驗？

令f′(p)=0，得p=0.1.當p∈(0,0.1)時，f′(p)>0；當p∈(0.1,1)時，f′(p)<0.

所以f(p)的最大值點為p0=0.1.

(2)由(1)知，p=0.1.

(i)令Y表示余下的180件產品中的不合格品件數，依題意知Y～B(180,0.1)，X=20×2+25Y，即X=40+25Y.

所以EX=E(40+25Y)=40+25EY=490.

(ii)如果對余下的產品作檢驗，則這一箱產品所需要的檢驗費為400元，由于EX>400，故應該對余下的產品作檢驗.

綜上所述，在高中數學解題中，通過代換法的應用，可以顯著提高學生的解題效率，引導學生對復雜的數學問題進行簡單化處理，這對于學生學習效果的提升有極大幫助.因此，在實踐教學中，高中數學教師必須引導學生樹立良好的代換意識，結合題目中的已知條件，合理地運用代換法進行解題，促進學生解題準確性的提升.