基于n階多項式改進退水曲線的枯水期徑流預測方法

董亞迪，廖勝利，燕志宇，張世欽

(1.大連理工大學水電與水信息研究所，遼寧大連116024；2.國網福建省電力有限公司，福建福州350003)

0 引 言

枯水期流域內降水及來水量都較少，水資源供需矛盾突出，無論是跨流域水量分配，還是水電調峰調度都要求水庫特別是調節性能較差(季調節及以下)的水庫有比較準確的日來水量預測；因此，開展枯水期徑流預測對充分發揮水庫效益及提高水電站發電調度水平具有重要意義[1-2]。枯水期徑流主要由汛末滯留在流域內的蓄水量消退以及枯水期降雨形成，影響因素非常復雜，主要包括以氣候和地質為主的自然因素及工農業用水等人為因素[3]，河流斷面徑流量呈逐漸消退趨勢但預測極為困難。

目前，枯水期徑流預測大多采用比較簡單的傳統方法，主要包括退水曲線法[4-5]、前后期徑流相關法[6]、回歸分析法[7]、人工神經網絡法[8]和遺傳算法[9]等，尤以退水曲線法應用最為普遍。趙銅鐵鋼等[10-11]采用隨機森林模型對長江上游屏山站和寸灘站枯水期徑流預報進行了探討，研究結果顯示，隨機森林模型能有效選取水文—氣象預報因子進行徑流預報。近年來，隨著氣候條件的改變以及人為因素的影響，流域特性和枯水期徑流規律有了一定的變化[12]，因此為了提高預測精度，需要對傳統退水曲線法做出改進。

本文針對退水曲線公式中消退系數隨時間逐漸遞增的關系，提出用n階多項式函數曲線擬合消退系數，構建了改進的退水曲線預測模型，通過比較各模型預測值平均偏差率選取最佳預測模型，并結合典型年法給出了枯水期徑流預測的具體步驟。最后將該模型應用于瀾滄江流域功果橋水電站枯水期徑流預測，預測效果良好，模型可供其他電站或流域參考和應用。

1 常規退水曲線

當忽略枯水期少量的降雨時，枯水期徑流的來源主要是汛末滯留于流域內的蓄水量，包括地下蓄水量和河網蓄水量。對于由地下水補給的河流，可以近似地認為地下蓄水量與出流量之間為線性關系，因此其蓄量方程可以表示為

-Qg(t)=dWg(t)/dt

(1)

Wg(t)=kgQg(t)

(2)

整理后可得

dGg(t)/Gg(t)=-(1/kg)dt

(3)

求解式(3)可得

Qg(t)=Qg(0)e-t/kg

(4)

式中，Wg(t)為t時刻的地下蓄水量，m3；Qg(t)為t時刻的出流量，m3/s；Qg(0)為退水開始時刻t=0時的出流量，m3/s；ks為常數。

同理，由河網蓄水量補給的枯水期徑流，其蓄泄關系也近似呈線性，則出流量Qr(t)的消退規律是

Qr(t)=Qr(0)e-t/kr

(5)

式中，Qr(t)為t時刻的出流量，m3/s；Qr(0)為退水開始時刻t=0時的出流量，m3/s；kr為常數。

一般情況下，流域的退水過程是地下蓄水量和河網蓄水量共同補給的結果，可用一個總的退水公式表示。即

Q(t)=Q(0)e-t/K

(6)

式中，Q(0)、Q(t)分別為退水開始時刻t=0時的流量和t時刻的流量，m3/s；K為常數，其定義為

W(t)=KQ(t)

(7)

式中，W(t)為t時刻的蓄水量，m3。

式(7)表明，當泄流流量恒定為Q(t)時，蓄水量W(t)泄完所需的時間正好為K。由于蓄水量分布在流域的各個位置上，距出口斷面的距離遠近不同，匯集時間大小不等，因此K可解釋為流域水流平均匯集時間。

若簡化式(6)為

(8)

則

Cg=e-1/K

(9)

式中，Cg為常數。由于K為流域水流平均匯集時間，則Cg也可反映退水速率的快慢，稱為消退系數。式(8)即為常規的退水曲線公式。因此，掌握了Cg的變化規律就掌握了退水曲線的規律，分析退水曲線就是分析Cg的變化。

2 改進退水曲線預測模型

2.1 常規方法存在的問題

傳統方法計算時，首先把退水曲線式(8)表達為遞推形式(Δt=1 d)

Q(t+1)=CgQ(t)

(10)

由式(10)知，消退系數Cg可直接由計算時段始末的兩個實測退水流量來確定。即

Cg=Q(t+1)/Q(t)

(11)

因此，將相鄰時段流量數據組成樣本系列，通過均值法或最小二乘法求出該流域的消退系數Cg。當用最小二乘法來估計消退系數時，表達式為

(12)

式中，n為樣本系列中相鄰時段流量數據組的組數，即一組樣本系列中有n組觀測值；括號中i為觀測值序號，第二個數字為前后時段序號。即，Q(i，1)為第i組觀測值的前一時段流量，Q(i，2)為第i組觀測值的后一時段流量。

雖然最小二乘法考慮了一次退水過程每個時段的流量數據，但是當把求得的Cg作為固定的常數代入式(8)進行枯水期徑流預測時，會發現預測值偏差較大，結果往往達不到較好的效果。其原因是，此方法將Cg簡化成了一個恒定常數；然而，當我們直接利用原流量系列Q(t)和Q(0)之間的函數關系反向推求Cg，不難發現Cg并非為一個恒定常數，而是隨時間t大致呈遞增趨勢。而且在最小二乘法中，Cg的推求是通過Q(t)和Q(t+1)的關系得到的；而在退水預測時，卻是運用初始時刻的退水量即Q(0)和Q(t)的關系，這樣難免會造成Cg求解方法上的矛盾及較大的誤差。

2.2 基于n階多項式的改進退水曲線

由于Cg并非是一個恒定常數，其隨時間t大致呈遞增的趨勢。根據其遞增的規律和線型，本文采用與傳統方法不同的假設，認為Cg是隨時間變化的n階多項式函數。即用多項式函數擬合Cg。根據枯水期徑流資料，利用Q(t)和Q(0)之間的函數關系推求Cg系列值后，用n階多項式函數曲線進行擬合，發現：當階數大于等于4時，擬合曲線會出現振蕩，引起過擬合情況；隨著多項式階數增加，曲線擬合偏差會越來越大，徑流預測值曲線和實際流量曲線的偏差也會越來越大。因此，本文用多項式函數擬合Cg時，只考慮一階、二階和三階三種情況。即

(13)

(14)

(15)

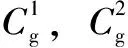
將擬合結果代入式(8)可得改進退水曲線公式(下式中的i式(12)已用，不能再表示另一個物理概念，需換符號j，以下相關均需改)

(16)

式中，j為階數，取1，2，3；Qi(t)為j階多項式對應的t時刻預測流量值。

故本文采用改進退水曲線式(16)進行枯水期徑流預測。關于改進退水曲線的最佳預測模型選擇標準，本文采用預測值偏差率式(17)來判斷。首先根據式(16)進行枯水期徑流預測，然后根據式(17)計算每個退水曲線公式預測值對應的平均偏差率，取平均偏差率最小值對應的退水曲線公式作為此次預測的最佳預測模型。即

(17)

2.3 典型年選擇方法

對于某個特定流域，枯水期徑流消退規律在歷年中往往表現出較好的重復性。基于n階多項式的改進退水曲線模型和常規退水曲線法一樣，仍然是一種利用歷年徑流變化規律來預測枯水期徑流的預測方法。因此，本文采用典型年法來獲取歷史徑流資料，作為枯水期徑流預測依據。

隨著人們生活方式的改變，人類活動的影響和氣候變化對流域枯水期徑流的影響不容忽視[11]。因此，在選擇典型年徑流資料時，這些影響因素需要考慮進來。由于近20年內流域特性和枯水期退水規律與預測年份相比往往更加相似；因此為了提高預測準確度，本文將典型年選擇范圍縮短至近20年歷史徑流資料內。

典型年流量資料選擇標準有兩個：第一，確定預測初始時刻退水流量，在歷史同期徑流系列中找出流量大小與預測年份較為相近的年份作為典型年候選年份(百分誤差不大于3%)。第二，計算預測初始時刻前10天平均流量，以及典型年候選年份中同期時段的平均流量，從而確定二者的百分誤差。然后將典型年候選年份中初始時刻流量百分誤差和前10天平均流量百分誤差相加，找出百分誤差和最小年份作為典型年。確定第二個選擇標準的原因是，流域預測初始時刻前期蓄水情況和徑流量對流域退水過程會有較大影響作用。

2.4 預測求解步驟

利用改進退水曲線模型進行枯水期徑流預測時，依據有兩個：預測年份初始時刻退水量Q(0)和利用典型年徑流資料擬合得到的Cg多項式函數。該公式并未考慮流域實際面臨的各種復雜氣候條件和人為因素。如果預測時段過長，突發性氣候和人類活動對退水過程的影響就會大大增加；因此預測誤差也會更大。長期的枯水期徑流預測準確性和可信程度都偏低，使得水庫實際調度時必須考慮來水情況的各種變化。因此，為了提高預測準確性，本文將一次預測周期確定為30 d。

本文利用改進退水曲線模型進行枯水期徑流預測的流程具體步驟如下：

(1)確定預測年份初始時間，根據典型年流量資料選擇標準確定典型年。

(2)根據典型年流量資料，確定消退系數Cg實際變化過程線，然后擬合得到Cg的一階、二階和三階多項式函數。

(3)將擬合到的Cg多項式表達式代入常規退水曲線式(8)，得到改進退水曲線公式。

(4)將預測年份起始流量Q(0)代入改進退水曲線式(16)，進行逐日流量預測。

(5)計算每個改進退水曲線公式預測值對應的平均偏差率，取平均偏差率最小值對應的退水曲線公式作為此次預測的最佳模型。最佳模型預測值即為最終預測成果。

3 實例研究

3.1 實例背景及資料

本文以瀾滄江流域為實例進行研究。瀾滄江在我國境內長2 130 km，落差約5 000 m，流域面積17.4萬km2，水能資源蘊藏量約3 656萬kW。全流域屬西南季風氣候，其顯著特點是干、濕兩季分明，一般5月至10月為濕季，11月至次年4月為枯水期，約85%以上降水量集中在濕季；而又以6月～8月為最集中，3個月降水量占全年降水量60%以上。枯水期降水量很小，枯水期徑流主要由流域前期蓄水補給，流量過程呈現較穩定的消退趨勢。

功果橋水電站是瀾滄江干流水電基地中下游河段“兩庫八級”梯級開發方案的龍頭電站。本文以功果橋水電站壩址斷面1996年～2015年中的20年日平均流量資料作為歷史徑流數據庫選擇典型年，進行枯水期徑流預測，并用2016年實際流量數據進行成果檢驗。

3.2 參數計算及選擇

以2016年11月11日為預測起始日期，起始流量為998.13 m3/s，前10天的平均流量為1 081.37 m3/s。根據典型年選擇標準在歷史數據中確定典型年為2013年。起始日流量為1 024.69 m3/s，誤差為2.5%，符合候選典型年選擇標準；前10天的平均流量為1 120.41 m3/s，誤差為3.4%，二者的誤差和為5.9%，在候選典型年系列中為最小值，符合典型年選擇標準。

根據典型年流量數據，對消退系數Cg進行多項式函數擬合，可得Cg的一階、二階和三階多項式

(18)

(19)

0.004t+0.926 2

(20)

將擬合到的Cg表達式代入常規退水曲線式(8)，即可得改進退水曲線公式。

3.3 計算結果及分析

圖1為典型年流量系列Cg曲線、多項式擬合曲線和最小二乘法Cg曲線。從圖1可以看出，典型年流量消退系數Cg隨時間t大致呈遞增的趨勢。當采用傳統的最小二乘法處理時，將典型年相鄰時段流量數據組成樣本系列，根據最小二乘法式(12)可求出該流域消退系數Cg=0.971；此時，退水曲線公式中的Cg被視為一個恒定的常數，處理后的結果是實際的Cg和預測公式中的Cg有較大偏差。二階和三階多項式函數擬合效果要好于一階多項式函數。相比較三階多項式函數、二階多項式函數的擬合效果稍有優勢。

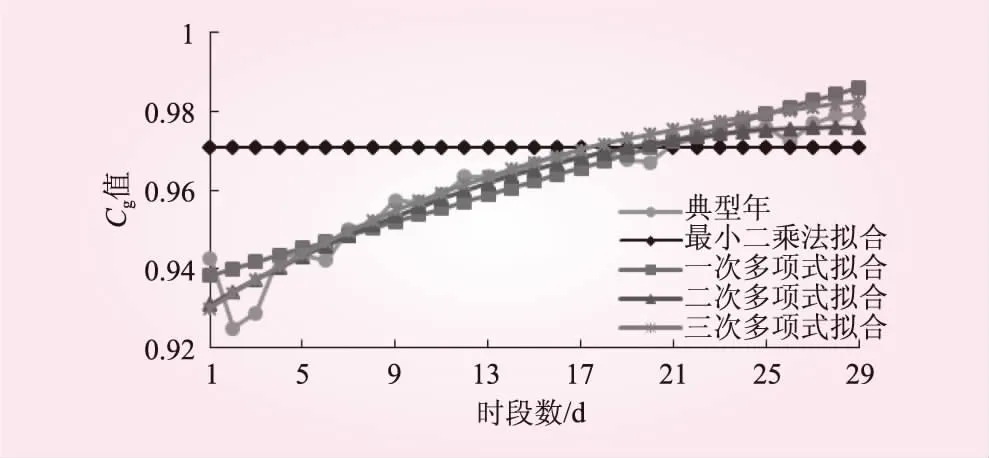
圖1 典型年Cg曲線和擬合曲線

將2016年11月11日流量Q(0)=998.13 m3/s代入改進退水曲線公式對11月12日至12月10日30天流量進行預測；同時，將Q(0)=998.13 m3/s和通過最小二乘法求出的Cg=0.971代入常規退水曲線式(8)進行預測，得到預測流量值(見圖2)。根據式(17)得不同預測方法下的平均偏差率：最小二乘法為10.85%；一階多項式為7.25%；二階多項式為2.84%；三階多項式為7.37%。

圖2 2016年實際流量曲線和預測流量曲線

從圖2的4條預測流量曲線可明顯看出，最小二乘法預測結果與實際流量的偏差最大，平均偏差率為10.85%；在前期大部分時間多項式函數預測結果和實際流量都非常接近，但尾部階段差異越來越大。與2016年實際流量數據行對比，二階多項式預測方法明顯優于一階多項式和三階多項式預測方法。因此，本次預測的最佳模型為基于二階多項式的改進退水曲線模型。

其中，11月29日和30日二階多項式預測流量與實際流量相比有些許的偏差。查看歷史降雨資料得知，原因是這段時間內瀾滄江流域內有一些局部降雨，從而引起實際流量略大于預測流量。整體來看，從11月中旬到12月中旬二階多項式的預測流量曲線與實際流量曲線基本吻合，平均偏差率僅為2.84%，預測效果良好。

4 結 語

本文分析了枯水期徑流預報的重要性，介紹了枯水期徑流的主要來源和影響因素。針對退水曲線公式中消退系數隨時間t逐漸遞增的關系，提出用n階多項式函數曲線擬合消退系數，從而構建了基于n階多項式的改進退水曲線預測模型，通過比較各模型預測值平均偏差率選取最佳預測模型，并結合典型年法給出了枯水期徑流測的具體步驟。

本文以瀾滄江流域功果橋水電站為實例，對2016年11月11日至12月10日進行了30天的枯水期逐日徑流預測，通過比較各模型預測值平均偏差率，確定最佳模型為基于二階多項式的改進退水曲線預測模型，其預測效果良好，可供其他電站或流域參考和應用。