基于穩定性演化路徑的反傾斜坡變形演化特征研究

謝良甫，張佳琪，譚順利，王 博

(新疆大學建筑工程學院，新疆烏魯木齊830046)

0 引 言

一般認為，反傾斜坡穩定性較好，不易產生貫通性的滑面，因而對其關注度遠不如順層斜坡。然而，隨著人類工程活動范圍的不斷擴大，此類邊坡的穩定性問題不斷凸顯，且發育規模巨大，嚴重威脅著工程建設[1]。大量工程案例表明，反傾巖質斜坡變形破壞的一個典型特征是其彎曲折斷面一般需經歷較長的孕育時間，而一旦失穩，其破壞規模是巨大的，破壞程度也通常是非常劇烈的，危害相當嚴重[2]。因此，研究反傾斜坡長期時效變形演化特征，對反傾斜坡的防災減災具有重要的理論意義。

目前，對反傾邊坡變形演化研究主要借助工程地質分析[3]、物理模型試驗法[4-7]以及數值模擬法[8-11]。張國新等[12]采用數值流形法進行了反傾斜坡傾倒變形破壞特征的模擬，并與離心機模型試驗結果進行了對比分析；任光明等[13]從河谷演化、成坡角度研究了反傾斜坡變形演化過程；羅勇和龔曉南[14]采用離散元UDEC軟件進行了節理發育的反傾斜坡的變形破壞分析。這些研究成果的應用一般需要較為豐富的工程經驗或較為完備的科研條件，多停留于理論層次，在實際生產項目中難以推廣應用。為此，本文依托具體工程實例，選用常用的極限平衡分析法[15-19]，通過穩定性的變化研究反傾斜坡的變形演化特征，研究成果更易于應用于實踐。

1 反傾斜坡穩定性系數計算方法的確定

反傾斜坡不同于一般滑坡，對其條分時必須依托現有的巖層結構面，因此各條塊的邊界為不規則四邊形，現行規范建議的傳遞系數法難以準確計算穩定性系數。為此，本文選用Sarma法計算反傾斜坡穩定性系數。

Sarma法是一種基于極限平衡法的邊坡穩定性系數計算方法，該方法既能夠滿足力的平衡，亦能滿足力矩的平衡。Sarma法假定的邊坡體破壞形式和力學模型見圖1。圖1中，E、X分別為單元條塊兩側在法向與切向的作用力；T為條塊底部切向作用力；U為條塊所受水壓力；N為條塊底部支撐反力；Wi為條塊自重；KcWi為Sarma法構建的一個體積力；Fi為條塊所受外力。

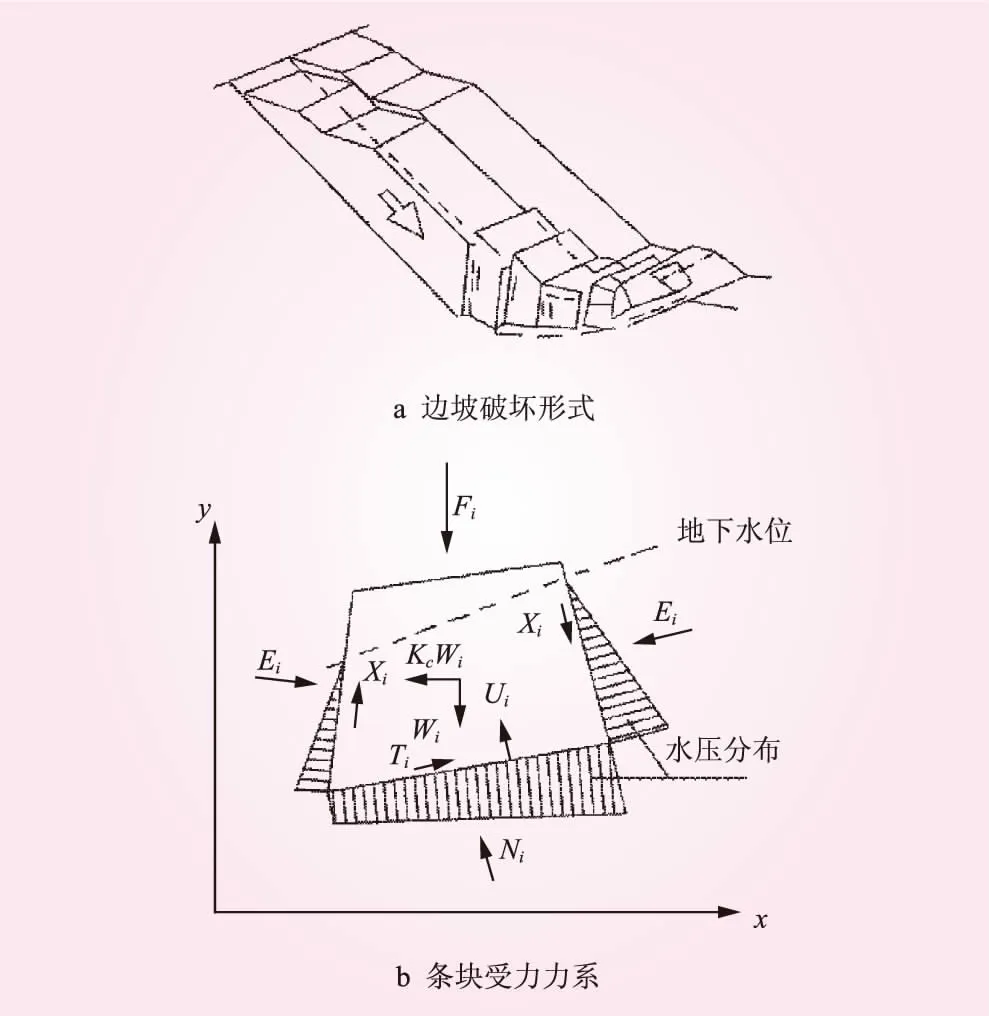
圖1 Sarma法

根據條塊受力分析，體積力KcWi中的Kc是邊坡臨界加速度系數，即ηb。假定滑坡體在該力的作用下處于極限平衡狀態，分別對條塊水平和鉛垂線方向建立力的平衡方程得

Nicosαi+Ticosαi=Wi+Xi+1cosδi+1-Xisinδi-

Ei+1sini+1+Eisinδi

(1)

Ticosαi-Nisinαi=KcWi+Xi+1sinδi+1-Xisinδi+

Ei+1cosδi+1-Eicosδi

(2)

式中，αi為條塊底面與水平方向的夾角；δi為條塊左側邊界與鉛垂線方向夾角。

根據摩爾-庫侖破壞判據，分別對條塊底部、左側、右側進行受力分析，有

Ti=(Ni-Ui)tanφi+ci+bisecαi

(3)

(4)

(5)

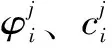
Ei+1=ai-piηb+Eiei

(6)

由于式(6)是迭代循環式，故

En+1=an-pnKc+Enen

(7)

En+1=(an+an-1en)-(pn+pn-1en)Kc+En-1enen-1

(8)

進一步迭代得

En+1=(an+an-1en+an-2enen-1+…)-Kc(pn+pn-1en+pn-2enen-1+…)+E1en-1en-2…e1

(9)

在無外荷載作用時，En+1=E1=0，故KC可表達為

Kc=(an+an-1en+an-2enen-1+…+a1enen-1…e3e2)/

(pn+pn-1en+pn-2enen-1+…+p1enen-1…e3e2)

(10)

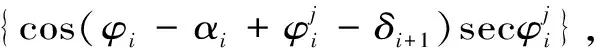
Sarma法在斜坡穩定性系數計算過程中引入了邊坡臨界加速度系數Kc，在無地震動荷載作用下，可類似于強度折減法通過同時折減滑面、滑體的抗剪強度值，直至Kc趨于0，此時的折減系數即為斜坡穩定性系數。

根據Sarma法計算原理，本文采用Matlab結合CAD編制Sarma法穩定性系數計算程序，通過CAD提取各條塊角點坐標和地下水位線坐標，并將坐標信息導入Matlab中，計算不同折減系數F所對應的Kc值。最后，通過Matlab中的CFtool工具進行數據擬合，取Kc=0所對應的折減值F，即斜坡的穩定性系數，見圖2。

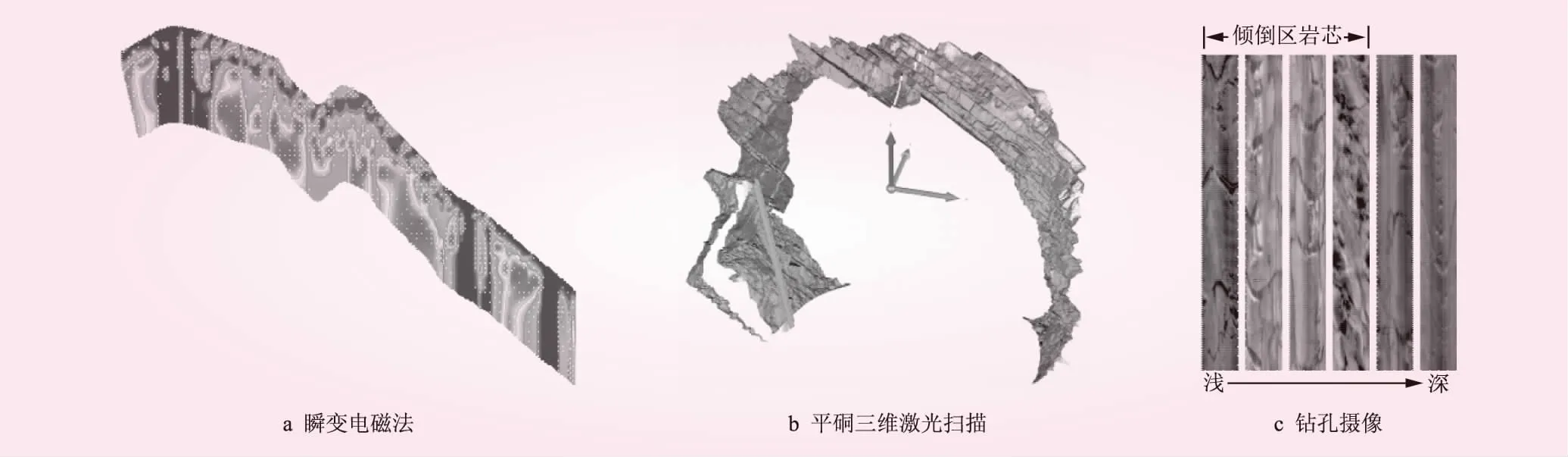
圖4 勘察成果

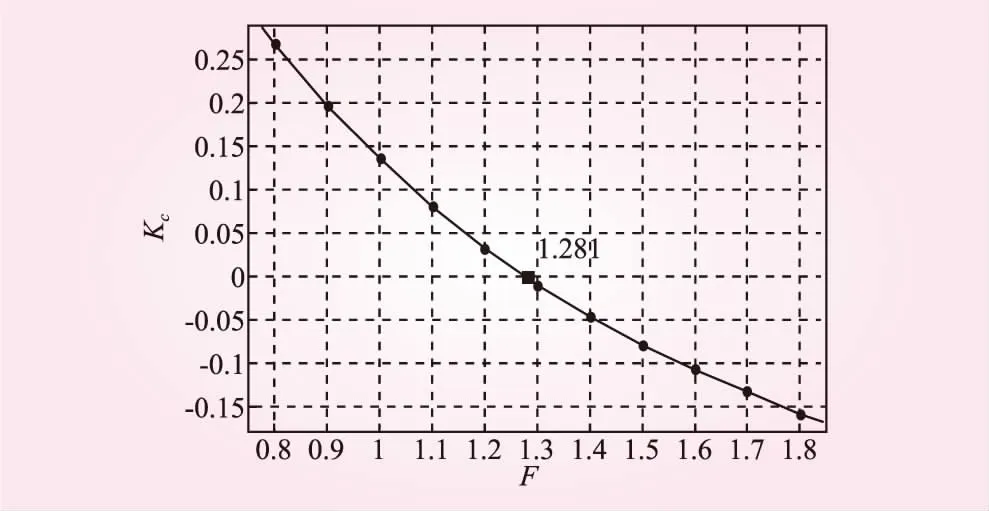
圖2 穩定性系數

2 計算模型

2.1 工程概況

中梁水庫斜坡位于重慶巫溪縣中梁水庫上游約1.2 km右岸，斜坡坡腳高程526 m、坡頂高程1 183 m，坡體寬約700 m，坡面溝谷發育，斜坡中前部坡度較陡，后部相對較緩。自水庫蓄水后，斜坡體不同部位出現了較為明顯的變形破壞現象。

根據現場地質調查，中梁水庫斜坡為一典型反傾斜坡，斜坡體局部已發育形成一定規模的傾倒折斷面，目前折斷面尚未貫通，處于變形發展階段，急需對其變形演化方向做出準確判斷。中梁水庫反傾斜坡變形特征見圖3。

圖3 反傾斜坡變形特征

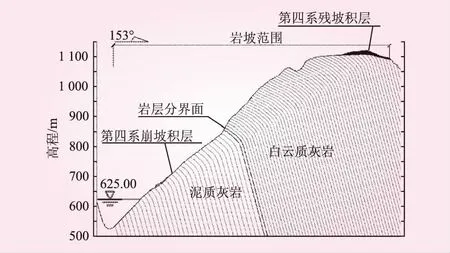
圖5 反傾斜坡穩定性評價模型

2.2 模型建立及參數選取

在地表地質調查基礎上，分別通過瞬變電磁法、平硐三維激光掃描、鉆孔攝像等勘察成果(見圖4)，獲取反傾斜坡傾倒變形范圍及巖層傾角隨深度變化規律。選取斜坡典型縱斷面(見圖5)，構建斜坡穩定性評價模型。

通過現場原位直剪試驗并結合室內巖石試驗，獲取中梁水庫斜坡巖土體物理力學參數。巖體物理力學參數見表1。結構面力學參數見表2。

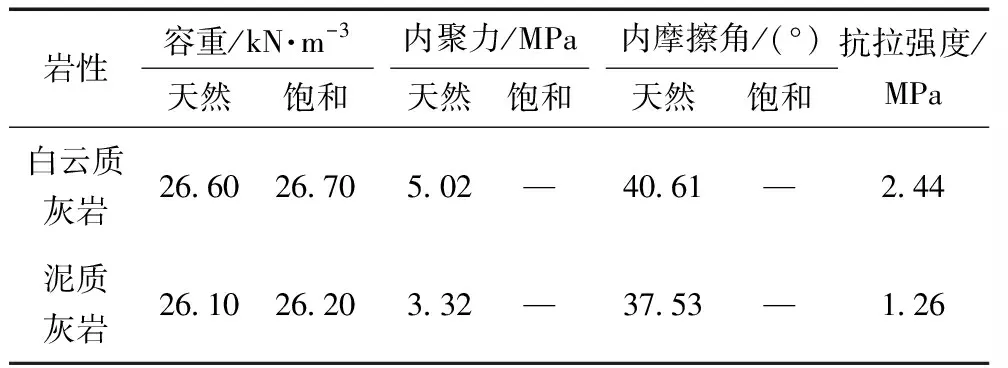
表1 巖體物理力學參數

表2 結構面力學參數

3 反傾斜坡傾倒變形分析

3.1 演化規律

反傾斜坡傾倒變形演化過程實質是穩定性降低的過程，通過分析傾倒變形穩定性演化路徑能在一定程度上表征傾倒變形的演化過程。根據Goodman-Bary理論，反傾斜坡發生變形的巖層條塊分為下部滑移區、中部傾倒區和上部穩定區(見圖6)，圖6中，ΔL為條塊寬度；k為節理連通率；b為臺階高度。在傾倒變形演化過程中，穩定區條塊將逐級發生傾倒成為傾倒塊體，而傾倒塊體傾角將進一步增大，從而提供了更大的下滑力，進而推動滑移區，使斜坡發生整體破壞。本文采用變化巖層傾倒傾角與傾倒條塊數2個變量分析反傾斜坡整體穩定性系數的變化規律。

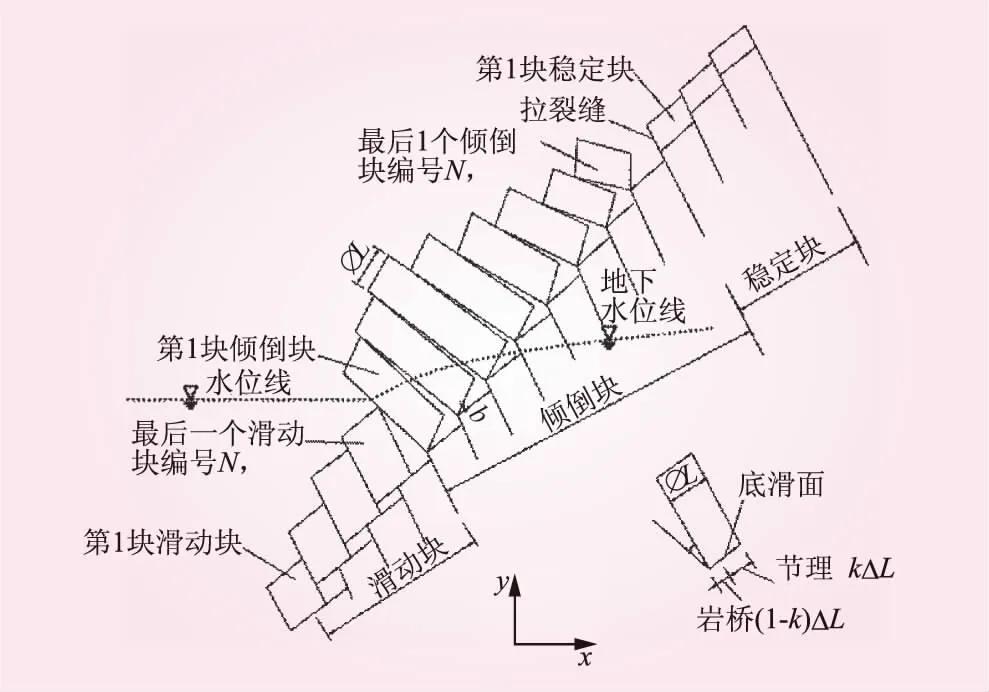
圖6 反傾斜坡穩定性評價模型

無外因作用下，反傾斜坡將在自重作用下其坡體一定范圍內巖層塊體發生一定程度的傾倒變形。因此，在上述反傾斜坡穩定性計算程序中，通過遍歷不同的傾倒條塊數和傾倒角度即可得出不同組合下反傾斜坡穩定性系數，采用插值法即可得出穩定性系數云圖，見圖7。

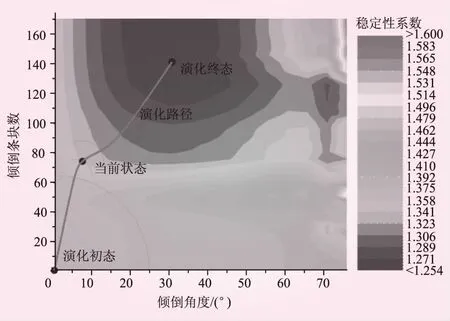
圖7 斜坡傾倒變形演化路徑

從圖7可知，不同傾倒條塊數和傾倒角度的組合下，斜坡穩定性系數主要變化范圍在1.26～1.50間。傾倒條塊數為120～175塊、傾倒角度為20°～40°時，斜坡穩定性系數最低。斜坡傾倒變形演化初期狀態為傾倒條塊數為0、傾倒角度為0，即坐標原點，從系統演化的角度分析，反傾斜坡會沿坐標原點沿穩定性系數降低最快、最短的路徑進入穩定性最低的區域。因此，以坐標原點為初始點，按穩定性系數降低最短路徑，即可得出系統演化路徑。采用Goodman-Bary法分析當前斜坡變形狀態時，傾倒條塊和穩定條塊的分界點位于第76個條塊，得出斜坡當前傾倒條塊已發生約8°的偏轉傾角。此時，斜坡穩定性系數已演化至路徑拐點處，斜坡前期變形主要以傾倒條塊數增加為主，后續演化將表現為傾倒條塊數和傾倒角度同步快速增加，表明變形在加劇，穩定性加速降低。

3.2 演化路徑

實際中，反傾斜坡不可避免受到外因作用而加劇其變形演化。其中，地下水是誘發邊坡失穩的一個最常見也是影響較為顯著的因素。因此，本文以庫水作用為例，分析外因對反傾斜坡穩定性演化路徑的影響。

受大壩調度庫水位會發生變化，由于Sarma法中沒有考慮水的動水壓力，故本文將庫水位視為不變簡化計算。在上述研究基礎上，從當前斜坡演化階段開始加入庫水作用，分析庫水作用加入前后反傾斜坡穩定性演化路徑的變化情況。庫水作用下斜坡傾倒變形演化路徑見圖8。

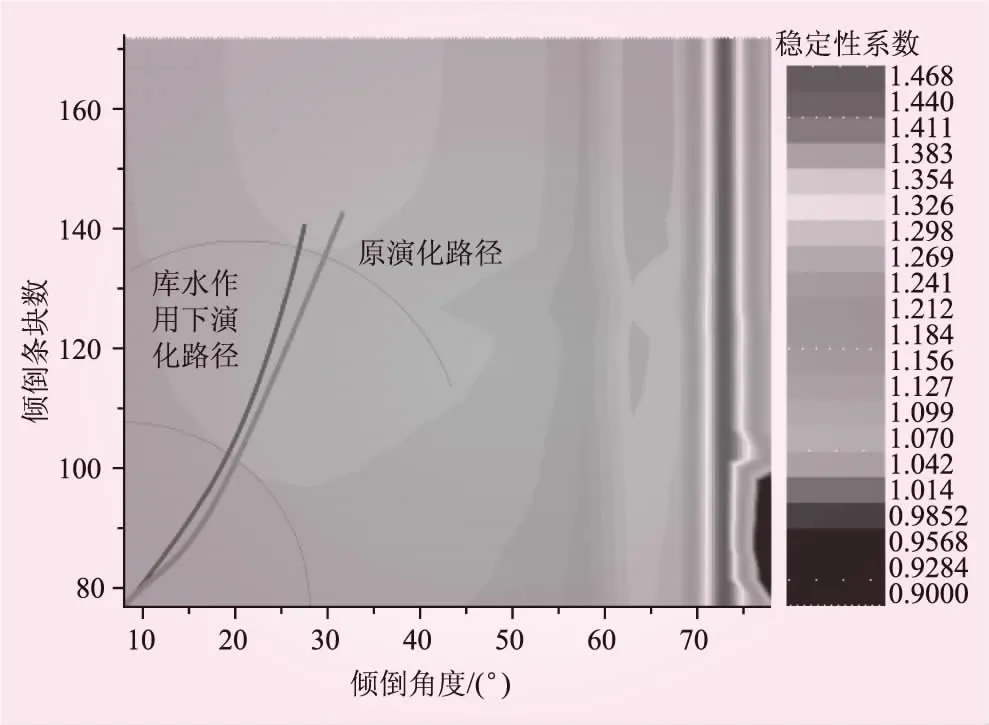
圖8 庫水作用下斜坡傾倒變形演化路徑

從圖8可知，庫水作用加入后，斜坡穩定性演化路徑發生輕微偏移，無顯著差異，但斜坡的穩定性降低較明顯，平均降低約0.2左右。因此可以推斷，庫水因素只是降低了反傾斜坡各階段的穩定性，但對其演化路徑影響較小，即只是加速了反傾斜坡的變形。

4 結 語

本文在現場地質調查與各種勘測技術成果的基礎上，獲取了反傾斜坡穩定性評價剖面，利用Sarma法計算反傾斜坡傾倒變形穩定性系數，并通過穩定性演化路徑研究了傾倒變形演化特征，得出以下結論：

(1)反傾斜坡傾倒變形穩定性演化路徑拐點位于傾倒條塊數80塊(約斜坡整體條塊數的一半)、傾倒角度8°附近，拐點前后反傾斜坡變形特征差異較明顯。

(2)反傾斜坡傾倒變形前期變形方式表現為以傾倒條塊數增加為主，條塊傾倒傾角增加較緩慢，因此宏觀上傾倒變形特征不夠明顯；進入拐點后，其變形將發生較明顯轉變，表現為傾倒條塊數和傾倒角度同步快速增加，宏觀上呈現典型的傾倒變形特征。

(3)庫水等外因對反傾斜坡穩定性降低較明顯，但對穩定性演化路徑的改變較小，表明庫水等外因只是加劇了反傾斜坡的變形速率，對其演化方向影響較小。