基于數學核心素養的初中教學探究
——以同題異構課“平行四邊形復習課”為例

■許凌燕

一、課例探究

1.立足學情，把握起點。

學生原有的知識和經驗是教學活動的起點。任何有效的教學都始于對學生已有經驗的充分挖掘和利用，這種經驗包括認知經驗和生活經驗。

此次上課的兩位教師來自不同學校，屬于借班上課，因此了解學情就顯得尤為重要。事實上，在兩位教師得知在該校上課以后，就已經與對應班級任課教師以及班主任溝通，了解了學生的整體情況，對特殊的個體情況也有了初步的了解。在上課前一天，教師A還到對應班級與學生見面，分發學案，布置預習，相互交流。特級教師任小文曾說，我每次出去上公開課，一定會提前到班級和學生溝通幾句，師生的相互了解、情感的建立是完成目標的基石。

兩位教師通過精準定位學情，充分調動學生參與課堂的主動性、積極性。筆者認為正是因為備課時能從學情出發，充分考慮到學生的最近發展區，才能將數學核心素養的培養融入到整個課堂之中。

2.創設情境，梳理知識。

情境應成為學生的思維發生處、知識形成處、能力成長處、情感涵育處，創設情境就是構建課程知識內容并使之與學生的生活、經驗、情感、生命相接的過程。好的情境引入能激發學生的感性思維和探究世界萬物的渴望和能力。兩位教師在階段性復習課中也能注重創設情境，激發學生思維。

教師A的引入：

（1）如圖1，已知四邊形ABCD的周長為24cm，其中AB∥DC，AD∥BC，且AB=5cm，則BC=_______cm，AD=_______cm，CD= cm。

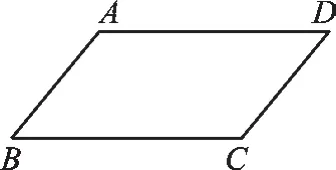
圖1

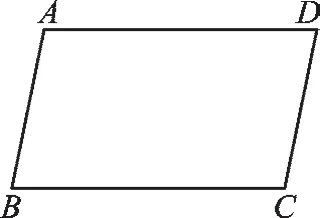
圖2

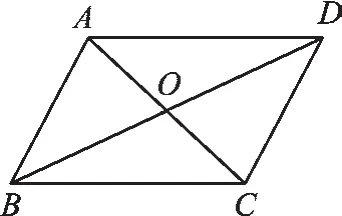
圖3

（2）如圖2，在 ?ABCD 中，∠A+∠C=200°，則∠A=______°，∠D=______°。

（3）如圖3，已知?ABCD 中，AC=10cm，BD=16cm，則BC的取值范圍是______。

（4）在四邊形ABCD中：若AB∥CD，要使四邊形ABCD是平行四邊形，則需添加的條件是_____；若AD=BC，要使四邊形ABCD是平行四邊形，則需添加的條件是______。

教師B的引入：

如圖4，你能以AB、BC為一組鄰邊，還原?ABCD嗎？

圖4

兩位教師的情境引入各具特點。教師A以題帶知識點，激發學生回顧已有知識，構建框架結構，厘清知識脈絡；教師B的引入以一個開放性的生活問題入手，讓學生結合“平行四邊形的判斷”梳理出問題的結果，運用性強。兩種不同風格的設計促使學生的認知從感性認識上升為理性認識，同時，也促進了學生形象思維和抽象思維相互轉化。

3.自主探究，合作提升。

建構主義認為，學生的學習并不是一個被動接受的過程，應該在已有知識經驗的基礎上建構新知識，實現知識的再創造。蕭伯納曾說：“你有一個蘋果，我有一個蘋果，彼此交換一下，我們仍然是各有一個蘋果；但你有一種思想，我有一種思想，彼此交換，我們就都有了兩種思想，甚至更多。”《義務教育數學課程標準》明確要求教師引導學生獨立思考，自主探索，合作交流。自主強調的是個人的主動性、積極性，渴望獲得知識的一種心理特質。合作交流是自主探究的升華，是思想和智慧碰撞的途徑。

教師A的探究性問題：

如圖 5，在矩形 ABCD 中，AB=a cm，AD=10cm，點P在邊AD上以每秒1cm的速度從點A向點D運動，點Q在BC邊上，以每秒4cm的速度從點C出發，由點C運動到點B，然后立即返回向點C運動。兩個點同時出發，當點Q到達點C時停止（同時點P也停止)。設運動的時間為t秒（t＞0）：（1）當t=______秒時，點Q與點C重合；（2）當點Q與點C重合時，點P運動的路程為cm；（3）在整個運動的過程中，t為何值時，四邊形PDQB是平行四邊形？

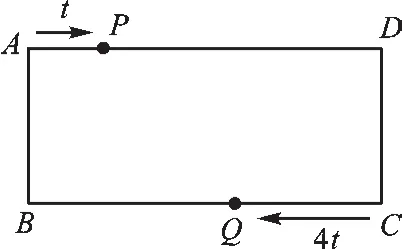
圖5

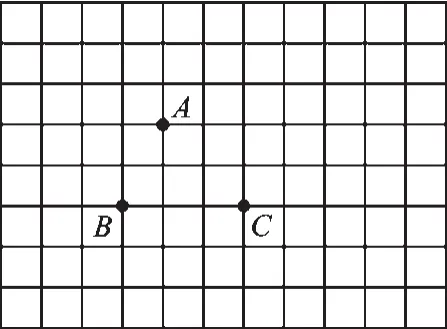
圖6

教師B的探究性問題：

如圖6，在邊長為1的正方形網格中有A、B、C三點,請你畫出以A、B、C為其中三個頂點的平行四邊形。（追問：請合理建坐標系，求出頂點坐標。）

兩位教師在課堂設計中都有意識地設計了探究環節。探究性問題的設計很有講究，假如難度太大，超出學生現有知識水平，學生則無法完成探究性問題，素養的培養成為空談；如果難度較低，在學生現有認知范疇內，探究性問題設計無效，學生沒有產生智慧碰撞的火花，數學推理、數學建模能力得不到提升。上述兩題型都涉及數學的分類討論思想。教師A先展示了學生自主探究的結果，針對學生考慮不全面的情況，再要求學生合作交流，完善推理過程，同時，教師A在各個小組之間進行指導。教師B先讓學生自主探究，而后小組交流展示。小組能呈現出完整分類的結果，但是在總結提煉上還欠“火候”。教師B最后給出解決此類問題的策略。

由此可見，合作交流不僅存在于學生之間，而且存在于組與組之間、師生之間。兩位教師為學生營造了一個探究的場所，引導學生形成了對“平行四邊形判定”的知識的“生長”。這是一種有效的“生長”，有潛力的“拔節”。

4.創新總結，提高認識。

教師在總結基礎知識、基本方法、數學思想的基礎上，對所學知識的必要性的闡述、研究的角度和經驗的總結也是極為重要的。一個精彩的總結有益于培養學生的邏輯思維、概括能力。

教師A從基本知識點、基本圖形、基本思想方法三個層面對本節課作了課堂小結；教師B從知識、思想、方法三個層面讓學生做了總結（如圖7）。數學教學的總結，除了總結認知層面基礎知識、基本能力和基本思想方法，還應該滲透非認知層面的情感和態度，滲透一種數學情感的培養，達到“一種意識，貫穿始終”。

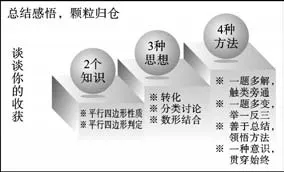
圖7

二、基于數學核心素養的幾點教學思考

1.從知識教學到素養教學，轉變教學思想。

通過兩節同題異構課的聽、評、悟，筆者的感觸是數學核心素養并非遙不可及的空洞理論，而是有具體可操作路徑的。這需要教師轉變教學觀念，從以怎么教為核心，向以學生怎么學為中心轉變，通過設計合理問題情境、實踐活動等，引導學生自主探究。課堂也不再是數學訓練的場所，而是引導學生“生長”的“萌發地”，讓數學核心素養培養真正落地，落實到具體的數學教學過程中。

2.以數學知識本質、學生認知為起點，設計教學內容。

在初中階段，學生認知的特點是思維的抽象邏輯性占主要優勢，但還屬于經驗型邏輯思維階段，在一定程度上需要感性經驗的直接支持。作為一線教師，應以學生的認知水平為出發點，關注學生學習的現實起點和邏輯起點，為學生后續的數學學習提供可持續的發展空間。

例如，目前初中教學中仍有教師將一元二次方程“韋達定理”補充到教學過程中，而蘇科版教材已經沒有此項內容。教師往往就是將公式交代給學生，然后配以適當練習。從學生層面上來說，這已經違背其認知規律；從數學知識本質上來說，“韋達定理”并不僅僅是一元二次方程根與系數的關系，這是法國數學家韋達提出的一元n次方程根與系數的關系，其中一元二次方程僅僅是其中的一種形式而已。這種違背學生認知規律的教學使得學生“一葉障目”，產生了誤區。所以，教師應加強數學知識的學習，認識數學知識的本質，這樣，在教學過程中，才能更大范圍地提供各種思維方式，給學生足夠的思維與想象的空間，為學生更好地理解數學知識的廣度與本質創設條件。

3.以有效任務為實施途徑，創設問題、探究活動。

布魯納曾說，有效教學始于準確地知道需要達到的教學目標是什么。明確的教學目標的實現需要通過有效的活動為途徑去落實，具體來說就是教師在進行教學問題、教學活動設計時，要充分考慮通過本節課的教學，可以培養或提升學生的哪些數學核心素養，這些素養可以通過哪些有效任務得以落實。例如，合理化的教學情境可以讓學生體會到數學來源于生活又服務于生活，培養學生的應用意識和數學建模能力；有梯度的、有廣度的、逐級深入的數學問題啟發學生思考，提升學生發現問題、提出問題、解決問題的能力和邏輯推理能力；合作化的數學活動培養學生的合作意識、團隊意識，使得學生在活動過程中，思維得以碰撞，使得學生與教師交流，學生之間相互交流，讓學生在思考和交流中，在掌握知識技能的同時，理解知識的本質，在顯性的活動中發展數學核心素養。