發(fā)展學(xué)生數(shù)學(xué)抽象能力的教學(xué)策略
■許禮光
數(shù)學(xué)抽象能力是舍去現(xiàn)實(shí)世界中事物的一切物理屬性,得到數(shù)學(xué)研究對(duì)象的能力。數(shù)學(xué)抽象包括:從數(shù)量與數(shù)量關(guān)系、圖形與圖形關(guān)系中,抽象出數(shù)學(xué)概念以及概念間的關(guān)系,從事物的具體背景中抽象出一般規(guī)律和結(jié)構(gòu),并且用數(shù)學(xué)符號(hào)或者數(shù)學(xué)術(shù)語(yǔ)予以表征。
數(shù)學(xué)抽象是學(xué)生形成理性思維的基礎(chǔ),它是數(shù)學(xué)本質(zhì)特征的反映,使得數(shù)學(xué)成為高度概括、準(zhǔn)確表達(dá)、結(jié)論可一般化的系統(tǒng)。在抽象能力形成的過(guò)程中,可以使學(xué)生加深對(duì)數(shù)學(xué)概念、命題、方法和體系的理解,可以使學(xué)生有效地理解和掌握數(shù)學(xué)的本質(zhì),可以更好地促進(jìn)學(xué)生養(yǎng)成運(yùn)用數(shù)學(xué)抽象思考并解決問(wèn)題的習(xí)慣,積累數(shù)學(xué)抽象的經(jīng)驗(yàn)。
一、基于現(xiàn)實(shí)發(fā)展抽象
史寧中教授認(rèn)為:數(shù)學(xué)抽象是從許多事物中舍去個(gè)別的、非本質(zhì)屬性,得到共同的、本質(zhì)屬性的思維過(guò)程,是形成概念的必要手段。這種基于現(xiàn)實(shí)的抽象,是從感性具體上升到理性具體的思維過(guò)程。
例如,“溫度計(jì)”是家庭必備工具,學(xué)生非常熟悉。“溫度計(jì)”以“零度”為界,零上與零下的“氣溫”從小到大排列,為此我們可設(shè)想:將“溫度計(jì)”看作“直線”,這個(gè)直線具有如下數(shù)學(xué)特征:有原點(diǎn),有統(tǒng)一的單位長(zhǎng)度、有數(shù)的增大方向,這樣就可將這個(gè)“溫度計(jì)”看成“數(shù)軸”了,可以得到數(shù)軸上的點(diǎn)可表示正數(shù)、0、負(fù)數(shù)。借助生活中冷暖體驗(yàn)的經(jīng)驗(yàn),從而可聯(lián)系到“數(shù)的大小比較”,得到比較有理數(shù)大小的“數(shù)軸”規(guī)則。
“有理數(shù)的加法法則”是學(xué)生進(jìn)入初中學(xué)習(xí)的第一個(gè)運(yùn)算法則,我們可以借助現(xiàn)實(shí)情境,設(shè)計(jì)系列問(wèn)題,讓學(xué)生感受引入負(fù)數(shù)后有理數(shù)是如何進(jìn)行加法運(yùn)算的。
我們首先作出這樣的規(guī)定:在足球比賽中贏球?yàn)椤罢保斍驗(yàn)椤柏?fù)”,這樣主場(chǎng)與客場(chǎng)兩場(chǎng)比賽的結(jié)果可用數(shù)學(xué)式子表示出來(lái)。例如,主場(chǎng)比賽贏2個(gè)球,客場(chǎng)比賽輸1個(gè)球,那么這一輪比賽結(jié)果為凈勝1個(gè)球。根據(jù)學(xué)生已有的經(jīng)驗(yàn),上述結(jié)果可這樣表示:(+2)+(-1)=+1。接著提出下列問(wèn)題供學(xué)生思考:
1.依照上面的表示,請(qǐng)說(shuō)出每輪比賽出現(xiàn)的不同結(jié)果情形,并用數(shù)學(xué)式子表示;
2.通過(guò)對(duì)所列算式的觀察,嘗試歸納出兩個(gè)有理數(shù)相加的所有情形,并總結(jié)有理數(shù)的加法法則;
3.“互為相反數(shù)的兩數(shù)和為零”與“法則中異號(hào)兩數(shù)相加的情形”有何聯(lián)系?
4.兩個(gè)有理數(shù)相加與小學(xué)學(xué)過(guò)的兩個(gè)數(shù)相加有何聯(lián)系與區(qū)別?
這里的設(shè)計(jì),既關(guān)注學(xué)生對(duì)有理數(shù)加法運(yùn)算法則的理解,又讓學(xué)生深刻體會(huì)到“負(fù)數(shù)”的意義和作用。
二、重視抽象過(guò)程設(shè)計(jì)
數(shù)學(xué)抽象是數(shù)學(xué)的基本思想。在數(shù)學(xué)抽象過(guò)程中,通過(guò)對(duì)一類問(wèn)題情境的觀察,發(fā)現(xiàn)研究對(duì)象的“屬性”;通過(guò)對(duì)“屬性”的分析,找出簡(jiǎn)約化的本質(zhì)特征,并高度概括;用數(shù)學(xué)的語(yǔ)言表示出“屬性”,使其適合具有“屬性”的所有對(duì)象;再通過(guò)建立聯(lián)系,納入學(xué)生原有的認(rèn)知系統(tǒng)。數(shù)學(xué)抽象活動(dòng)的順利進(jìn)行,關(guān)鍵在于設(shè)計(jì)合理的問(wèn)題與任務(wù),讓學(xué)生在概念、命題、方法和體系的形成過(guò)程中,經(jīng)歷數(shù)學(xué)抽象的過(guò)程,這是在知識(shí)形成過(guò)程中有效積累活動(dòng)經(jīng)驗(yàn)的基本策略。
“估算”是數(shù)學(xué)與生活聯(lián)系極為緊密的應(yīng)用,因?yàn)樯钪薪?jīng)常遇到的是估算而不是精確計(jì)算。“估算”涉及理解數(shù)的大小、修正調(diào)整數(shù)字等能力,這些能力均包含在數(shù)學(xué)抽象的基本特征中。由于估算一般都源自實(shí)際問(wèn)題,因此,我們需關(guān)注設(shè)置的情境要有現(xiàn)實(shí)意義。
例如,我們可以通過(guò)對(duì)學(xué)生熟悉的A4紙的長(zhǎng)與寬的估計(jì)、度量、折疊等活動(dòng),感受數(shù)(長(zhǎng)度)的大小(長(zhǎng)短)及倍數(shù)關(guān)系,同時(shí)感受無(wú)理數(shù)就在身邊。可設(shè)計(jì)如下的活動(dòng):
活動(dòng)1:觀察一張A4紙的兩個(gè)邊長(zhǎng),估計(jì)A4紙的長(zhǎng)與寬之比;
活動(dòng)2:度量A4紙的長(zhǎng)與寬,求出它們的比值,并與你的估計(jì)值進(jìn)行比較;
活動(dòng)3:將A4紙按下列圖示的方式折疊,說(shuō)出你的發(fā)現(xiàn);
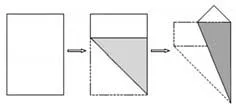
活動(dòng)4:將A4紙對(duì)折,取其一半,求其長(zhǎng)與寬的比并與A4紙的長(zhǎng)與寬的比進(jìn)行比較,說(shuō)出你得到的結(jié)論。
在上述操作的過(guò)程中,首先通過(guò)觀察,估計(jì)A4紙的長(zhǎng)與寬的大小關(guān)系;接著通過(guò)度量獲得長(zhǎng)、寬比的近似值;然后通過(guò)折疊,得出“折出的正方形對(duì)角線與A4紙的長(zhǎng)邊重合”,獲得A4紙的長(zhǎng)、寬的比為 2∶1。有了這樣的經(jīng)驗(yàn)后,再將A4紙對(duì)折“取其一半”,通過(guò)觀察及之前的折疊方式,發(fā)現(xiàn)仍然與A4紙有同樣的性質(zhì),再通過(guò)A4紙的長(zhǎng)寬之比計(jì)算半張紙的長(zhǎng)寬比,進(jìn)行理性的思考和證實(shí)發(fā)現(xiàn)的結(jié)論,這樣的再操作利于學(xué)生積累抽象活動(dòng)的經(jīng)驗(yàn)。
類似地,在研究三角形時(shí),我們一般遵循“定義、性質(zhì)、判定”的思路,通過(guò)“合情發(fā)現(xiàn)性質(zhì),猜想性質(zhì)逆命題的正確性并演繹證明”的方法,研究三角形邊的關(guān)系、角的關(guān)系,以及外角、中線、角平分線、高線的各自關(guān)系。上述三角形的研究經(jīng)驗(yàn)可以上升為一般幾何圖形的研究經(jīng)驗(yàn),我們可將這個(gè)方法遷移到四邊形研究中,這樣學(xué)生就會(huì)自然地提出四邊形到平行四邊形的研究問(wèn)題,自己規(guī)劃研究方案并實(shí)施。通過(guò)這樣的方法學(xué)習(xí)了平行四邊形的知識(shí)系統(tǒng),這種經(jīng)驗(yàn)可以引領(lǐng)學(xué)生繼續(xù)構(gòu)建矩形、菱形、正方形的知識(shí)系統(tǒng),并最終形成“平行四邊形——特殊的平行四邊形”的知識(shí)結(jié)構(gòu)系統(tǒng),完成平行四邊形相關(guān)知識(shí)的系統(tǒng)抽象。
三、合理采取抽象方法
數(shù)學(xué)抽象首先是發(fā)現(xiàn)屬性,其次是特征概括,接著是數(shù)學(xué)表示。“發(fā)現(xiàn)屬性”要求學(xué)生通過(guò)觀察、類比、聯(lián)想和結(jié)構(gòu)分析,從中找出“屬性”,并建構(gòu)出符合“屬性”的模型;“特征概括”要求學(xué)生能把模型一般化,通過(guò)類比、歸納和聯(lián)想找出一般化后的對(duì)象具備的共同特征,可以用式子、圖形、表格、程序等表示;“數(shù)學(xué)表示”要求學(xué)生表達(dá)準(zhǔn)確、簡(jiǎn)約。
例如,在分式概念教學(xué)時(shí),先出示一組具體生活背景的實(shí)例。
如果某市綠地面積為520萬(wàn)㎡,人口總數(shù)為30萬(wàn)人,那么該市人均擁有綠地㎡。
如果某市綠地面積為a萬(wàn)㎡,人口總數(shù)為b萬(wàn)人,那么該市人均擁有綠地㎡。
我們發(fā)現(xiàn),如果其中的數(shù)量?jī)H是小學(xué)學(xué)過(guò)的兩個(gè)整數(shù),那么其和、差、積都是整數(shù),而商不一定是整數(shù);如果其中的數(shù)量是兩個(gè)字母(或一個(gè)字母與一個(gè)整數(shù)),那么其和、差、積都是整式,而商不是整式,這個(gè)“商”的分子、分母都是“整式”,這有點(diǎn)像分?jǐn)?shù)的“除法運(yùn)算”,用類似分?jǐn)?shù)的式子將這個(gè)“商”表示出來(lái),如式子;接著,讓學(xué)生用類似的方法表示現(xiàn)實(shí)世界中其他一些關(guān)于兩個(gè)整式相除但結(jié)果不是整式的數(shù)量關(guān)系,得到若干個(gè)式子。
如果兩塊面積為m公頃、n公頃的棉田分別產(chǎn)棉花a kg、b kg,那么這兩塊棉田平均每公頃產(chǎn)
在“分式”的學(xué)習(xí)中,有分式概念的抽象,分式基本性質(zhì)的抽象,通分與約分方法的抽象,分式的運(yùn)算法則的抽象等。其中包含了概念的抽象、規(guī)則的抽象、方法的抽象,也包括建立分式知識(shí)系統(tǒng)的結(jié)構(gòu)抽象。因此我們?cè)诮虒W(xué)時(shí),要以某一種抽象方法為主線,將相關(guān)抽象方法整合在一起,使各種數(shù)學(xué)抽象活動(dòng)有序開(kāi)展。如分式的起始教學(xué)時(shí),我們可以系統(tǒng)結(jié)構(gòu)抽象為線索,以分式概念抽象為重點(diǎn),把分式概念抽象整合到系統(tǒng)結(jié)構(gòu)抽象的主線中。因此,需要關(guān)注類比分?jǐn)?shù),需要關(guān)注從整式的運(yùn)算出發(fā),通過(guò)把分?jǐn)?shù)的分子、分母分別用字母表示出來(lái),實(shí)現(xiàn)一般化抽象,從而分離出“整式除法運(yùn)算”這一特征,發(fā)現(xiàn)像分?jǐn)?shù)“除法運(yùn)算”的式子,通過(guò)一般化的概括得到分式的概念,在得到分式的概念后,類比分?jǐn)?shù)提出分式要研究的內(nèi)容,如性質(zhì)、運(yùn)算等,從而初步完成分式整體研究方案的規(guī)劃。在后續(xù)學(xué)習(xí)中,則分別針對(duì)基本性質(zhì)和各種運(yùn)算進(jìn)行規(guī)則的抽象。
根據(jù)數(shù)學(xué)抽象的要求,系統(tǒng)有序地設(shè)計(jì)抽象步驟,合理設(shè)計(jì)和有效開(kāi)展抽象活動(dòng),可以使學(xué)生充分經(jīng)歷數(shù)學(xué)抽象的過(guò)程,從而積累數(shù)學(xué)活動(dòng)經(jīng)驗(yàn),發(fā)展數(shù)學(xué)抽象能力。
- 初中生世界的其它文章
- 智者無(wú)形 行者無(wú)疆
——江蘇省無(wú)錫市塔影中學(xué)“筑夢(mèng)藍(lán)天”科技社掠影 - 整體認(rèn)知 對(duì)比探究 變式拓展
——蘇科版“統(tǒng)計(jì)圖的選用(1)”教學(xué)設(shè)計(jì)與思考 - 逐夢(mèng)鄉(xiāng)村 愛(ài)灑杏壇
- 讓思維之花盛開(kāi)在初中英語(yǔ)閱讀課堂
——以牛津譯林版《英語(yǔ)》9A Unit 4 Growing up Reading為例 - 把數(shù)學(xué)課上出故事味
——“用一元一次方程解決問(wèn)題”教學(xué)有感 - 基于數(shù)學(xué)核心素養(yǎng)的初中教學(xué)探究
——以同題異構(gòu)課“平行四邊形復(fù)習(xí)課”為例

