基于“微元法”優(yōu)化高中物理解題教學(xué)

姚 明

(江蘇省泰州市姜堰區(qū)蔣垛中學(xué) 225503)

科學(xué)的解題思想與方法是提升學(xué)生解題準(zhǔn)確度與效率的重要保障，強(qiáng)化解題思想在教學(xué)中的滲透是教學(xué)的重點(diǎn)內(nèi)容.微元法作為一種重要的解題思想，在解決某些物理問題的時候，往往會起到化抽象為具體，化繁為簡的作用，是學(xué)生求解物理問題的有力武器.因此，如何在高中物理解題教學(xué)中滲透微元法值得深入探討.

一、“微元法”在運(yùn)動類物理問題求解中的應(yīng)用

運(yùn)動類物理問題是高中物理解題教學(xué)的重要組成部分，其中包括許多非常規(guī)的勻速或勻變速運(yùn)動，此時如果采用常規(guī)的數(shù)學(xué)思想或物理思維，常常很難下手，但是此時如果可以引入與應(yīng)用“微元法”，那么往往可以起到化繁為簡的解題效果.對于運(yùn)動類物理問題的求解，應(yīng)用“微元法”的過程中，需要相應(yīng)地選取微小的時間內(nèi)，確保這個時間范圍內(nèi)的速度保持不會出現(xiàn)過大變化，這時候如果對其路程或位移進(jìn)行求解，常常可以起到另辟蹊徑的作用.雖然將運(yùn)動進(jìn)行了無限分割，相應(yīng)分割后所構(gòu)成的各個元同樣會遵從運(yùn)動方面的各種規(guī)律，最后通過對相應(yīng)的元過程進(jìn)行疊加計算就可以求解有關(guān)物理問題.

例1在水平的湖面上停有一艘船只，船長L，船只重量為M，現(xiàn)有一個質(zhì)量為m的人站立在船頭位置處，如果忽略船只的阻力，試求該人從船頭行走到船尾過程中船只的位移？

解析對于該道物理問題的求解，如果采用傳統(tǒng)的運(yùn)動學(xué)與方法，那么求解難度，但是此時如果可以應(yīng)用“微元法”，配合“整體思想”，那么在解決的時候，可以簡化物理問題，降低求解難度.

解以船只與人這個整體作為研究對象，考慮到人在船只上面走動期間整體系統(tǒng)所受外界的合力為零，所以可以看作整體系統(tǒng)滿足動量守恒基本條件.對人走動的過程進(jìn)行無限分割，那么在特別小的時間△t內(nèi)，可以將人的運(yùn)動過程看作是勻速運(yùn)動，此時可以求得相應(yīng)船只的位移，選擇船和人在任意時刻的速度分別為v1和v2，那么應(yīng)用動量定理進(jìn)行求解后，可得：mv1=Mv2，此時對公式兩邊同乘以Δt，可得：mv1Δt=Mv2Δt.

由于Δt非常小，所以此時可以近似地將船只與人的運(yùn)動當(dāng)做是勻速運(yùn)動，對應(yīng)的船只與人的位移大小則分別為Δs1=v1Δt和Δs2=v2Δt.

綜合上述推導(dǎo)與分析，可知mΔs1=MΔs2.

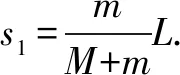
二、“微元法”在電磁場物理問題求解中的應(yīng)用

在電磁場中，導(dǎo)體運(yùn)動期間會受到安培力作用，且相應(yīng)的作用力大小會伴隨著導(dǎo)體運(yùn)動而相應(yīng)地發(fā)生改變，所以導(dǎo)體在磁場中運(yùn)動過程中會出現(xiàn)變化，此時無法直接應(yīng)用勻速或勻變速部分的物理規(guī)律，尤其是還需要綜合考慮重力作用所構(gòu)成的復(fù)合力場.此時如果可以借助“微元法”，將相應(yīng)導(dǎo)體在磁場中的運(yùn)動進(jìn)行無限分割，選取比較小的時間，可以將相應(yīng)的運(yùn)動過程看成勻速運(yùn)動，此時可以直接運(yùn)用相應(yīng)的物理性質(zhì)與規(guī)律，最后再將相應(yīng)過程進(jìn)行疊加后可求得相應(yīng)問題.

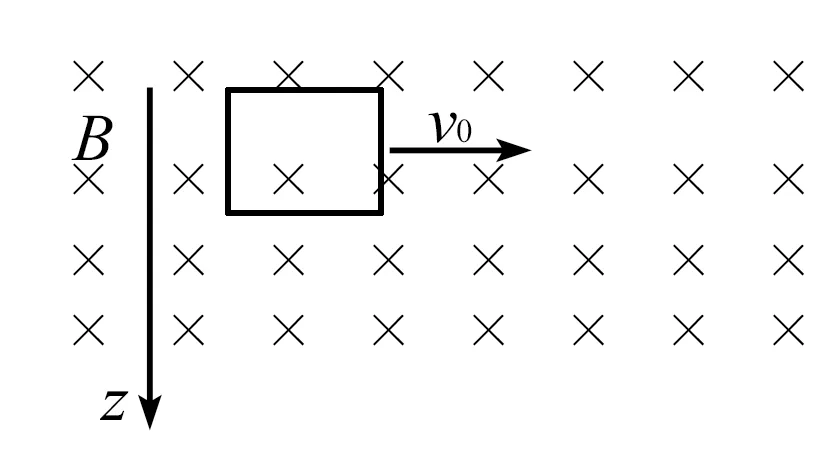
圖1

例2如圖1，在豎直平面中包括一個電阻、質(zhì)量、邊長分別為R、m和L的正方形線框，且平面內(nèi)包括垂直向里的磁場，將該線框以v0初速度水平拋出，線框始終和磁場方向保持相互垂直，且已知磁場磁感應(yīng)強(qiáng)度滿足B=B0+kz.Z軸保持垂直向下，重力加速度為g，試求：(1)在線框豎直方向速度為v1的時候，求其中瞬時電流值？(2)在復(fù)合場中運(yùn)動期間，求線框的最大電功率？(3)如果線框從開始到瞬時速度為v2時候的耗時為t，試求線框的總位移值？

解析針對該道物理問題，由于涉及到導(dǎo)體在磁場中的非均勻變化過程，此時無法直接運(yùn)用勻速或勻變速的相關(guān)物理運(yùn)動規(guī)律，但是如果可以應(yīng)用微元法，將相應(yīng)運(yùn)動過程劃分成無限個非常小的微元塊，那么可以簡化求解過程.

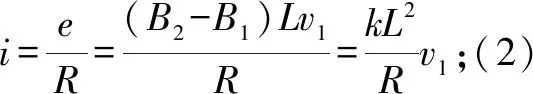
總之，微元法為高中生解決運(yùn)動類或電磁場類等物理問題提供了一個新的思路，在簡化這些復(fù)雜或變化速度運(yùn)動問題方面的應(yīng)用優(yōu)勢非常顯著.在平時的高中物理解題教學(xué)中，教師要結(jié)合相關(guān)的例題，強(qiáng)化學(xué)生對于微元法的認(rèn)識，使他們可以牢固掌握這一有力的解題武器，從而不斷提升他們的解題能力.