函數中“解析式”、“表格”、“圖象”的三位一體教學
侍書麗
(江蘇省蘇州國際外語學校 213151)
數與形是數學中的兩個最古老,也是最基本的研究對象,它們在一定條件下可以相互轉化,數形結合包括兩個方面:一是“以數解形”,二是“以形助數”.初中數學的函數教學中,畫函數圖象是函數中數形結合思想的正式開始,這一思想有一個要求是函數圖象的幾何特征與數量特征緊密結合,所以教學目標是讓學生達到見“數”腦中就要有“形”,見“形”腦中就要有“數”的境界,即實現函數教學中“解析式”、“表格”、“圖象”的三位一體.
一、在初學函數圖象的畫法時精心設計能搭建三者關系的問題
一次函數圖象的畫法是學生第一次學習,他們的認知基礎是小學學習的折線統計圖,如何實現從解析式到圖象的轉換呢?我對畫圖三部曲“列表——描點——連線”是這樣思考的:
案例畫函數y=2x+1的圖象.
(1)精設問——所設問題具有啟發性,引出下一環節
針對函數關系式,設計這樣的三個問題:(1)兩個變量可以取哪些數,即取值范圍是什么?(2)對自變量x每取一個值,對應函數值y與之有怎樣的數量關系?即對自變量x每取一個值,對應函數值y都比x的2倍大1;(3)如果將x取的每一個值與對應的y的值形成一對有序數對,會想到什么?即平面直角坐標系中有序數對與點的關系.
(2)巧過渡——每一環節都有其各自的作用,但又相互聯系,所以過渡要自然
緊接上面的第三問指出:每一個有序數對如何體現呢?數學中,表格最能體現兩個量之間的關系.特別注意的是:列表絕不僅僅是畫圖的一個工具,還是“以數解形”的良好鋪墊,故列好表不用急著畫圖,而是要“駐足”看一看表格中到底蘊含著什么規律?是否有解析式所看不到的東西?

x…-3-2-10123…y…-5-3-11357...
(3)慢思索——每一個結論都要通過探索得到,要能水到渠成
①除了表格兩端的省略號表示還有無數有序數對沒能體現以外,一定要讓學生明白,其實每兩個整數之間也有無數有序數對沒能體現,這樣才能解釋畫出的圖象為何是線.
②每一個有序數對除了y是x的2倍加1外,還要能發現x每增加1,y便增加2.這是為什么呢?是解析式中哪個量引起的呢?這里要讓學生去思考并發現,是由比例系數k決定的,若函數解析式是y=3x+1則表示x每增加1,y便增加3,學生這時會想,若是y=-2x+1呢?這樣做有三個好處:Ⅰ.圖象的兩類不同趨勢就自然在腦中形成了,無需依靠畫一批函數圖象通過觀察歸類而得到,學生多了一層探索和理解,緊緊抓住了問題的本質;Ⅱ.以后有一類題是給出表格中數據,如何判斷是學過的哪一類函數,學生便可依靠x每增加某相同的單位,y也增加或減少另外的某相同的單位來判斷是一次函數;Ⅲ.比例系數|k|可以通過算tanα(其中α是直線與x軸的夾角即坡角)的值來確定,既方便又準確.
③描點、連線過程中,描出第一個點,而準備描第二個點時,一定要讓學生體會x變大時,點便會向右移,而y變大時,點會上移,如此,x變大而y也同時變大時,點會朝右上方移動,這樣學生不難體會朝不同方向時,x、y是如何變化的,學生才會對增減性有一個系統性的認識.而且邊描點時要邊體會每兩個點都是網格中“橫1×豎2”的長方形對角上的兩個點,這樣才會讓學生對圖象是一條直線心服口服.
上面的案例說到底就是講究一個“慢”字和“探”字,著名教育家約翰杜威指出:““慢而穩”才能使印象較為沉著,思維較為深澈,問題感覺得深,思維才能滲透得切,任何教學,僅為報表記憶、夸示嫻熟等,而把問題輕輕掠過,不去深刻思維的都違反了真正的思維訓練的方法.”大多數老師這三步進行的是很快的,因為還要畫更多的圖,然后通過所畫的圖象總結相關的性質,然而我在這一“慢”一“探”中,所有的性質不僅全部形成,而且都是在理解的基礎上形成,學生的思維得到了發散和深入,一幅圖可見無數圖,即見樹木亦見森林.
二、在一定認知基礎上畫圖時要仔細剖析和駐足觀察內在聯系
我認為,只有實現函數教學中“解析式”、“表格”、“圖象”的三位一體,才能真正地實現“數形結合”思想的滲透;只有實現函數教學中“解析式”、“表格”、“圖象”的三位一體,才能更深入地探究復雜函數里的難點問題.例如:二次函數的左右平移問題,本可以通過畫一組函數圖象,可輕松看出平移的規律,但事實上,學生總是覺得奇怪,因為點在坐標系中移動時,若向右移動則點的橫坐標變大,而向左移動則點的橫坐標變小,那按理應該是“左減右加”才對啊.通常老師只會向學生解釋說這兩者是不一樣的,或不厭其煩地再拿出畫的圖讓學生看,事實擺在面前嘛!為了解決這一問題,下面的案例我是這樣設計的:
案例畫出二次函數y1=x2與y2=(x+1)2的圖象.
(1)關系式所體現的數量關系可折射出點的位置關系
學生已經有了畫圖的經驗,是可以快速畫出來的,但是,在畫圖之前,我拋出了一個問題:當兩個函數值取相同的值(正數)時,自變量x的取值有什么聯系?這個問題看似簡單,但一下子讓學生有了思考并發現:第二個函數自變量x的兩個取值分別比第一個的兩個小1,有了這個思考,其實已經為后面的研究埋下伏筆,已經能夠理解后面的結論了.
(2)表格所體現的點的位置關系可折射出圖象位置關系
所列表格如下:
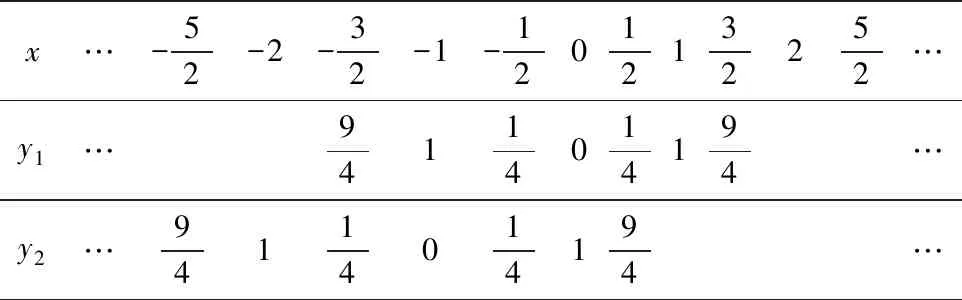
x…-52-2-32-1-12012132252…y1…94114014194…y2…94114014194…
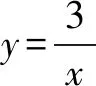
我國數學家華羅庚說過:“數形結合百般好,割裂分家萬事休!”結合上面的兩個案例,都足以說明函數關系式、表格和圖象之間成一一對應的關系,這種一一對應想要有機結合,需要我們一一去探究并通過設問架起搭在它們之間的橋梁,而不是在已經完成了的“成品”上觀察歸納,這樣會使學生越來越把記結論變得理所應當,而失去了學習數學的興趣,更失去了數學本身的意義了.

