N 種群Gilpin-Ayala 脈沖競爭模型正周期解存在性和全局吸引性

路 杰

(宿州職業技術學院基礎教學部，安徽 宿州 234101)

引 言

考慮以下具脈沖的N 種群Gilpin-Ayala 競爭模型［1-4］:

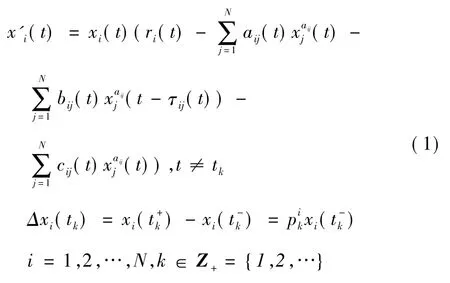
其中，xi(t) 表示種群Xi在t 時刻的密度; ri(t) 表示種群Xi在t 時刻的內稟增長率［5］; aij(t) ，bij(t) (i ≠j) 表示種群xi和xj間的競爭，Tij(t) 表示時滯，并且T =表示對種群內相互影響的非線性衡量，aij(i ≠j) 表示對種群間相互影響的非線性衡量，aij是正常數; ri(t) ，aij(t) ，bij(t) ，cij(t) ，τij(t) ，i，j = 1，2，…，N(都是R 上的T-周期連續函數; aij(t) ，bij(t) ，cij(t) ，τij(t) ，i，j = 1，2，…，N 都非負; aij都是正常數;食餌的內稟增長率ri(t) 可能為負，但滿足的條件是都是正的。R，tk＜tk+1，k ∈Z 均為常數，并且存在正整數q ＞0，使得此外，假設通過人工的作用，種群密度的增長率可能為正，故0。記xi，t0: ［－ τ，t0］→R 為連續函數，再記X(t) =(x1(t;t0，x1，t0) ，…，xN(t;t0，xN，t0) ) 是系統式(1) 需滿足以下初始條件

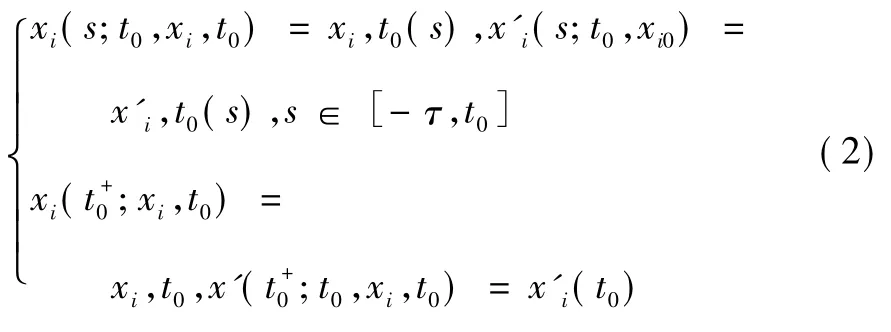
的解，可見系統式(1) 滿足初始條件式(2) 的解X(t) =X(t;t0，xt0) 是分段連續函數，在不連續點tk，k ∈z 是左連續的，即:

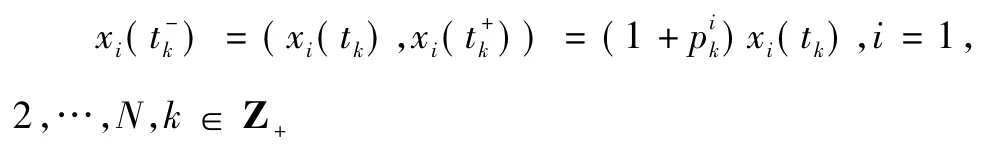
定義1如果存在正常數hi和Hi，使得系統式(1)的每個正解x = (x1(t) ，x2(t) ，…，xN(t) ) 滿足:

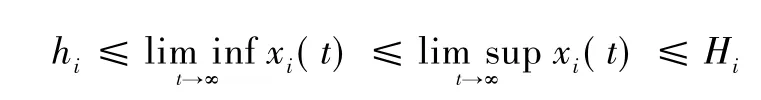
則系統式(1) 是持久的［6］。

特別地說明:下文中將出現的H1、H2、H3和H4是指Hi中當i 分別為1、2、3、4 時的正常數。

1 主要引理

給定函數α(t) ，β(t) ∈PC'ω，β(t) ＞0，考慮以下脈沖系統:

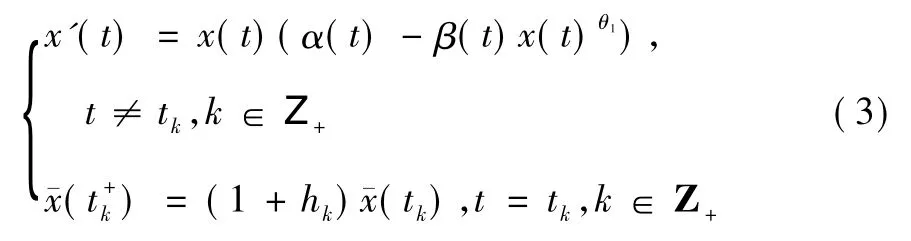
其中，θ1是正常數，hk+q= hk(k ∈Z+) 是常數，并且滿足1 + hk＞0(k ∈Z+) 。

引理1［7］設L 是一個指標為零的Fredholm 映射，N 在上是L-緊的，并滿足下列條件:

(1) 對任意的λ ∈(0，1) ，方程Lx= λΝx的解滿足

引理2［8］若是相對緊的充分必要條件是:

(Ⅰ) 有界，即對任意的x ∈F，存在M ＞0，使得:

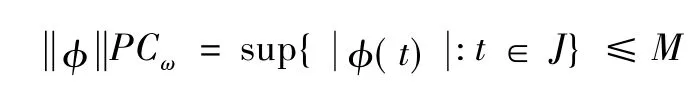
(Ⅱ) F 在J 上是擬-等度連續的。

引理3［9］若φ ∈PC'ω，則:

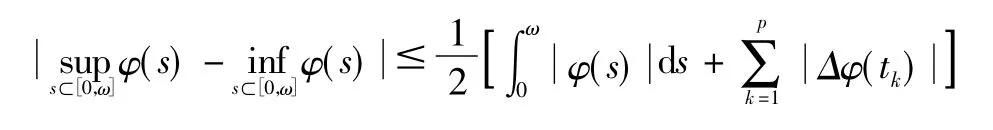
引理4(脈沖型barbǎlat 引理)［10］非負函數f ∈且若對任意的ε ＞0 和n ∈N，存在δ ＞0，當s1，s2∈(tn－1，tn］，時，有則

引理5［11］系統式(1) 有唯一的正周解［12］的充分必要條件是

引理6［11］設a(t) ，b(t) ∈PC'ω，b(t) ＞0 并且若使得:

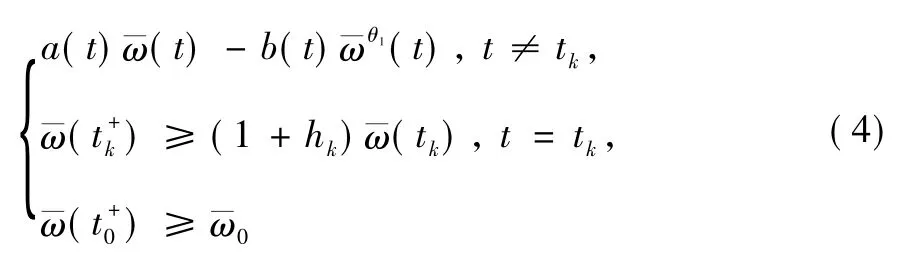
類似有:

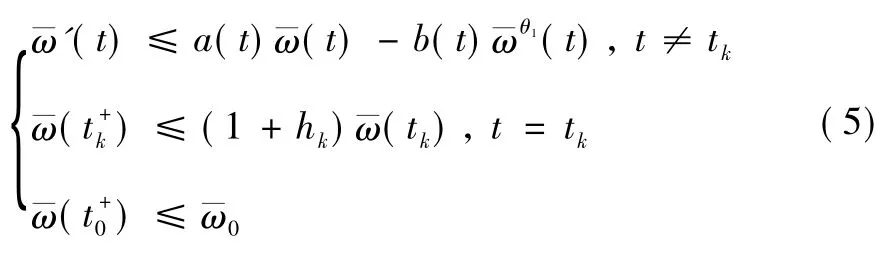
由引理5 和引理6 知θ［a，b］是以下系統:

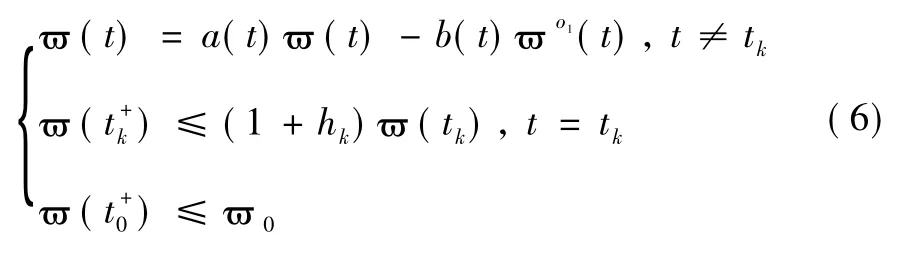
唯一的正周期解。

下面討論系統式(1) 、系統式(2) 的持久性。

引理7若系統式(1) 、系統式(2) 滿足以下條件(H1) :

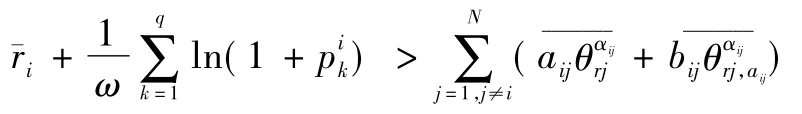
則系統式(1) 、系統式(2) 具有持久性(僅驗證引理7) 。

證明由系統式(1) 、系統式(2) 得

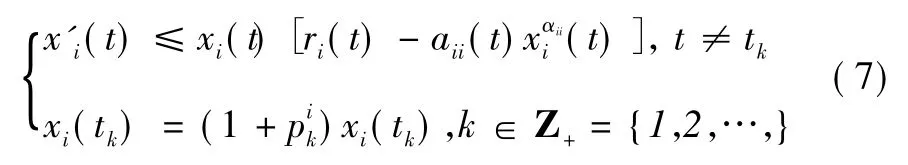
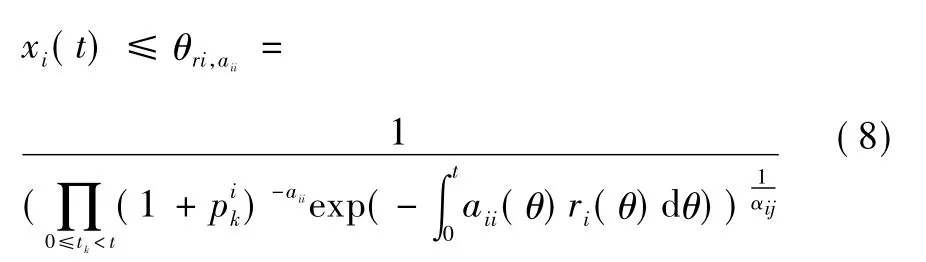
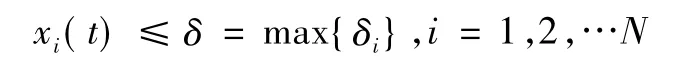
因此有:

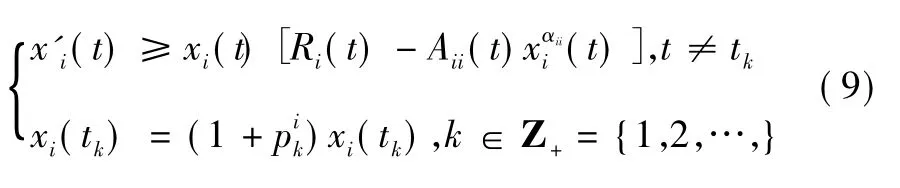
其中:

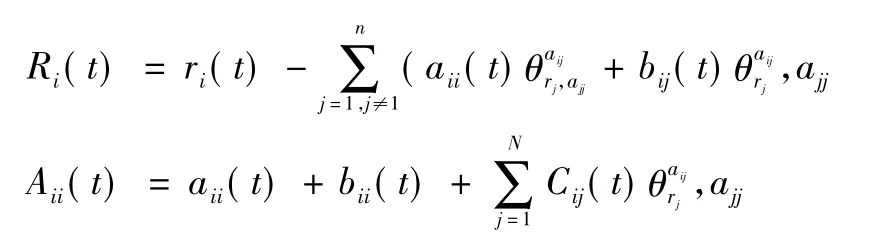
當t 充分大，再由引理6 及引理7 的條件(H1) 得:

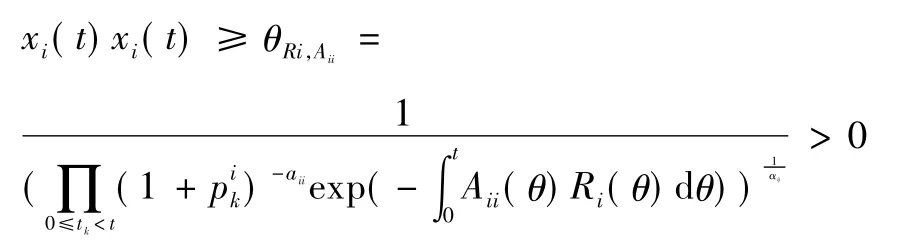
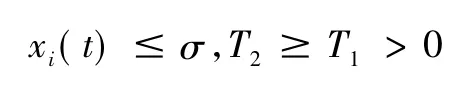
則有:

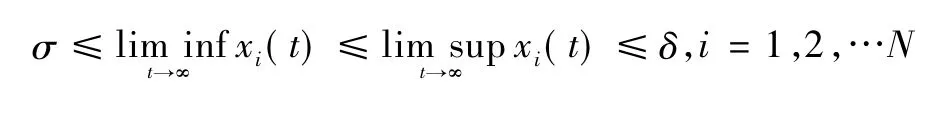
則引理7 得證。

2 主要定理

定理1若以下條件滿足:

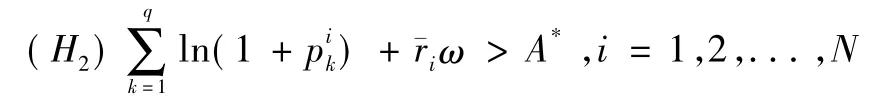
其中:

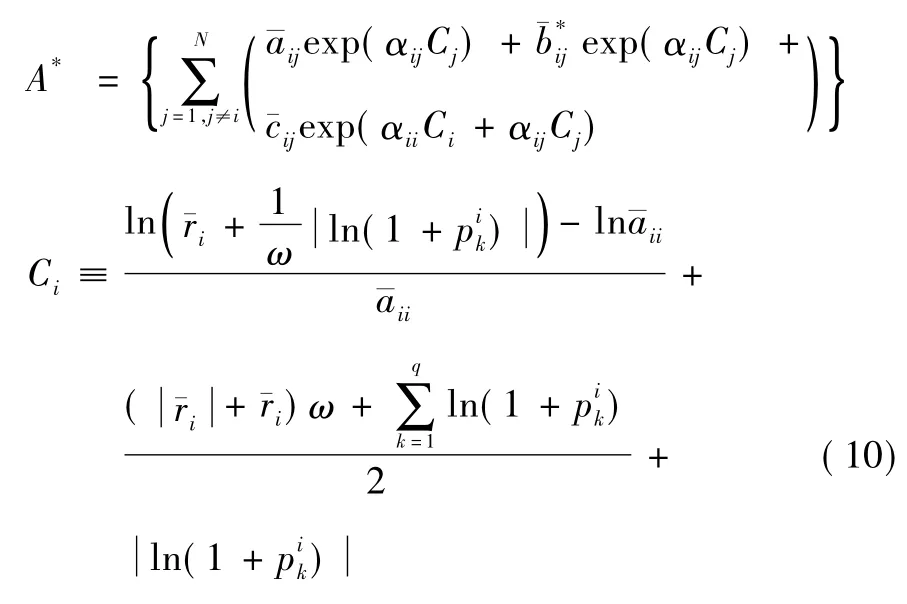
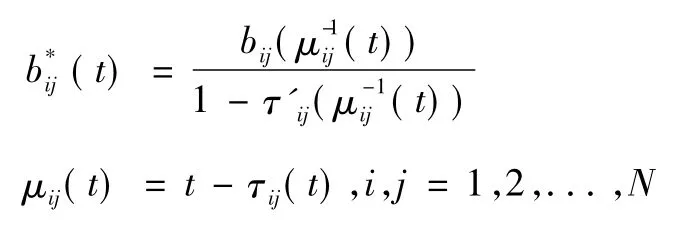
則系統式(1) 與式(2) 至少有正的ω-周期解。

證明令xi(t) = exp(yi(t) ) ，i = 1，2．．．，N，則系統系統式(1) -式(2) 變為:

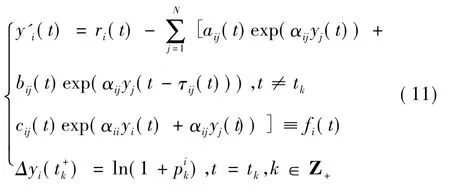
令:

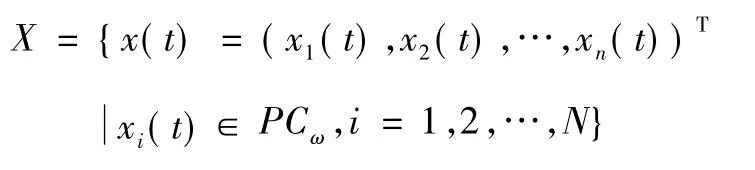
其模為:

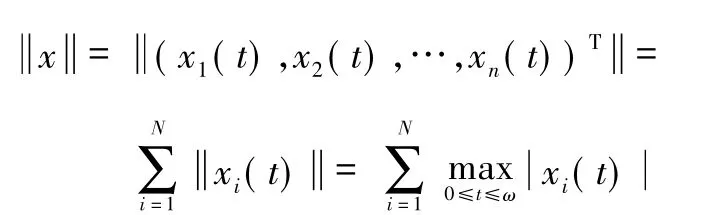
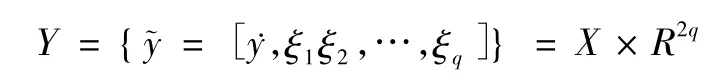
其中:

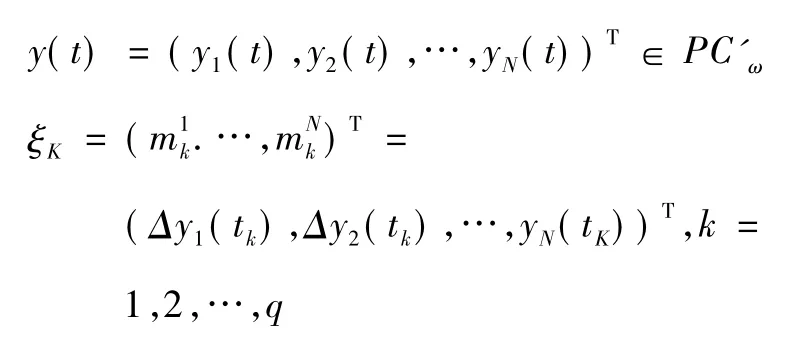
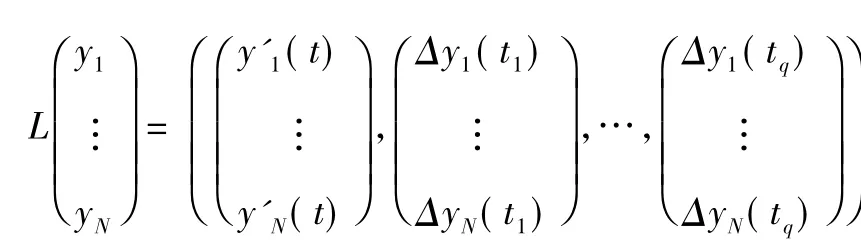
其中:

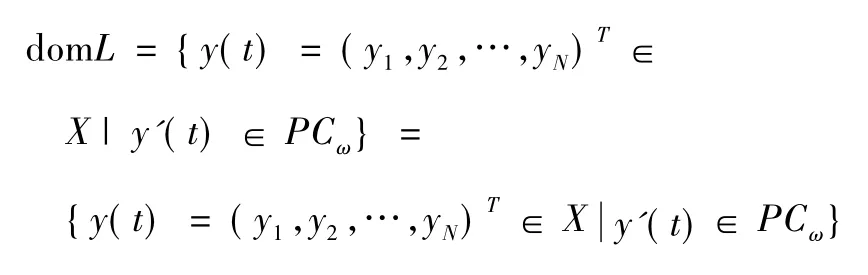
及:

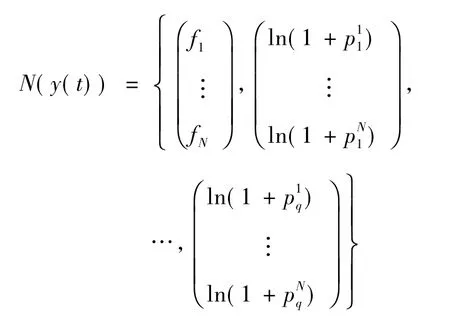
定義2 個投影算子為p:X →X:

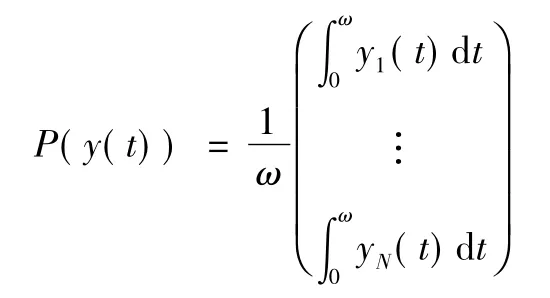
及Q:Y →Y 為:

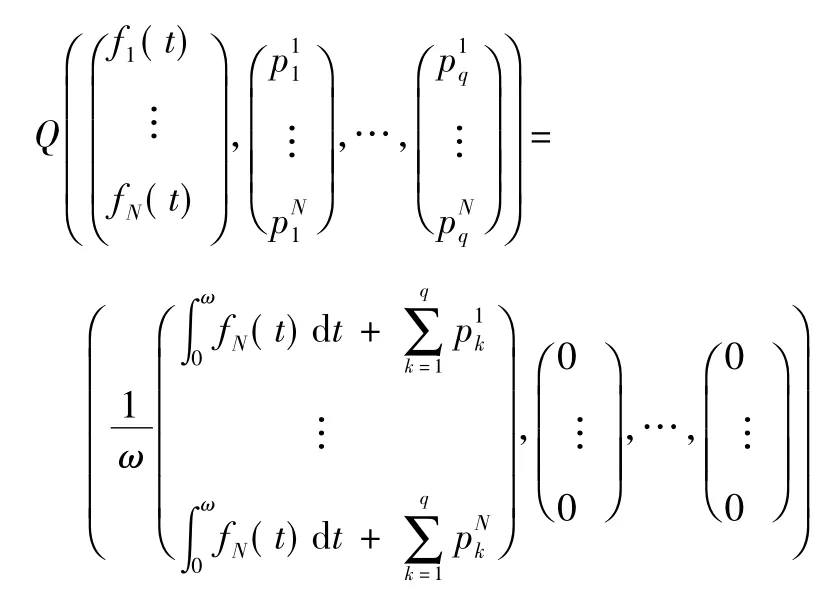
和:

為Y 中2 個閉集，并且有dim KerL = co dim lmL = N，故L 是一個指標為0 的Fredholm 算子。進一步可得L 的廣義逆有如下形式:

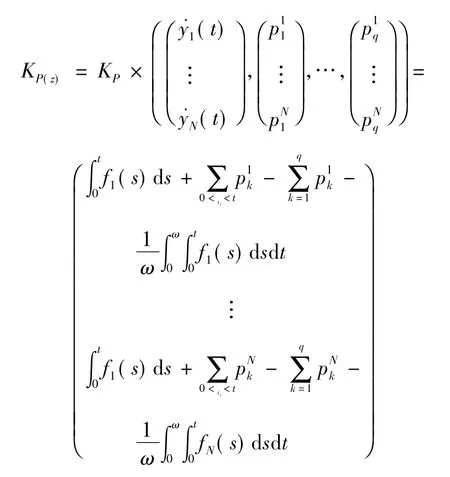
則有:

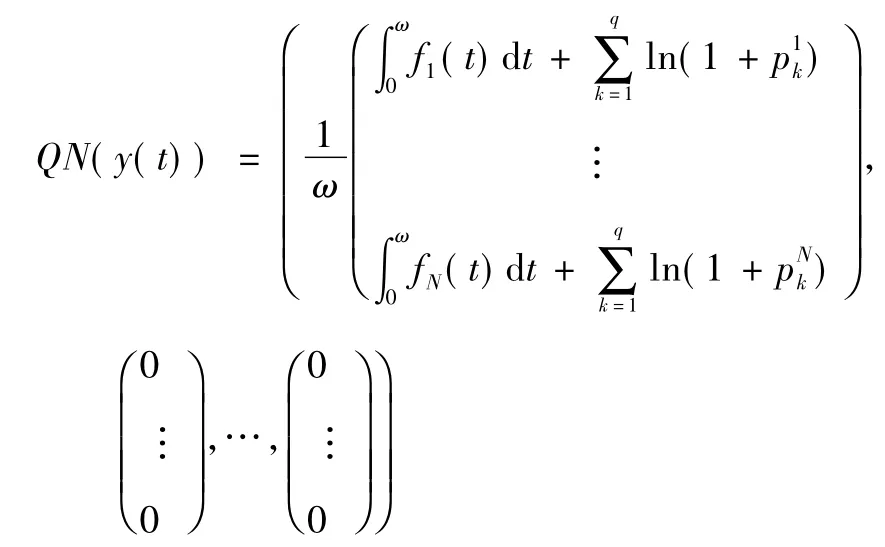
和:

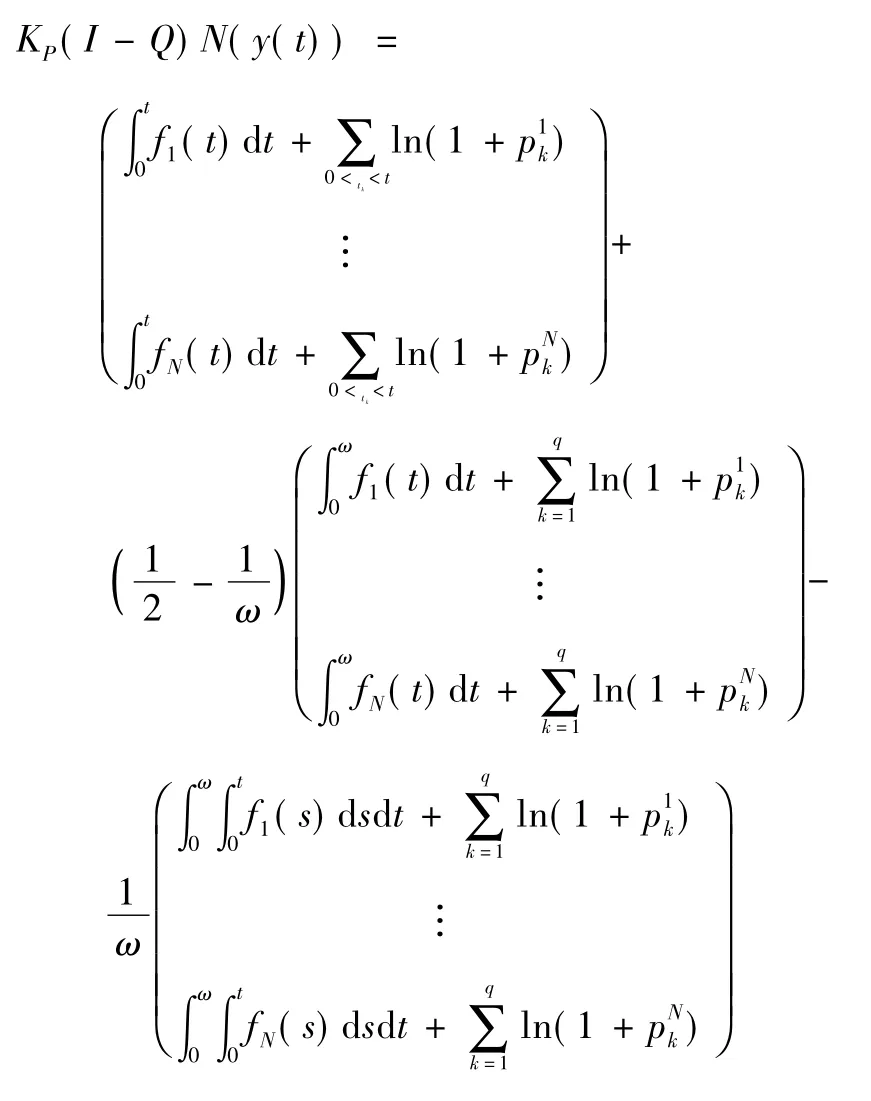
則易得:

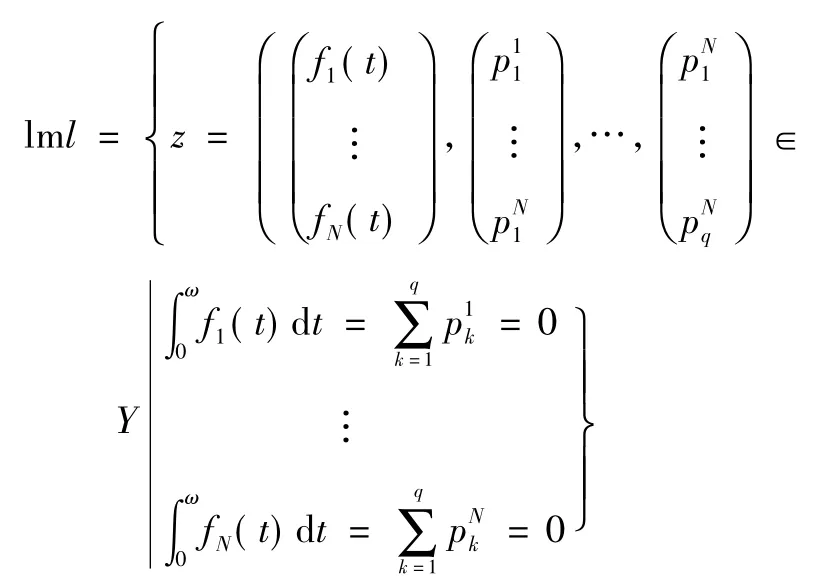
由Lebesqe 控制收斂定理，可得算子QN 和Kp(1 －Q) 都連續。

下面，尋找引理1 所要求的合適的有界開子集。

考慮算子方程:

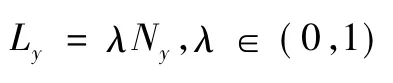
有:

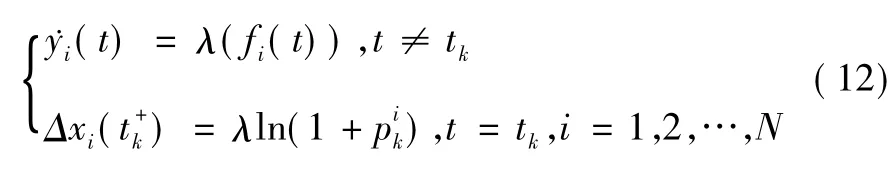
其中:

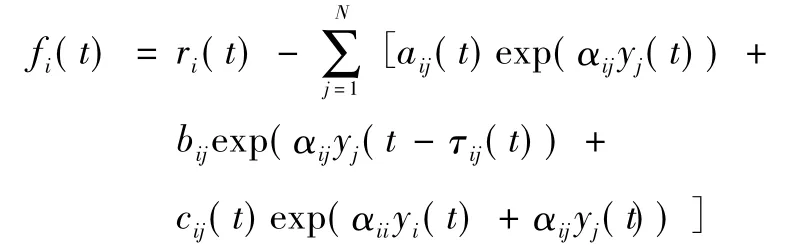
假定對:

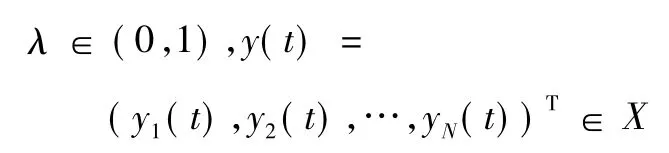
是系統式(12) 的一個周期解，在［0，ω］上積分式(12) 得:

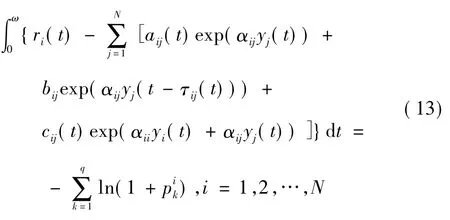
則:

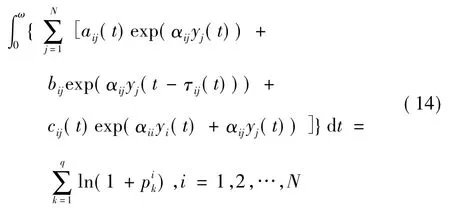
由式(12) 和式(14) ，得

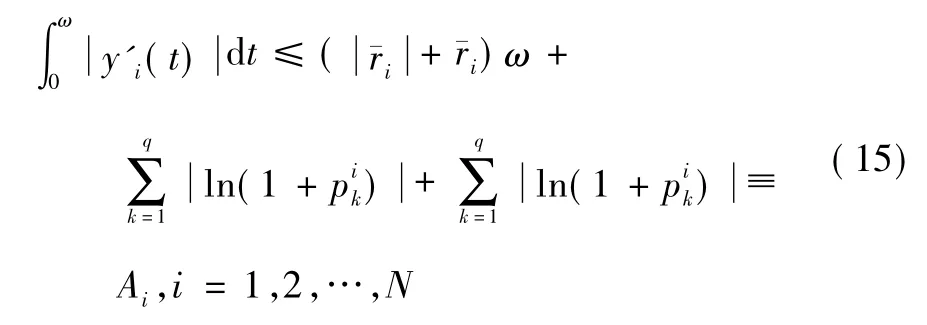
注意到y = (y1(t) ，…，yN(t) )T∈X，則存在ξi，ηi∈［0，ω］，i = 1，2，…，N，使得:

由式(14) 和式(16) 得:

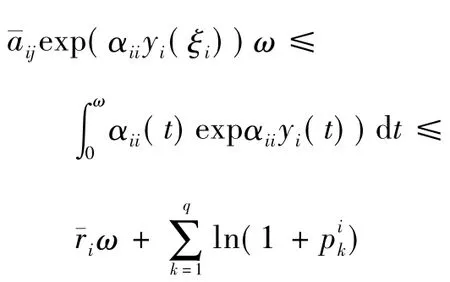
這說明:

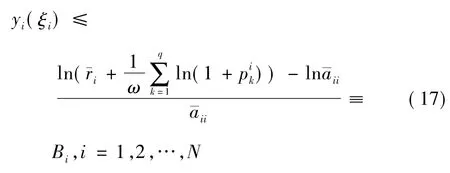
由式(12) 和式(17) 及引理3 得:

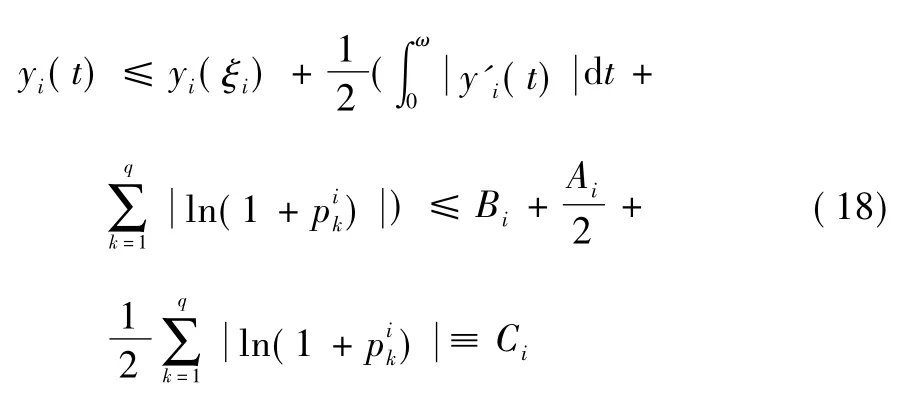
特別地，有:

另一方面，由式(12) 、式(14) 和式(18) 得:

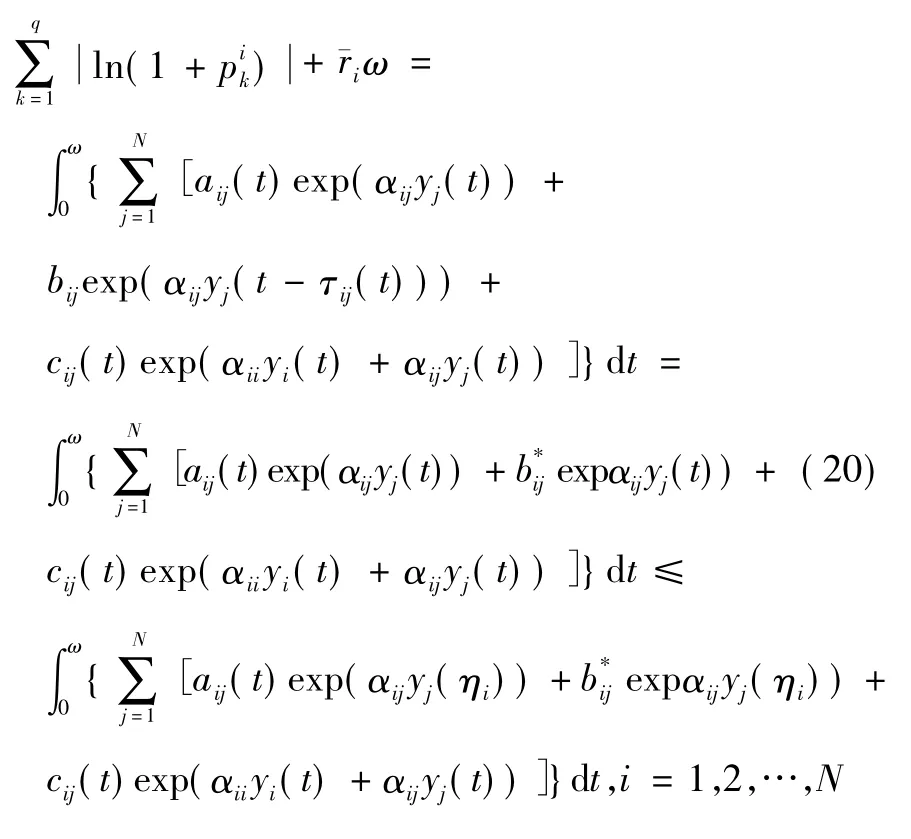
其中:

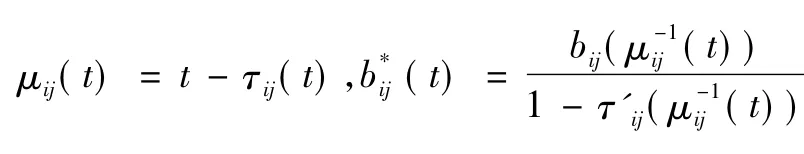
故:

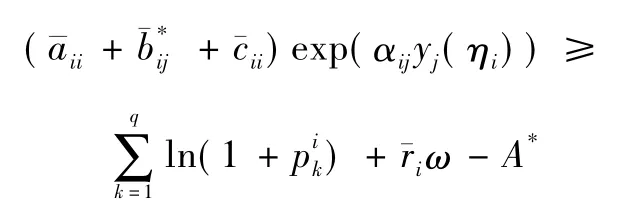
其中:

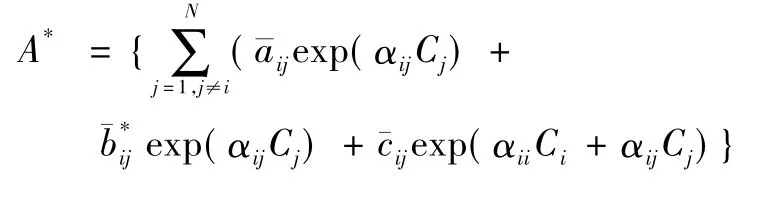
由假設條件(H1) ，得:

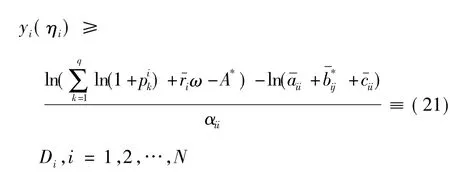
由式(12) 及引理3，得:

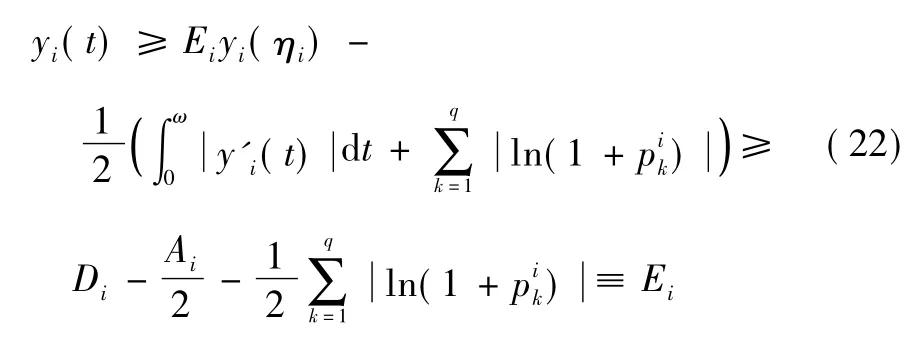
由式(19) 和式(22) ，得:

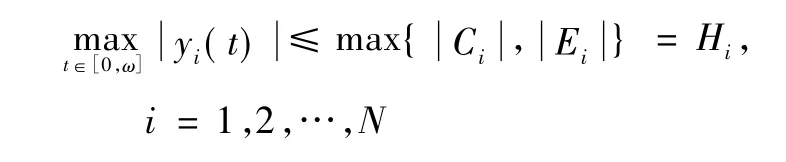
易見H 與λ 無關。

取H = max{H1，H2，…，HN} +c，其中c 是一充分大的正常數，使得下述系統:

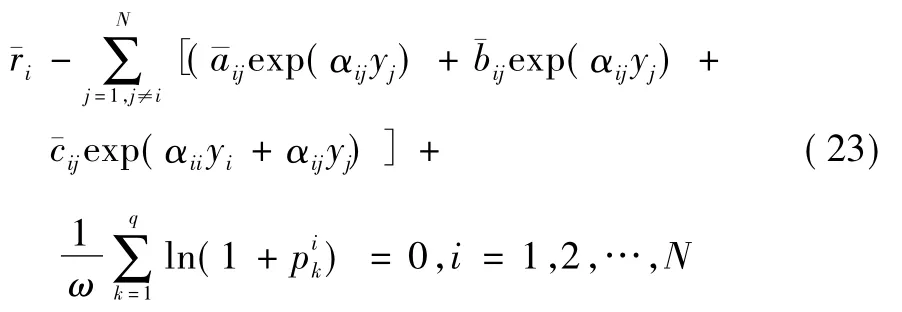
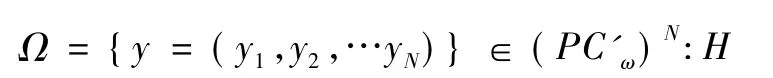
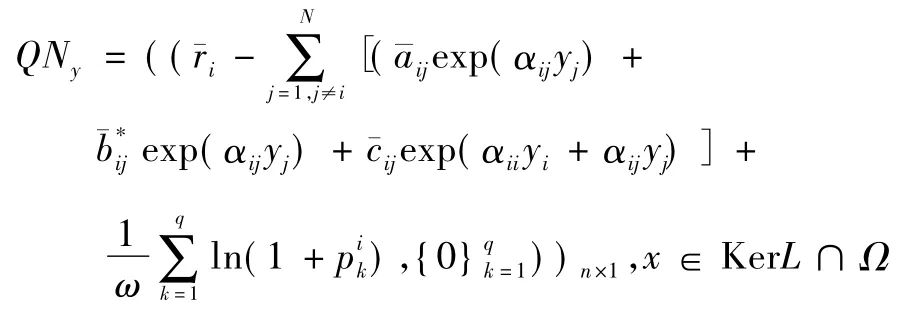
則:

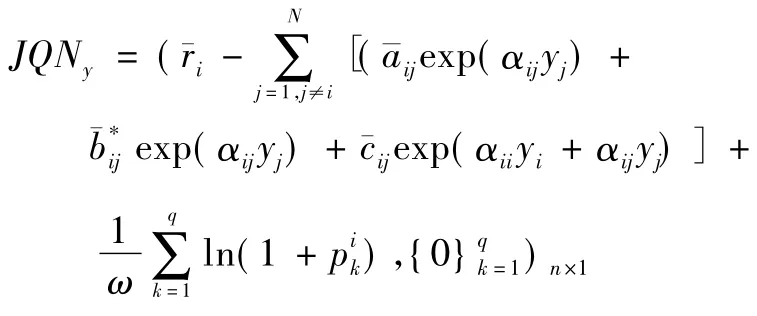
經計算得:

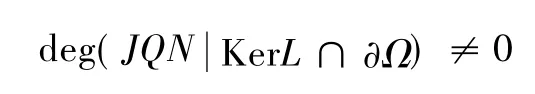
其中，由lmQ = KerL 得J 是恒等映射，這樣Ω 滿足引理1的所有假設條件。由引理1 知系統式(2) 至少有一個ω周期解滿足條件

下面，介紹系統式(1) -式(2) 的正ω-周期解全局吸引性。

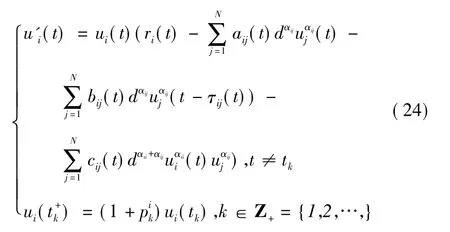
很明顯，系統式(1) -式(2) 和系統式(24) 等價。下面只討論系統式(24) 的ω-周期解全局吸引性。

定理2若條件(H1) 和(H2) 及以下條件都滿足:

(H3) aii≥max{αij}，i，j = 1，2，…，N;

(H4) 存在正常數。

θi，i = 1，2，…，N，d(0 ＜ d ＜ σ) 及ζ 使得其中其中有:

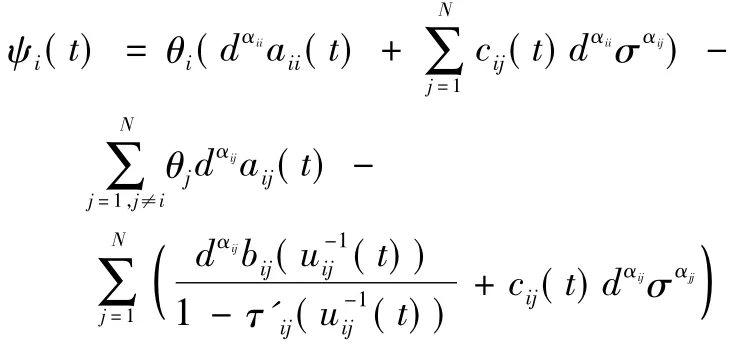
則系統式(1) -式(2) 有唯一全局吸引的周期解x(t) 。

證明取系統式(24) 的一個周期解(u(t) ，u1(t) ，…，uN(t) ) ，即任意一個解(v(t) ，v1(t) ，…，vN(t) ) 由引理3 和定理1 及0 ＜d ＜σ 知存在T0＞0，使得:

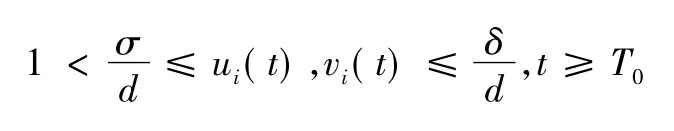
考慮Lyapunov 泛函:

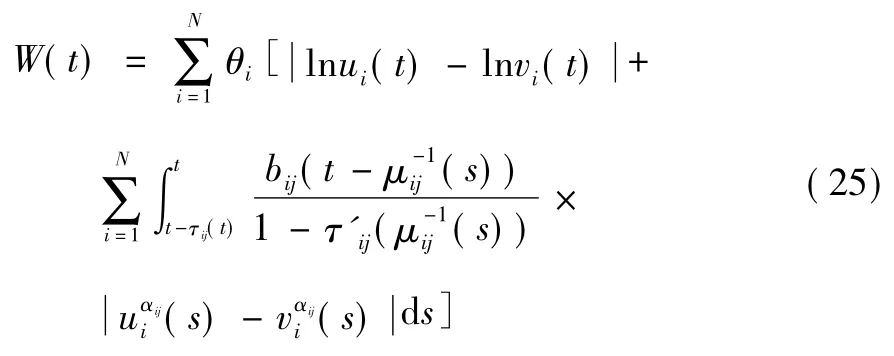
經計算W(t) 沿系統式(25) 的右上導數D+W(t) 得:

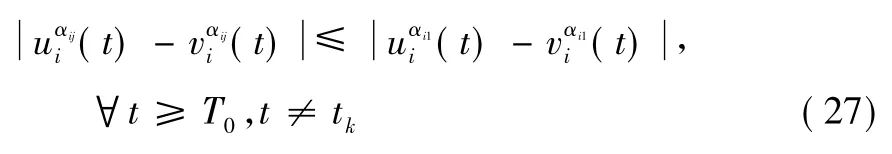
故當t ≥T0，t ≠tk，由系統式(26) 和系統式(27) 得:

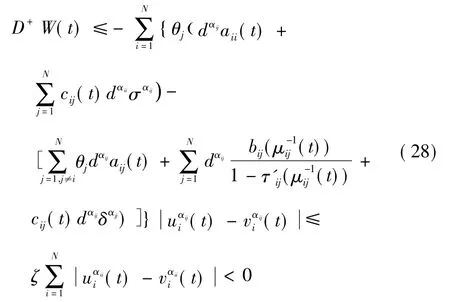
另一方面當t = tk，有:

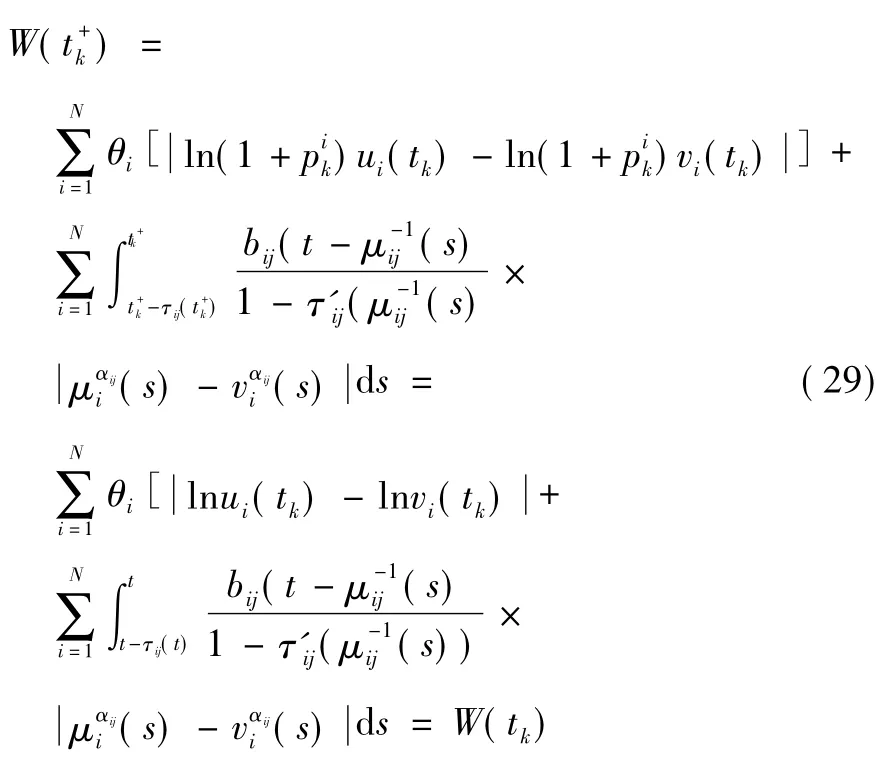
由式(28) 和式(29) 得:

D+W(t) ≤0，t ∈R，t ∈R，t ≠tk，ΔW(tk) ≤0在［T0，t］上積分式(28) 得:

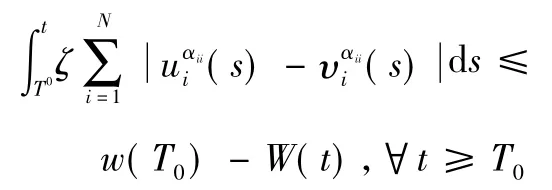
故有:

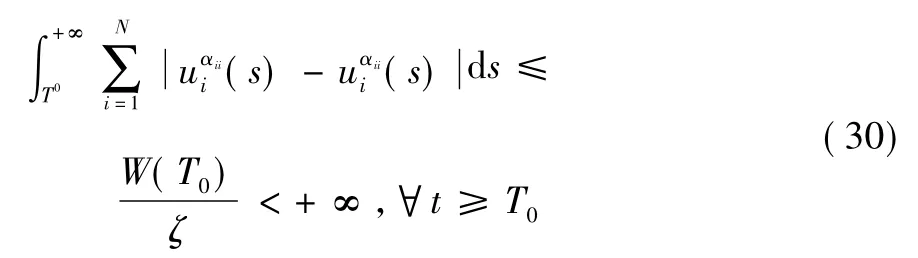
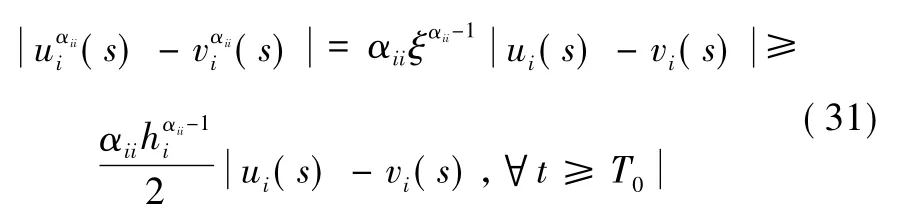
則由引理4 得:

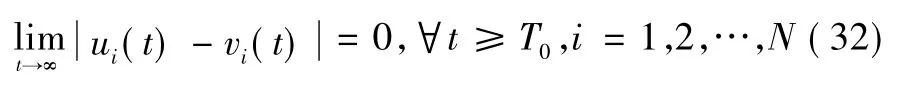
這說明系統式(24) 的全局吸引性。再由式(24) 和系統式(1) -式(2) 的等價性，說明系統式(1) -式(2) 的周期解是全局吸引的。進一步地，存在正數M = min{Mi}使得:

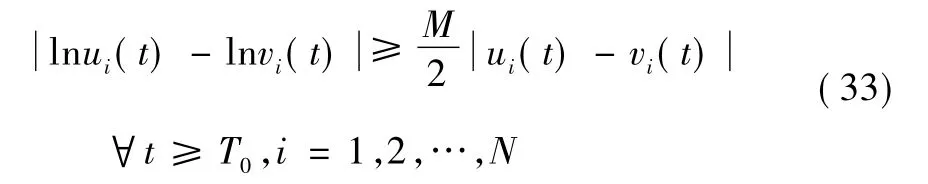
從而有:

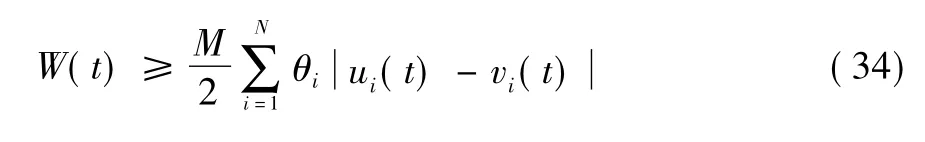
類似以上討論可得到系統式(1) 與式(2) 的周期解全局漸近穩定［13-17］且唯一。

3 例題驗證

考慮系統:

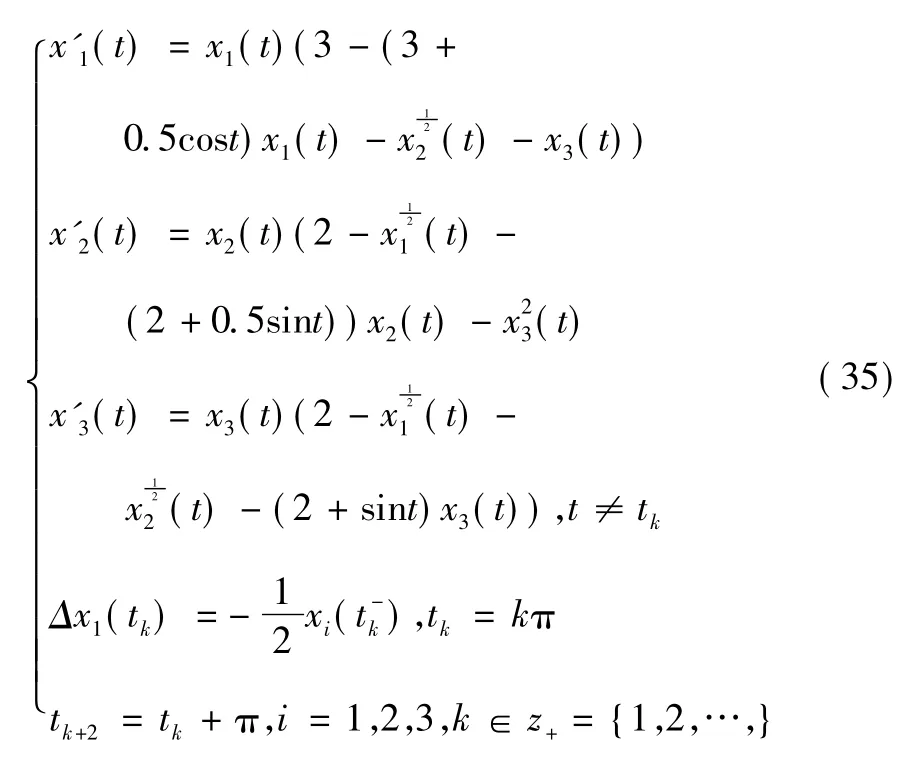
這可驗證定理1 和定理2 的條件均滿足，故系統式(35)的周期解有持久性和全局吸引性［16］。

4 結束語

研究了一類具脈沖的N-種群Gilpin-Ayala 競爭模型解的存在性和全局吸引性證明，給出一個實例說明主要結論的可行性，為一類具脈沖的N-種群Gilpin-Ayala競爭模型研究和實際生產中捕食-食餌模型運用提供了理論依據，在國民生產中具有重要的現實意義。