復形的C-Gorenstein 投射維數

何東林，李煜彥

(隴南師范高等專科學校數信學院，甘肅 隴南 742500)

引 言

Gorenstein 同調理論是相對同調代數的重要內容。1969年Auslander 和Bridger 討論了雙邊Noether 環上有限生成模的G-維數［1］。1995年Enochs 和Jenda 給出任意環上Gorenstein 投射模的概念［2］。Gorenstein 投射模有許多與投射模類似的性質，很多研究者對其進行了推廣［3-7］。特別地，Bennis 等［3］給出了X-Gorenstein 投射模的概念和若干性質。孟凡云等［8］對這一概念做了進一步研究。這方面有關復形和復形每個層次上模的關系的研究是一個重要課題。Enochs 和Garcia Rozas［9-10］證明在Gorenstein 環R 上，復形X 是Gorenstein 投射復形當且僅當模Xm是Gorenstein 投射模(對任意m ∈Z) 。楊剛［11］研究了一般結合環上復形的Gorenstein 投射性及Gorenstein 投射維數。

受上述相關結論的啟發，本文主要介紹并研究復形的C-Gorenstein 投射維數。文中的環R 均指有單位元的結合環，模指酉模。C 表示一個關于直和封閉且包含所有投射模的左R 模類。左R 模復形…→X－1→X0→X1→X2→…記為X，用Y 表示R 模復形組成的Abel 范疇，顯然該范疇有足夠的投射對象和內射對象。對任意復形C 和D，用Hom(C，D) 表示C 到D 的同態群，Exti(C，D) 表示由Hom(C，D) 導出的第i 個同調群，C#表示形如C ≡…→C－1→C0→C1→C2→…的正合復形組成的類，其中Ci∈C。其余未涉及的概念和記號見文獻［12 －15］。

1 定 義

定義1［8］稱左R-模M 是C-Gorenstein 投射模，如果存在正合列:

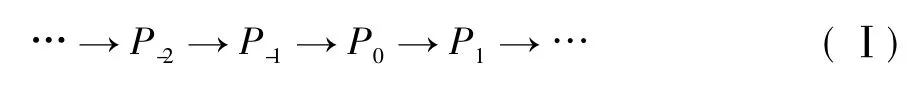
其中，Pi為投射模; M = Ker(P0→P1) 且對任意H ∈C有正合列式(Ⅰ) 在函子HomR(－，H) 仍正合; 用CGP表示所有C-Gorenstein 投射模組成的類。

定義2稱左R-模復形X 是C-Gorenstein 投射復形，如果存在復形正合列:

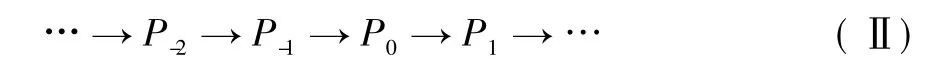
其中，Pi為投射復形，X = Ker(P0→P1) 且對任意復形C ∈C#，該正合列在Hom(－，C) 下仍正合。

定義3設X 為左R-模復形，X 的C-Gorenstein 投射維數定義如下:

inf{n| 存在正合列0 →Gn→…→G1→G0→X →0，其中Gi為C-Gorenstein 投射復形}，記為C-Gpd(X) 。如果這樣的n 不存在，則規定C-Gpd(X) = ∞。

2 主要結果

定理1設X 為左R-模復形，則以下條件等價:

(1) X 是C-Gorenstein 投射復形;

(2) 每個層次上的模Xm是C-Gorenstein 投射模。

證明由定義1 和定義2 易證。

圖1 復形正合列展開圖

由Xm+1是C-Gorenstein 投射模，且Ii－1是C 中模M的一個上合沖，易知Ext1(Xm+1，Ii－1) = 0。因此R-模正合列可裂，從而存在g:Bm+1→Ii－1，使得gαm+1= 1。令其中βm=且βn= 0(n ≠m，m －1) ，則β 為復形同態，且βα =1，從而復形正合列X →0 可裂，且因此對任意i ≥1 有

對任意C ∈C#，由于C 關于直和封閉，所以C 是形如的復形的直和。因此對任意i ≥1 和任意復形C ∈C#，有Exti(X，C) = 0。

因為每個層次上的模Xm是C-Gorenstein 投射模，所以Xm是Gorenstein 投射模。顯然Xm具有投射預包絡。由文獻［11］中引理2 可知復形X 具有投射預包絡。不妨設γ0:X →P0是X 的投射預包絡，易知γ 為單同態。考慮正合列0 →X →P0→H1→0，其中H1= Co kerγ0。由于γ0是X 的投射預包絡，且對任意C ∈C#有正合列有:

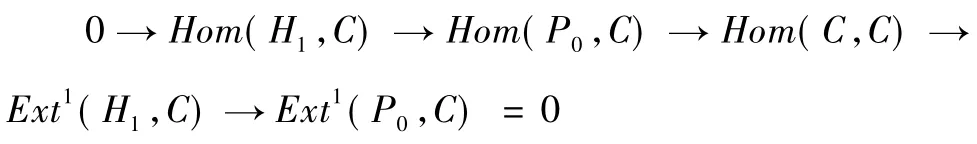
因此Ext1(H1，C) = 0。因為對任意N ∈C，有所以不妨考慮第m 個層次0 →Xm→由是C-Gorenstein 投射模易得是C-Gorenstein 投射模。類似地考慮H1的投射預包絡，繼續上面的討論，一直進行下去可得正合列:

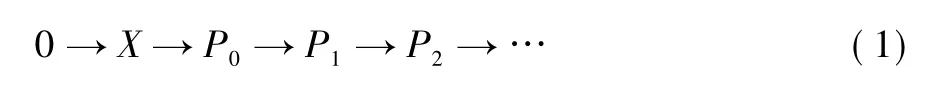
其中，Pi為投射復形，且對任意復形C ∈C#正合列式(1) (在HomR(－，C) 仍正合。

考慮由投射覆蓋導出的如下復形正合列:

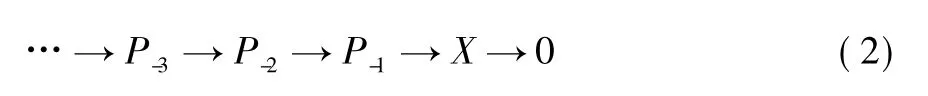
因為對任意i ≥1 和任意復形C ∈C#，有Exti(X，C) =0，所以式(2) 在HomR(－，C) 正合。由(1) 、式(2) 拼接可得復形正合列式(Ⅱ) ，其中，Pi為投射復形，X =Ker(P0→P1) 且對任意復形C ∈C#有正合列式(ε) 在HomR(－，C) 下仍正合。因此X 是C-Gorenstein 投射復形。

定理2設X 為左R-模復形，則

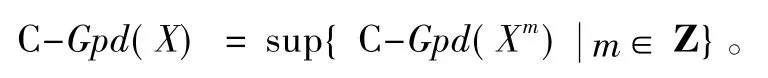
證明先證若sup{ C-Gpd(Xm) | m ∈Z} = ∞，則不等式顯然成立。若sup{ C-Gpd(Xm) | m ∈Z} = n 有限，則考慮復形X 的投射分解:

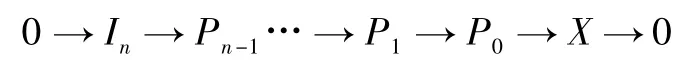
其中，Pi為投射復形。考慮第m 個層次:

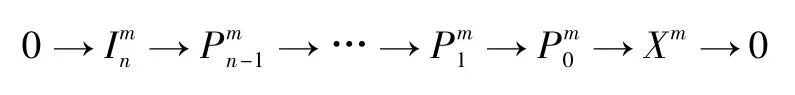
注意到C-Gpd(Xm) ≤n。由文獻［8］中命題3．14得是C-Gorenstein 投射模。又由定理1 知In是CGorenstein 投射復形。因此C-Gpd(X) ≤n，即:

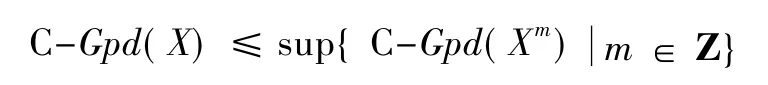
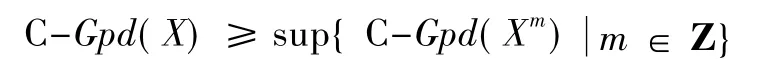
命題1設X 為左R-模復形且C-Gpd(X) = 0，則存在復形正合列: 0 →H →G →X →0 和0 →X →H'→G'→0，其中G，G'為C-Gorenstein 投射復形，H，H'為投射復形。

證明因為C-Gpd(X) = 0，即X 是C-Gorenstein 投射復形，由定義1 知存在復形正合列… →P－1→P0→P1→…(ε) ，其中Pi為投射復形，X = Ker(P0→P1) 且對任意C ∈C#有序列式(Ⅱ) 在Hom(－，C) 下正合。取G = lm(P0→P1) ，顯然G 為C-Gorenstein 投射復形。易知正合列0 →0 →X →X →0 和0 →X →P0→G →0 是滿足要求的正合列，因此結論成立。

定理3設X 為左R-模復形且C-Gpd(X) = n(n≥1) ，則存在復形正合列: 0 →H →G →X →0 和0 →X →H'→G'→0，其中，G，G'為C-Gorenstein 投射復形，pd(H) ≤n －1 且pd(H') ≤n。

證明對n 用數學歸納法。當n = 1 時，存在正合列0 →Q1→Q0→X →0，其中Q0，Q1為C-Gorenstein 投射復形。對Q1用命題1 可得存在復形正合列0 →Q1→H0→G0→0，其中，G0為C-Gorenstein 投射復形，H0為投射復形即pd(H0) = 0。考慮每個層次上的推出圖及對應的復形交換圖分別如圖2 和圖3 所示。

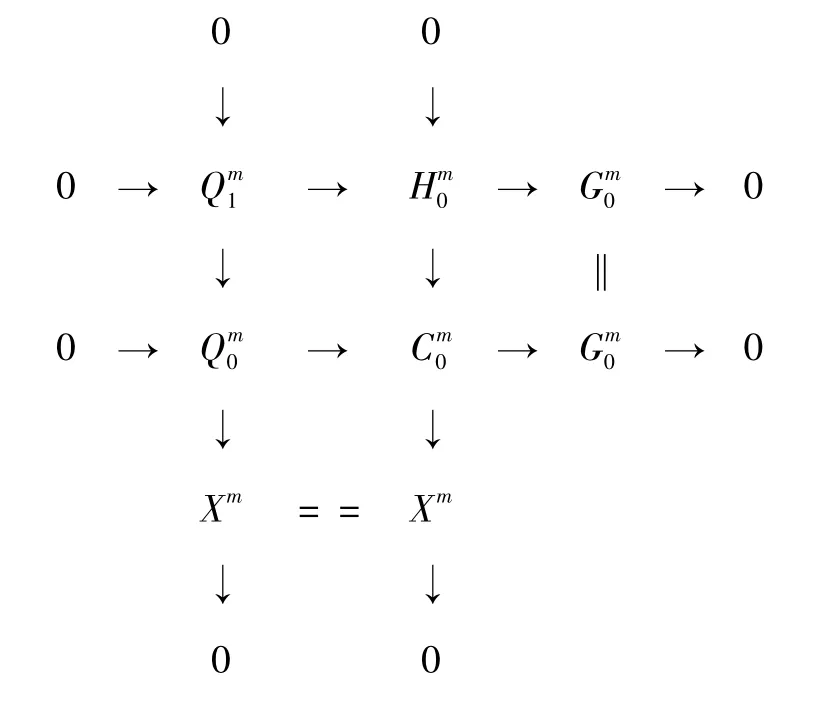
圖2 和的推出圖

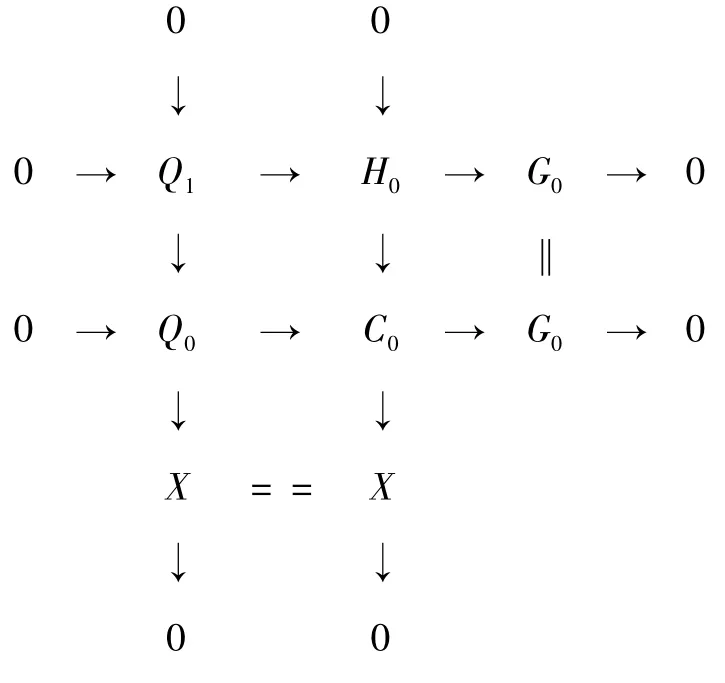
圖3 與圖2 對應的復形交換圖

注意到在正合列0 →Q0→X0→G0→0 中Q0，G0為C-Gorenstein 投射復形，易得X0為C-Gorenstein 投射復形。可見0 →H0→X0→X →0 是滿足要求的第一個正合列。對X0用命題1 知，存在復形正合列0 →X0→H1→G1→0，其中G1為C-Gorenstein 投射復形，H1為投射復形。考慮每個層次上的推出圖及對應的復形交換圖分別如圖4 和圖5 所示。

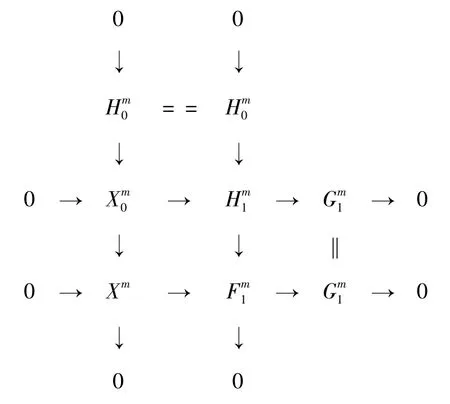
圖4 和的推出圖

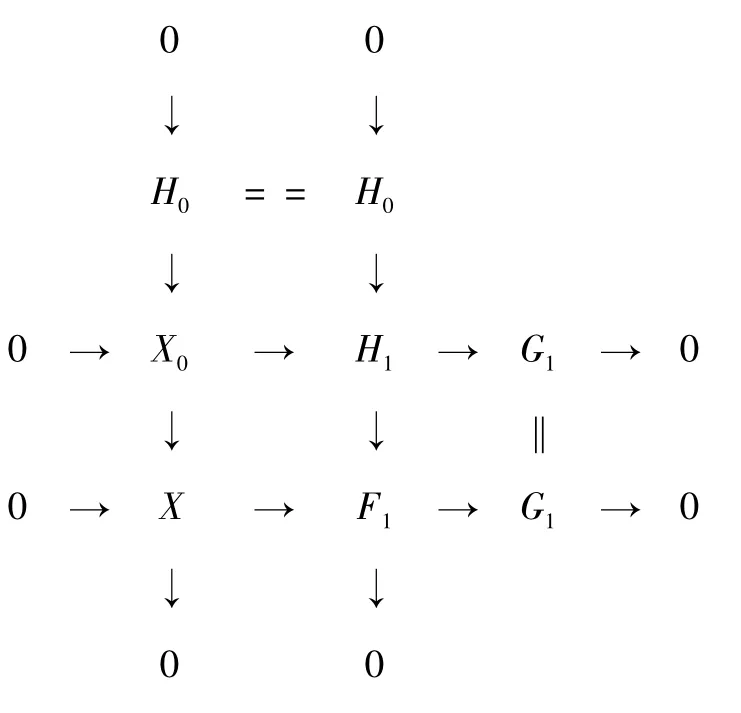
圖5 與圖4 對應的復形交換圖

由H0，H1是投射復形得pd(F1) ≤1，從而序列0 →X →F1→G1→0 是滿足要求的第二個復形正合列。

假設結論對n －1 成立，下證結論對n 也成立。設X為左R-模復形且C-Gpd(X) = n。

則存在復形正合列0 →Qn→Qn－1→…→Q1→Q0→X →0，其中Qi為C-Gorenstein 投射復形。令K0= Ker(Q0→X) ，則有兩個正合列: 0 →Qn→Qn－1…→Q1→K0→0 和0 →K0→Q0→X →0。可見C-Gpd(K0) = n －1。

由假設知存在正合列0 →K0→Hn－1→Gn－1→0，其中Gn－1為C-Gorenstein 投射復形，pd(Hn－1) ≤n －1。考慮每個層次上的推出圖及對應的復形交換圖分別如圖6和圖7 所示。

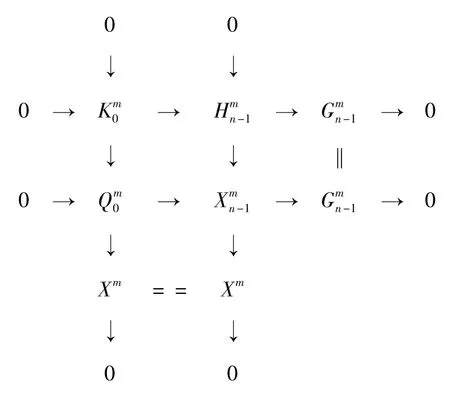
圖6 和的推出圖

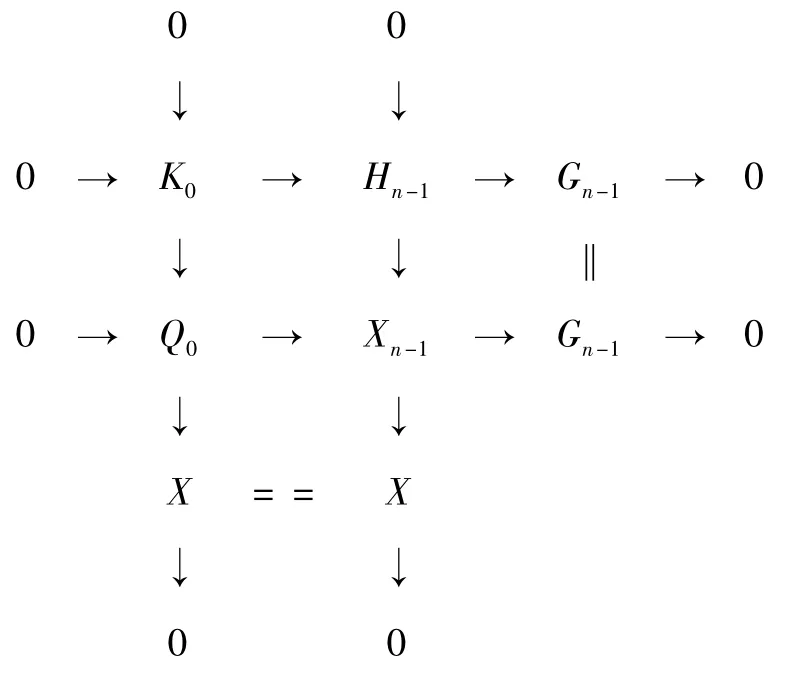
圖7 與圖6 對應的復形交換圖

在正合列0 →Q0→Xn－1→Gn－1→0 中，Q0和Xn－1為C-Gorenstein 投射復形，易知Xn－1為C-Gorenstein 投射復形。對Xn－1用命題1 可知存在復形正合列0 →Xn－1→Q →Xn→0，其中Xn為C-Gorenstein 投射復形，Q 為投射復形。考慮每個層次上的推出圖及對應的復形交換圖分別如圖8 和圖9 所示。

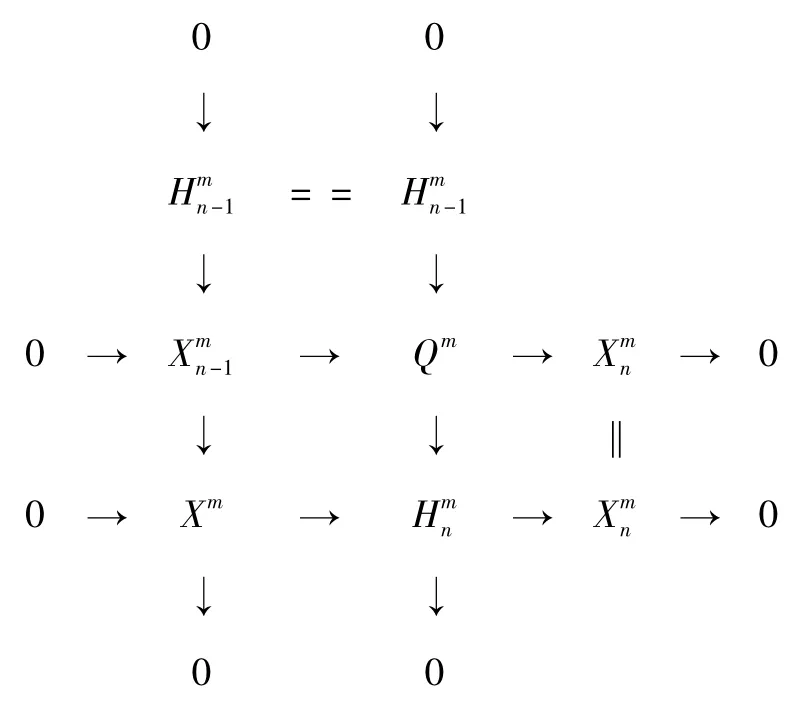
圖8 和的推出圖

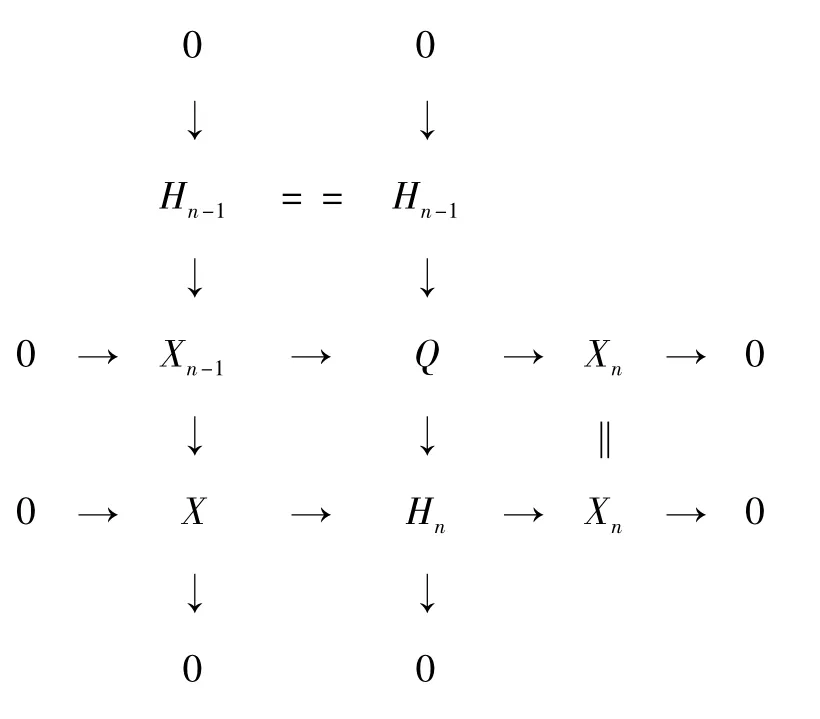
圖9 與圖8 對應的復形交換圖

在正合列0 →Hn－1→Q →Hn→0 中，Q 為投射復形且pd(Hn－1) ≤n －1。可見pd(Hn) ≤n。令G = Xn－1，H = Hn－1，G' = Xn，H' = Hn，則復形正合列0 →Hn－1→Xn－1→X →0 和0 →X →Hn→Xn→0，即為滿足條件的正合列。命題得證。

定理4設X 為左R-模復形，C-Gpd(X) 有限且n為正整數，則以下條件等價:

(1) C-Gpd(X) ≤n;

(2) 對任意投射復形Q，任意i ＞n，有Exti(X，Q)= 0 ;

(3) 對任意投射維數有限的復形Q，任意i ＞n，有Exti(X，Q) = 0 ;

(4) 對任意復形正合列0 →Kn→Xn－1→…→X1→X0→X →0，其中Xi為C-Gorenstein 投射復形，都有Kn是C-Gorenstein 投射復形。

證明顯然成立。

考慮第m 個層次可得Exti(Xm，P) = 0。由文獻［8］中命題3.14 得Gpd(Xm) ≤n，且為C-Gorenstein 投射模。根據定理1，Kn是C-Gorenstein 投射復形。

推論1設X 為左R-模復形，則C-Gpd(X) =存在投射復形Q 使得Exti(X，Q) ≠0} =存在投射維數有限的復形Q 使得Exti(X，Q) ≠0}。

命題2設X 為復形，C-Gpd(X) 有限，則X 有一個特別的C-Gorenstein 投射預覆蓋。

證明因為C-Gpd(X) 有限，由定理4 可知存在復形正合列0 →H →G →X →0，其中G 為C-Gorenstein 投射復形，pd(H) ≤C-Gpd(X) 有限。又因為對任意C-Gorenstein 投射復形C 有從而Hom(C，G) →Hom(C，X) 為滿態射，因此G →X 是一個特別的C-Gorenstein 投射預覆蓋。

3 結束語

利用環模理論和同調代數的方法，研究了復形的C-Gorenstein投射維數的若干性質和等價刻畫。結果表明，復形X 的C-Gorenstein 投射性與其每個層次上的模Xm的C-Gorenstein 投射性密切相關。研究結果補充了Gorenstein 同調代數的基礎理論。