聚焦問題“題眼” 調控解題方向
—— 以一道橢圓三角形面積問題的解題研究為例

吳燕梅

(江蘇省海門中學 226100)

在平時的高中數學教與學中，我們不可避免會引導學生對數學問題進行一系列研究，每個問題都有其考查的意圖.如果抓住問題的要害，即“題眼”，順藤摸瓜，進而對解題方向給出合適的調控，不僅會收獲各種解法，同時會建立不同的思維方式，提升學生圍繞題的本質去探究解題的能力.本文以一道解析幾何問題為例，拋磚引玉.

一、問題呈現

一種畫橢圓的工具如圖1所示．O是滑槽AB的中點，短桿ON可繞O轉動，長桿MN通過N處鉸鏈與ON連接，MN上的栓子D可沿滑槽AB滑動，且DN=ON=1，MN=3．當栓子D在滑槽AB內作往復運動時，帶動N繞O轉動，M處的筆尖畫出的橢圓記為C．以O為原點，AB所在的直線為x軸建立如圖2所示的平面直角坐標系．

(1)求橢圓C的方程；

(2)設動直線l與兩定直線l1:x-2y=0和l2:x+2y=0分別交于P，Q兩點．若直線l總與橢圓C有且只有一個公共點，試探究：△OPQ的面積是否存在最小值？若存在，求出該最小值；若不存在，說明理由．

二、問題分析

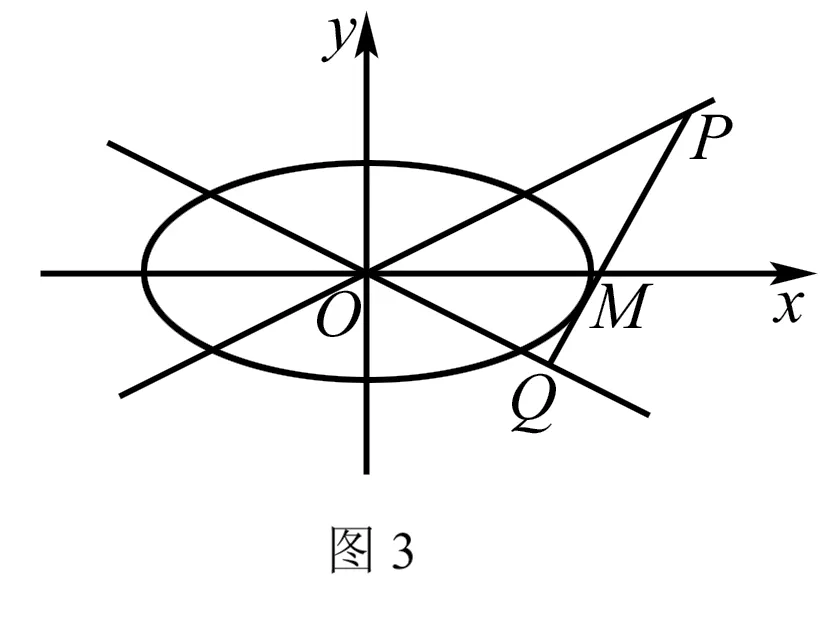
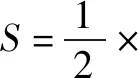
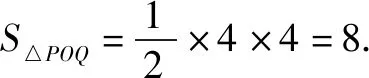
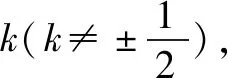
因為直線l與橢圓相切，聯立方程：

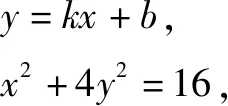
不妨記點P(x1,y1),Q(x2,y2)，

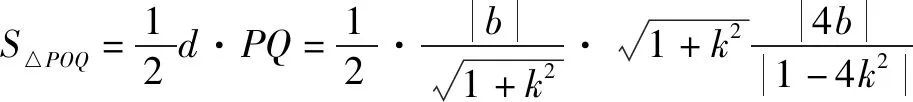
當k=0時，S△POQ=8；

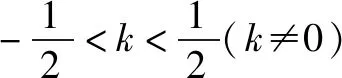
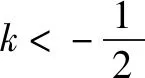
綜上，S△POQ面積最小值為8．

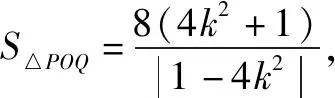
思路2面積割補法

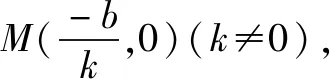
當k=0時，S△POQ=8，故S△POQ面積最小值為8．

點評圖形面積(尤其是不規則圖形)通過分割法轉化為有特殊關系的圖形面積之和，可以簡化計算；這題當中隨直線變化，交點P,Q可能位于x軸同側，所以S△POQ=|S△POM-S△QOM|，結果同法2分析．

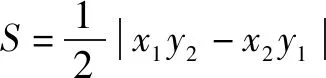
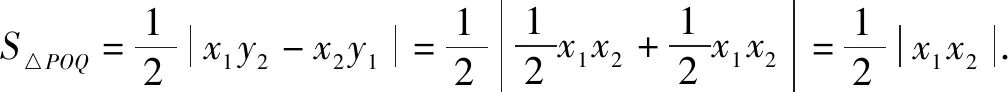
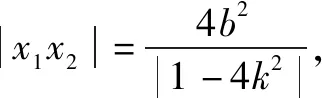
點評這題解法思路，學生是通過平時作業或練習中處理過類似的面積問題，通過聯想遷移，進而構建固定的數學模型，為簡化化簡工作提供了很好的思路．(下面是前期練習中出現的問題(1)，證明可以獨立嘗試多種解法．)

聯想已知橢圓x2+2y2=1，過原點的兩條直線l1和l2分別與橢圓交于A,B和C,D，設△AOC的面積為S．

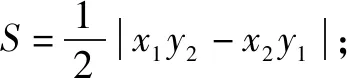
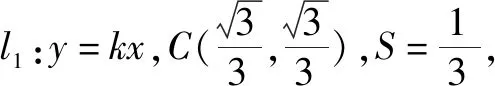
(3)設l1與l2的斜率之積為m，求m的值，使得無論l1與l2如何變動，面積S保持不變．

思路4巧用橢圓切線方程，調控切線表示．

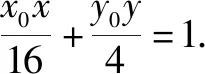
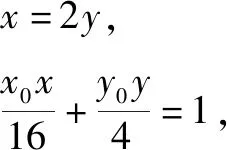
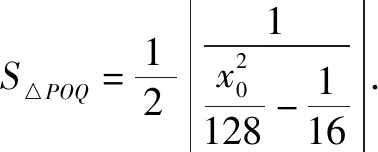
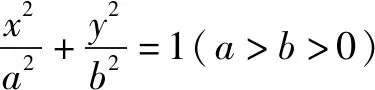
思路5發現定值關系，調控最值計算．

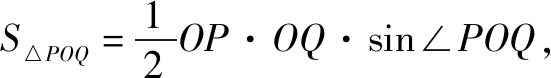
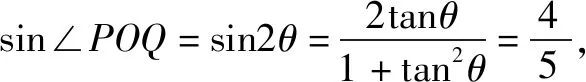
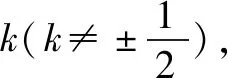
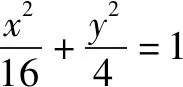
點評解析幾何中涉及最值問題，往往會結合題中條件找到定量關系(定值)，從而為利用基本不等式研究最值創造條件，本題這種解法學生也容易在平時解決的問題中類比聯想找到.