供應商產出隨機與供應中斷下的雙源采購決策

陳崇萍，陳志祥

(1.華南師范大學公共管理學院，廣東 廣州 510006;2.中山大學管理學院,廣東 廣州 510275)

1 引言

制造商在進行物資(原材料或零部件)采購時,常常面臨供應商的兩類不確定風險——產出隨機風險和供應中斷風險。這兩種供應風險都對制造商的正常生產活動產生嚴重的影響。因此研究采購決策中供應商隨機產出和中斷風險對制造商的影響，對指導制造商更好做出科學的采購決策有重要意義。

供應商產出隨機是很常見的，主要是因為生產受到自身條件的限制，如機器故障、工序復雜等，造成供應商有效產量低于計劃產量。這種情況在一些電子元器件與芯片的生產中特別常見。因為這些元器件生產過程相當精密，生產的產品通常在出廠驗貨時才發現大量的產品不合格，導致有效產量極低，如液晶顯示器的平均有效產量通常小于50%[1]。同時，供應中斷的情況也不少見，且一次意外供應中斷就有可能給制造商帶來難以彌補的損失。如2011年3月11日，日本地震導致豐田公司400多種零部件短缺，生產量減少了相當于日常6個多月的產量,損失慘重[2]。再如2004年，生產流感疫苗的生產商凱隆(Chiron)由于其唯一的供應商遭受細菌污染而生產暫停，導致美國產生了嚴重的流感疫苗短缺事件，美國政府不得不控制疫苗的配給，同時很多州疫苗價格暴漲[3]。

為了減輕由于供應產出隨機和供應中斷帶來的損失，同時也為了提高制造商與供應商洽談采購交易合同中的價格談判能力，降低采購成本，大部分的制造商都雙源采購[4]。雙源采購成為制造商應對供應中斷的主要風險管理策略。因為面對概率低的非常規突發事件，雙源采購是最優的[5]。

雙源采購因能有效降低采購風險而被全球的公司廣泛的采用[6]。如世界上最大的工程機械與礦山設備生產商美國卡特彼勒公司就雙源采購，他們向一個低成本公司采購日常需求穩定的材料，同時向另一個快速生產但價格貴的生產商采購緊急需要的材料[7]。研究發現，雙源采購的另外一個優勢是采用兩個供應商能形成競爭，從而為裝配企業獲得更好的采購價格與質量[8]。

本選題基于多年來我們對我國汽車行業調研發現的現實問題。在調研中我們了解到，中國多數汽車企業，如長春一汽，柳州五鈴，武漢神龍、重慶長安、廣汽本田和豐田等，在采購中經常遇到供應商產出隨機和供貨中斷的情況。由于這些大型的汽車裝配商的場地有限，準備的安全庫存也非常有限，遇到供應中斷的情況，只能暫停生產。從制造商處我們了解到，汽車制造商的生產線每停止一分鐘的生產，損失都非常大。同時，遇到這種情況，最快解決也需要一天左右的時間，汽車制造商因此損失慘重。所以汽車制造商不得不采用雙源甚至多源的采購模式，以降低生產被中斷的可能性。同時這些企業的供應商也都經常存在有效產量很不確定的情況，這種情況影響給制造商的有效供貨量從而影響制造商的生產。面對供應商的產出隨機和供應中斷，如何合理確定最優的雙源采購訂貨量，對這些汽車企業有重要意義。

國內外對雙源采購問題進行了不少研究，與本研究有關的主要是產出隨機下的雙源采購和供應中斷下的雙源采購研究。目前國內外研究供應商產出隨機下的雙源采購文獻很多，主要有Tomlin和Wang[9]采用報童模型研究了供應產出不確定情況下最優的雙源采購策略。Zhu[10]研究了兩個供應商具有不同的產出不確定性、生產成本和提前期時最優的雙源采購動態庫存策略。Ju等[11]研究了供應商的產出滿足伯努利分布時最優的雙源采購策略。Jaksic和Fransoo[12]根據提前期長的生產商生產成本提高的新情況，研究了就近生產企業生產能力存在限制情況下的雙源采購問題。Wan和Chen[13]采用期權和現貨市場兩種方式研究了多周期雙源采購供貨問題，研究發現有期權策略比沒有期權時的采購策略要好。

與此同時，對供應中斷風險下的雙源采購問題的相關研究在近幾年也有增加，如Iakovou等[14]研究了兩個供應商都存在供應中斷風險時，制造商雙源采購最優的訂貨策略，但沒有考慮供應商的產出隨機。Sawik[15]研究了在供應中斷的情況下，同時考慮供應商選擇和消費者訂單排序問題時比較了雙源采購和單源采購的優劣。Lücker和Seifert[16]采用庫存、雙源采購和柔性生產能力三種策略保證醫藥供應鏈的可持續性，研究發現當沒有雙源采購策略時，庫存策略和柔性生產能力之間可以替代，但有雙源采購時，雙源采購與柔性生產能力之間就可以替代。Lena和Stefan[17]在供應中斷的情況下，研究了供應商存在學習效應時最優的雙源采購策略。汪傳旭和許長延[18]也考慮了供應中斷情況下，兩個零售商相互轉運的最優策略。在供應中斷和生產成本不確定的情況下，黃河等[19]研究了買方與賣方均可努力改善產出隨機又可降低生產成本的情況下，供應鏈的最優決策。陳崇萍等[20]研究了雙源采購如何質量統一的問題。

現有研究有的將供應中斷和產出隨機簡略的作為同一種風險考慮，有的僅考慮產出隨機或供應中斷。但是，現實中產出隨機和供應中斷風險表現形式和嚴重程度是不同的，刻畫兩類風險的方法和管理策略也不同。產出隨機是一種連續風險，而供應中斷是一種隨機性的風險。因此區別兩類風險在采購決策中的表現，可以更好的分析與應對這兩種風險。本文的貢獻在于，將現實中存在的產出隨機風險和供應中斷風險在雙源采購模型中同時且分開表現，充分考慮到兩種風險的不同表現形式，分析研究了此時雙源采購的最優決策問題，為企業更好的應對這兩種風險提供更好的指導。

2 問題描述、符號說明與基本假設

本文研究的概念模型如圖1所示：假設一個制造商同時向供應商1和供應商2采購同一種零部件。供應商i(i=1,2)沒有出現中斷風險的概率為θi，則出現中斷風險的概率為(1-θi)。供應商1中斷風險可能性低價格高，供應商2中斷風險可能性高價格低，即ω1>ω2，(1-θ1)<(1-θ2)。且每個供應商的產出具有隨機性，即計劃生產量為xi(i=1,2)時，有效產量僅為αixi，其中αi表示產出隨機因子，影響產出隨機因子的主要是供應商的生產條件、技術水平等，αi∈[mi,1]的均勻分布，其概率密度函數與分布函數分別為fαi(αi),Fαi(αi)。

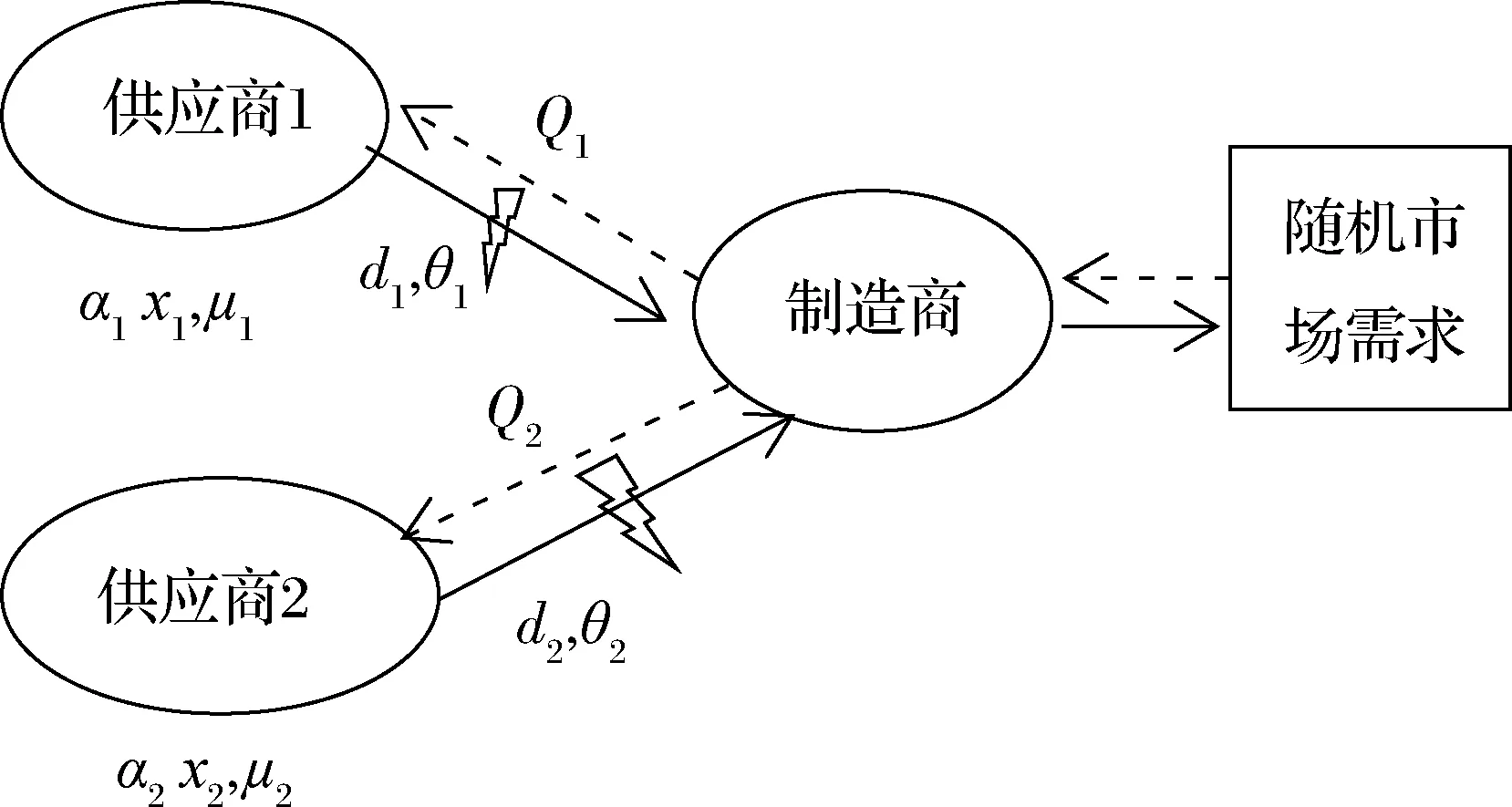
圖1 供應商產出隨機與供應中斷時的雙源采購概念模型

假設最終產品的隨機市場需求用y表示，其概率密度與分布函數分別為fy(y),Fy(y)。最終產品的市場售價為p，未銷售的產品單位殘值為s，單位缺貨損失為ν。且在本文中出現的任何變量，均有n+=max(0,n)。

在下面所有的符號中，我們用下標a表示只考慮供應商產出隨機時的各變量，用下標b表示同時考慮供應商產出隨機與供應中斷時的各變量。

研究中假設制造商與2個供應商均為風險中性的，且信息對稱，決策者完全理性。

3 模型構建

本文分別針對兩種情況建立博弈模型：(1)只考慮供應商產出隨機，(2)同時考慮供應商產出隨機和供應中斷。

3.1 只考慮產出隨機時最優決策

本研究中，制造商是斯坦伯格博弈的領導者，首先決定向兩個供應商的訂貨量，然后兩個供應商再根據制造商的訂貨量決定自身的生產量。這種假設確實與現實情況相符，如很多大型汽車裝配企業，擁有強大的資金與技術實力，零部件供應商跟隨裝配企業的決策而決策。根據決策的先后順序，我們采用反向求解的方法，即首先求解供應商的最優生產量，然后求解制造商的最優訂貨量。

3.1.1 供應商最優生產量

在制造商給定的價格ωi下，供應商的計劃產量為xia(i=1,2)時，供應商i(i=1,2)給制造商的供貨量為dia(dia=min(Qia,αixia)，此時供應商i的利潤函數為：πia=ωidia-cixia

因此供應商的期望利潤為：

Πia=ωiE(dia)-cixia

(1)

可知供應商最優的生產量滿足如下條件(證明詳見附錄I)：

(2)

3.1.2 制造商最優的訂貨量

假設此時制造商向供應商i的訂貨量為Qia，有dia(dia=min(Qia,αixia)。以下都有：當i=1時j=2;當j=1時，i=2。制造商利潤函數用πa表示為：

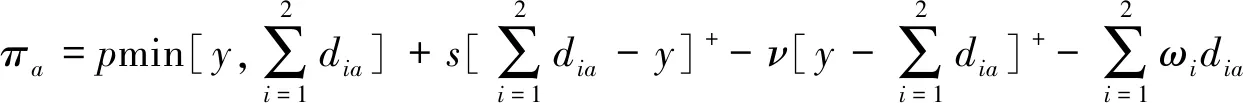
(3)

制造商此時的期望利潤用Πa表示為：

其中的Aa,Ba,Ca詳見附錄II。

定理1只考慮供應商產出隨機時，存在唯一向兩個供應商的最優訂貨量使得裝配企業利潤最優。

證明:對制造商期望利潤函數(3)式求向供應商i的訂貨量Qia的一階導數為：

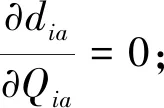
(5)

對(5)式求訂貨量Qia的二階導數得：

+min(Qja,αjxja)]+(p+ν)-ωi]

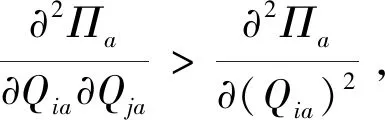
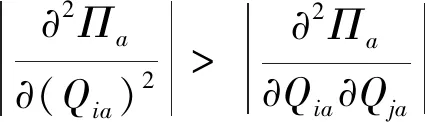
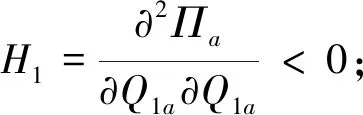
由以上證明可知，海塞矩陣是負定的，也就是以上函數存在唯一最大值，證畢。

-(p-s+ν)E[Fy(Qia+dja)]+(p+ν)-ωi=0

(6)

因為每個供應商的生產量是根據制造商的訂貨量而決策的量，且因為存在生產擾動性，使得供應商的生產量不可能一直等于訂貨量，所以：

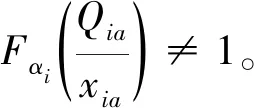
(7)

在以上的等式中，左邊的銷售價格p，單位缺貨損失ν，單位殘值s和采購價格ωi均是常數。

3.2 供應商產出隨機和供應中斷時最優決策

3.2.1 供應商最優生產量

類似3.1節的求解過程，我們首先求解供應商存在產出隨機與供應中斷可能性時最優的生產量。

在制造商給定的價格ωi下，供應商i(i=1,2)的計劃產量為xib(i=1,2)時，供應商i給制造商的供貨數量為dib(dib=θimin(Qib,αixib)，此時供應商i的利潤函數用πib表示為：

πib=ωidib-cixib

此時供應商的期望利潤用Πib表示為：

Πib=ωiE(dib)-cixib

(8)

可知供應商最優的生產量滿足如下條件(證明與附錄I類似，此處省略)。

(9)

3.2.2 制造商最優訂貨量

此時制造商每次可接收到供應商的供貨量為：

制造商此時的利潤函數用πb表示為:

因為：

-[y-db]+=-max[y-db,0]=(db-y)-(db-y)+

所以有：

min[y,db]=-max(-y,-db)]=db-max(db-y,0)=db-(v-y)+

以上利潤函數可化簡為：

(10)

制造商的期望利潤函數用Πb表示為：

制造商此時的期望利潤函數Πb也可表示為：

Πb=-(p-s+ν)Ab+(p+ν)Bb-νE(y)-Cb

(11)

其中的Ab,Bb,Cb詳見附錄Ⅲ。

定理2考慮供應商產出隨機和供應中斷時，存在唯一向兩個供應商的訂貨量，使得制造商的利潤最優。

證明:對制造商利潤函數求向供應商i訂貨量Qib的一階導數為：

類似3.1.2節有：

+ν)E[Fy(θiQib+djb)]+(p+ν)-ωi]

(12)

+ν)E[Fy(θiQib+djb)]+(p+ν)-ωi]

因:

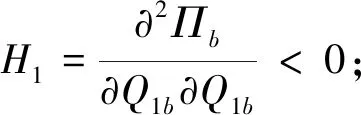
由以上證明可知，海塞矩陣負定，以上函數存在唯一最優解，也就是制造商存在唯一最優的向兩個供應商的訂貨量使得自身利潤最大，證畢。

最優的條件為：

(13)

4 算例與管理啟示

4.1 最優決策與最優利潤

假設一個制造商同時向兩個供應商采購相同的關鍵零部件，制造商向兩個供應商的采購價格分別為ω1=53,ω2=50，兩個供應商的生產成本分別為c1=23,c2=20；兩個供應商沒有發生供應中斷的概率為θ1=0.95，θ2=0.90;兩個供應商均存在一定的生產不確定性，供應商i(i=1,2)的產出隨機性因子αi滿足[mi,1]上的均勻分布，則概率密度函數為fαi(αi)=1/(1-mi)。隨機市場需求y∈[200,300]上的均勻分布，最終產品的市場銷售價格p=150，未銷售的產品單位價格s=70，每單位缺貨損失ν=50。

由圖2可知，制造商的利潤關于兩個供應商的訂貨量的圖像有一個上凸的趨勢，說明存在最優值，最優值在圖像的最頂點處。

圖2 兩個訂貨量對造商利潤的影響

以下我們分別求解兩種情況下供應商最優的生產量，制造商最優的訂貨量。求解過程是：將以上基本參數代入各式，聯立(2)與(7)式可解得:只考慮供應商產出隨機時供應商最優的生產量(x1a,x2a)，制造商最優的訂貨量(Q1a,Q2a)，再將最優訂貨量和最優生產量代入(4)式和(11)式中可解得：制造商此時最優的期望利潤(Πa)和兩供應商最優的期望利潤(Πia)；聯立(9)與(13)式可解得:在同時考慮供應商產出隨機和供應中斷時供應商最優的生產量(x1a,x2a)，制造商最優的訂貨量(Q1b,Q2b)，然后將它們代入(11)和(8)式中可解得:制造商此時最優的期望利潤(Πb)和供應商最優的期望利潤(Πib)。且我們在求解中發現，確實只有一組非零解，與定理1和2的證明一致。

只考慮供應商產出隨機與同時考慮供應商產出隨機與供應中斷時，供應商最優生產量與制造商最優訂貨量和最優利潤，如表1所示。

表1 兩種情況下的最優解

從表1中我們可以看出：考慮供應中斷的情況下，制造商最優的訂貨量與供應商最優的生產量均比沒有考慮供應中斷時大，即x1aΠb。以上分析顯示，考慮供應中斷時，制造商應該多訂貨;同時供應商也應該多生產。

4.2 靈敏度分析

以下分析供應商產出隨機性與供應中斷可能性對最優決策的影響。

4.2.1 產出隨機對最優值的影響

供應商的產出隨機性不僅會對自身的決策造成影響，還會對制造商的決策與利潤造成影響。以下將分析供應商產出隨機變化對最優決策與最優利潤的影響。由以上的分析可知，隨著mi的增大，供應商i產出更穩定，有效產出更高。

按4.1節的計算過程，在只考慮供應商產出隨機時，我們先增大m1的值，也就是讓供應商1的產出更穩定，有效產量更高;然后增大m2的值，也就是讓供應商2的產量更穩定，有效產出更高。可得各最優值如表2所示。從表2中可以看出：

表2 供應商產出隨機率對最優值的影響

(1)隨著mi的增大，供應商i的生產量先增加，直到產出穩定改善(隨機性降低)到一定程度(如mi=0.9)時，供應商i的生產量才減少。

(2)隨著mi的增大，制造商向供應商i的訂貨量一直增加，向供應商j的訂貨量一直減少。同時發現當mi增大到一定程度時，制造商向供應商j的訂貨量幾乎為零(如m1=0.9，Q2a=13.13;m2=0.9時，Q1a=1.78所示)。也就是說，當其中一個供應商產出穩定性改善到一定程度時，不再向另一個供應商訂貨，意味著另一供應商將會被淘汰。

(3)隨著mi的增大，供應商i的最優期望利潤在增加，供應商j的最優期望利潤在減小，但制造商的最優期望利潤一直在增加。

以上結論顯示，供應商產出穩定性改善到一定程度時，供應商才會減少自身的生產量，在那之前，供應商在改善自身產出穩定性，降低產出隨機性的同時還應該增加生產量。同時，制造商應該向不斷改善產出穩定性的供應商多訂貨，逐漸減小未改善產出穩定性供應商的訂貨量，最終幾乎全部向一直改善產出穩定性的供應商訂貨。此現象也說明，制造商在供應商產出隨機時采用雙源采購是為了降低風險，當風險足夠低的時候，也就是其中一個供應商的產出穩定性改善到一定程度時，雙源采購會被單源采購所取代。同時制造商與供應商應該合作改善供應商的產出穩定性，降低產出隨機性，因為供應商產出穩定性的改善，不僅提高供應商利潤，也提高制造商利潤。

在供應商存在產出隨機和供應中斷時，同樣改變兩個供應商的產出隨機性。按4.1節的求法，可得表3。

由表3可知，同時考慮兩個供應商存在產出隨機與供應中斷時的各個最優決策和最優利潤，與只考慮存在產出隨機時的情況相同，此處的分析省略。

4.2.2 供應中斷可能性對最優值的影響

以上分析了產出隨機對最優值的影響，接著我們將分析供應中斷可能性對最優值的影響。依次改變供應商i供應中斷的可能性，隨著θi的增大，供應商i的供應中斷可能性降低。也按照4.1節的計算過程，代入各式可得表4。從表4中我們可以清楚的看到：

(1)無論雙源采購中哪個供應商的供應中斷可能性降低，制造商向兩個供應商的最優訂貨量都在減小，但制造商的最優期望利潤一直在增加。

(2)無論雙源采購中哪個供應商供應中斷可能性降低，兩個供應商的最優生產量都在減小，供應商i的利潤隨供應商i供應中斷可能性的降低而增加，隨供應商j供應中斷可能性的降低而減小。

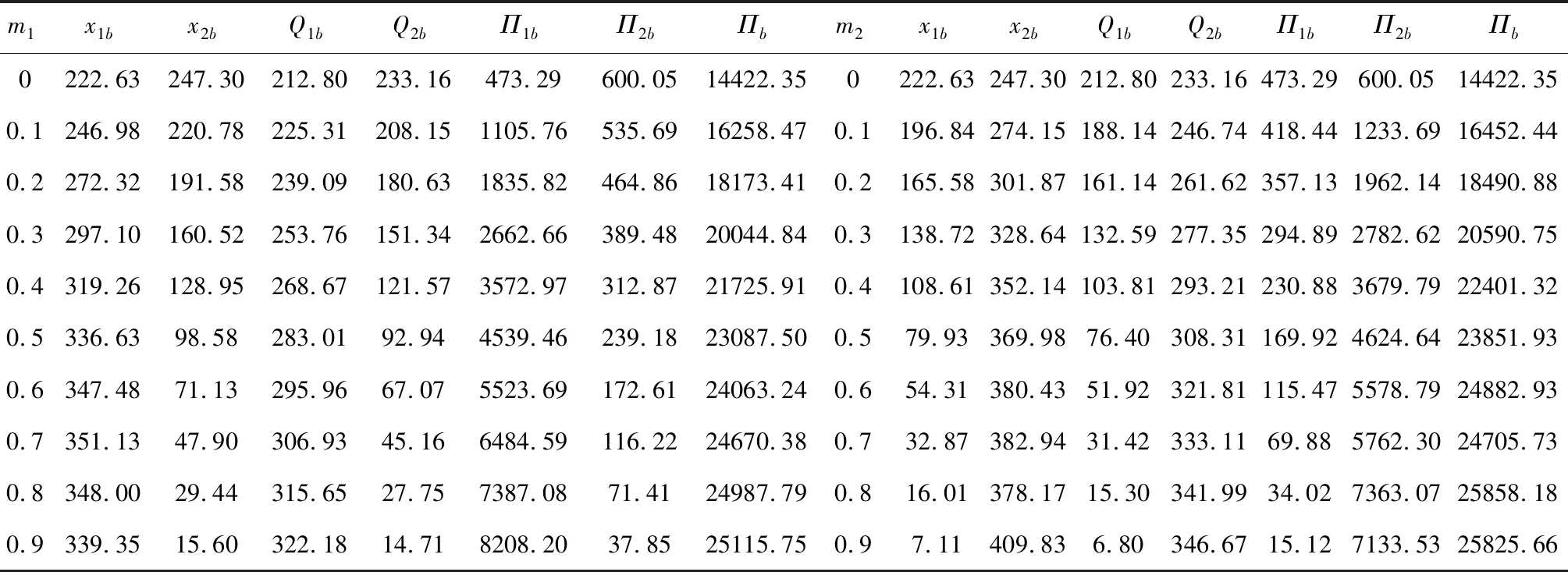
表3 風險中斷時供應商產出隨機率對最優值的影響

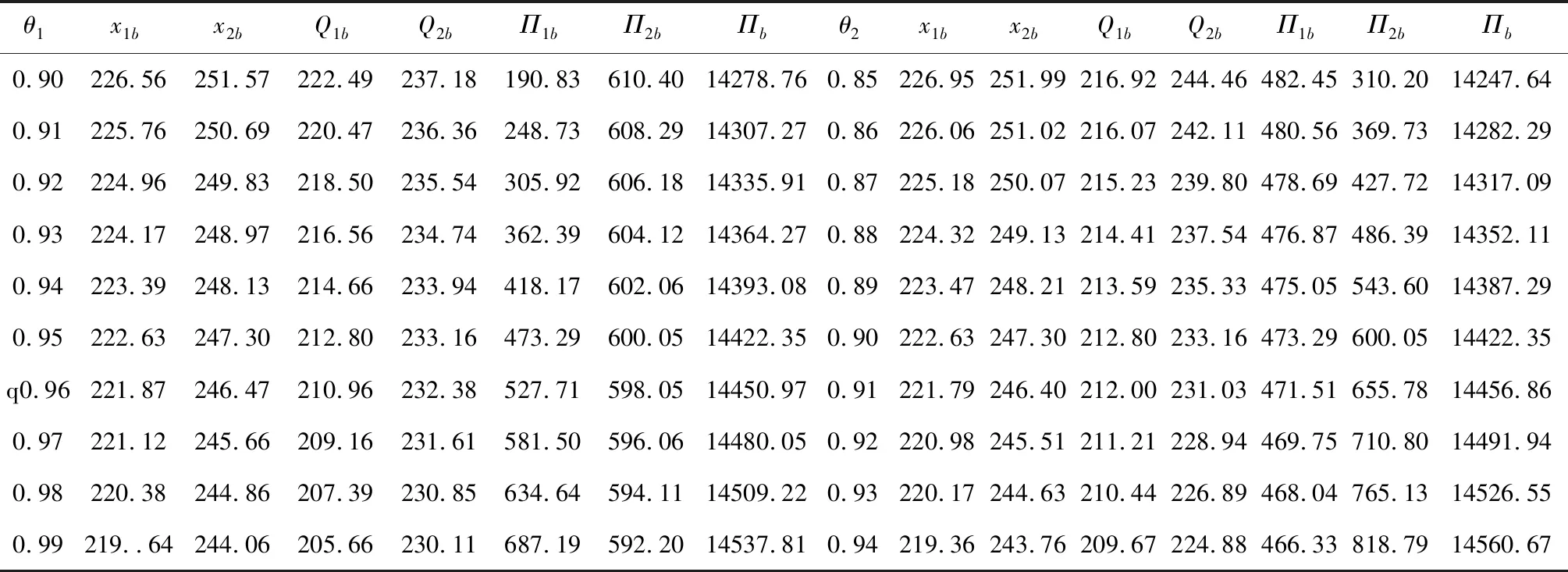
表4 供應中斷可能性對最優值的影響

4.3 管理啟示

由本文的理論模型和算例分析可知，供應商的產出隨機不僅與供應商密切相關，還影響著制造商的利潤與決策。因此在現實中，制造商在做采購決策時應該考慮這種供應不確定性對采購的影響，并準備應對措施。比如，在供應商產出率不穩定時采用雙源采購，并督促供應商降低自己的產出隨機性，一旦其中有供應商產出率穩定性得到很大的改善(產出隨機性降低)，改善到一定程度時，制造商可以采用單源采購的形式，這也是準時化JIT采購的要求。對供應商來說，在給制造商供貨的同時，應該在制造商的幫助下努力改善自己的生產與供應條件。

同時可知，在雙源采購決策中，任何一個供應商供應中斷概率的降低都可以增加制造商的利潤水平，因此制造商在選擇供應商時，應該將供應商供貨中斷風險作為一個重要考核因素，同時，還應該時刻關注供應商供應中斷的原因，力求降低供應商供應中斷的可能性。

5 結語

本文研究供應商隨機產出和中斷兩種風險下制造商采購與供應商的生產最優決策。論文推導出只考慮供應商產出隨機和同時考慮供應商產出隨機與供應中斷可能性時，制造商與供應商的最優決策與利潤。研究發現：

(1)雙源采購中,同時考慮供應商產出隨機與供應中斷風險時，制造商與供應商利潤均比只考慮制造商產出隨機時低，而制造商的最優訂貨量與供應商的最優生產量均比只考慮供應商產出隨機時高。

(2)雙源采購中，制造商的最優期望利潤均隨著任一供應商產出隨機性降低而增加;制造商的最優訂貨量隨著供應商自身的產出隨機性降低而增加。

(3)在雙源采購中，其中任何一個供應商最優期望利潤隨著自身產出隨機性降低而增加，隨著另一個供應商產出隨機性降低而減少;供應商最優生產量隨著自身產出隨機性降低先增后減，隨著另一個供應商產出隨機性降低而減少。

(4)雙源采購中,任何一家供應商供應中斷概率降低，都會導致制造商向兩個供應商的訂貨量都減小，制造商的最優利潤都增加;同時,供應商的最優生產量都減小。

(5)在雙源采購中,供應商最優利潤隨自身供應中斷概率降低而增加，隨著另一家供應商供應中斷概率的降低而減小。

以上研究表明，制造商采用雙源采購是應對供應隨機和中斷風險下的暫時策略，在風險足夠低的情況下，制造商可以采用單源采購。同時供應商需要不斷改善自身的供應條件，否則會被淘汰。

未來可在本研究的基礎上做多方面的擴展，比如研究供應商存在生產規模限制條件下的雙源采購問題；研究多級供應情況下的雙源采購問題等。

附錄：

附錄Ⅰ：對供應商的期望利潤函數Πia求一階二階導數可得：

因為二階導數小于零,可知當一階導數為零時,以上期望利潤存在唯一最大值，條件為：

附錄Ⅱ：

fα1(α1)dα1fα2(α2)dα2

+Q2a)fα1(α1)dα1fα2(α2)dα2

附錄Ⅲ：

-y)fy(y)dyfα1(α1)dα1fα2(α2)dα2Bb=E[db]