依標靠綱明確主題,由易到難預設小結
——以中考“軸對稱圖形”復習為例
☉江蘇省海門市能仁中學 陸新鋒
最近學校備課組打磨中考“軸對稱圖形”復習內容時,從最初的只涉及軸對稱相關綜合題的選題方向調整為基于“課標”“考綱”而選題備課,組內同事對這節課的教學目標、主線與選題都有了更深的理解.本文整理該課的教學設計,并跟進教學立意的闡釋,供研討.
一、中考“軸對稱圖形”復習課教學設計
活動1:觀察一組圖形
觀察以下4個圖形(如圖1):
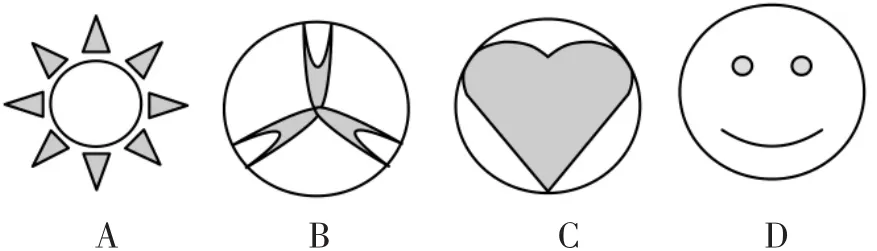
請說說這組圖形有怎樣的共同點.
預設:學生識別出這組圖形都是軸對稱圖形,引出本課的課題,教師板書本課課題“軸對稱圖形”.
活動2:研究常見幾何圖形
例1觀察以下3個圖形(如圖2):

圖2
(1)這3個圖形中有軸對稱圖形嗎?如果有,你能作出它們的對稱軸嗎?
預設:提醒學生是“作出對稱軸”,需要尺規作圖,由學生上臺講解或演示作法即可.
接著給出如下追問:
(2)你還熟悉哪些特殊的等腰三角形?它們的對稱軸有幾條?
預設:比如,等邊三角形有3條對稱軸,等腰直角三角形只有1條對稱軸,等等,這里不深究,學生答出一種以上即可,主要是為了過渡引出特殊的平行四邊形.
(3)平行四邊形家族中有沒有軸對稱圖形呢?舉例說說.
預設:有.比如,矩形、菱形、正方形.請畫一畫它們的對稱軸.
(4)前面提到了等邊三角形、正方形、圓,是否可以猜想:所有正多邊形都是軸對稱圖形?如果是,研究一下它們對稱軸的條數.
預設:所有正多邊形都是軸對稱圖形,正多邊形都是軸對稱圖形,它的對稱軸條數與邊數相等.
練習1:如圖3,比較正五邊形與正六邊形,可以發現它們的相同點與不同點.請你寫出它們的兩個相同點和兩個不同點.
預設:學生可以從多邊形的邊、角、對角線、內角和、外角和、軸對稱性質、對稱軸條數等角度分析它們的相同點和不同點.這是一個開放式問題,教學時注意安排不同的學生回答,但不需要太多解答,重要的是讓學生知道研究正多邊形可以從哪些角度或元素入手.
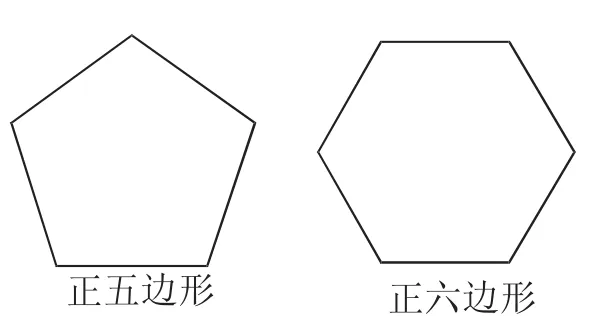
圖3
活動3:繼續探索幾種特殊幾何圖形的軸對稱性質
例2觀察一幅三角尺(如圖4):
(1)請將它們分別補成一個正多邊形;
(2)等邊三角形的3條對稱軸交于一點嗎?為什么?
(3)如圖5,設補成的正方形ABCD的邊長為4,點M在邊CD上,M、N兩點關于對角線AC對稱.若DM=1,你能設計一個怎樣的問題?
練習2:如圖5,正方形ABCD的邊長為4,點M在邊DC上,M、N兩點關于對角線AC對稱,若DM=1,則tan∠ADN= .
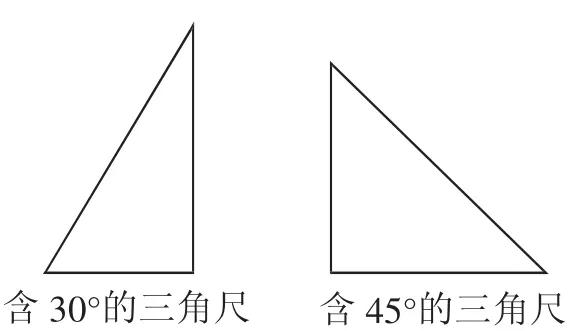
圖4

圖5
活動4:較難題中常見“軸對稱”身影
例3如圖6,矩形ABCD中,E是AB的中點,將△BCE沿CE翻折,點B落在點F處.
(1)判斷△ABF的形狀,并說明理由.
(2)找出圖中與△AEF相似的三角形.
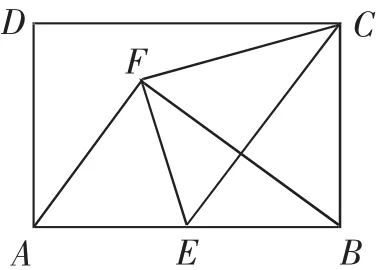
圖6
預設:學生獨立練習,然后講評,突出軸對稱性質在思路貫通中的作用,再出示一道同類練習(限于篇幅,略去).
活動5:課堂小結
小結問題1:本課主要復習的是軸對稱圖形,你一般怎樣快速判斷一個圖形是否為軸對稱圖形?
小結問題2:在軸對稱的兩個圖形中,對應點的連線段與對稱軸有怎樣的位置關系?
小結問題3:畫出一個三角形關于某條直線對稱的三角形時,你會怎樣操作?舉例說說.
附板書設計:中考一輪復習“軸對稱圖形”.

二、教學立意的進一步闡釋
1.依標靠綱,準確定位復習目標和選題主線
中考復習應對的是各地中考試卷,而中考命題的依據除了課本,主要是國家層面的課程標準(即“課標”)和本地區發布的“考綱”(有些地區稱之為“考試說明”),國家層面的“課標”因為內容不多,在我們具體備課時往往能找到的內容表述有限,這時還要結合本地區發布的“考綱”進行研習,分析某個知識點或知識模塊在本地區“考綱”中有怎樣的表述或對一些具體的知識或技能有哪些明確的能力層級的要求.比如,上文關注的“軸對稱圖形”課例,整合“課標”與本地區“考綱”后,發現有一些具體的要求,比如,了解軸對稱的概念、軸對稱圖形的概念(只需要達到了解層級),能在自然界或現實圖形中識別軸對稱圖形;理解軸對稱的基本性質,成軸對稱的兩個圖形中,對應點的連線被對稱軸垂直平分;會探索等腰三角形、矩形、菱形、正多邊形、圓的軸對稱性質(這些技能需要達到理解層級);能畫出簡單平面圖形(點、線段、直線、三角形等)關于給定對稱軸的對稱圖形(這個技能需要達到掌握的能力層級).可以發現,這也就是上文課例的復習目標與選題主線.
2.由易到難,從概念梳理復習再到難題講評
在明確復習目標與選題主線之后,我們需要精心設計和呈現各個不同教學環節,首先要堅持由易到難的選編原則.軸對稱圖形的復習課例中,我們先通過學生熟悉的一些軸對稱圖形復習核心概念,并圍繞與之相關的一些概念梳理出知識結構,輔以簡單的小題及變式練習進行鞏固訓練,再逐漸過渡到較難習題,并安排學生獨立思考后再開展互動式講評.值得注意的是,發給學生的活動單(或者導學案)要注意留白式呈現,不宜把一些例題的多個設問都印制在活動單上,而是只對一些例題或問題給出一兩個簡單的設問,將有些漸次生成的后續設問以PPT方式在上課時陸續給出,因為課堂是動態變化的,有時還要結合學情進行增刪取舍.我們有時見到老師們手捧一份密不透風的習題單導學案,一題接一題高密度地講授、灌輸,匆忙下課之后,老師把大容量的導學案“講完”,但是學生接受多少?學生的思維是否最大化參與課堂中的一些問題呢?恐怕要大打折扣吧.
3.注重小結,預設小結問題及時反饋學情
中考復習往往由于習題講評的任務多,常常出現“拖堂”現象,課堂小結也容易被擠占,這也算是一種“教學遺憾”.我們認為,在備課階段就要充分預留課堂小結時間,并預設出“獨特的”小結問題.比如,上文課例在小結階段,我們針對本課前面所復習或講評的典型問題設計的系列問題,既帶領學生進行課堂復習小結,同時呼應了本課復習目標與“考綱”要求,當然也是一種反饋學情式的小結問題.
三、寫在后面
本文提供的課例并沒有涉及圖形與坐標的內容,是因為“課標”上另有“圖形與坐標”的模塊,故沒有涉及.這與有些復習資料上“混為一課”不太相同,作為文末,故做說明,以為明辨.

