雙平行導線間軸向運動導電梁的動力穩定性

胡宇達，張立保，劉 鄭，張明冉

(1.燕山大學 建筑工程與力學學院，河北 秦皇島 066004；2.燕山大學 河北省重型裝備與大型結構力學可靠性重點實驗室，河北 秦皇島 066004；3.河北醫科大學 后勤管理處，河北 石家莊 050017)

0 引言

在現代工程領域中，存在許多軸向運動結構，如運動導線、板帶軋制、電磁運輸器件等。當運動結構件處于復雜場環境中時，系統將出現耦合振動及穩定性等問題，并影響著結構的正常運行，而這些問題的研究也具有理論和實際意義。Pellican[1]研究了軸向運動系統的振動特性，分析了復雜系統動態響應的實驗和數值計算結果；Chen等[2-4]應用伽遼金法對軸向運動梁的固有頻率以及對軸向運動粘彈性梁的參數振動等問題進行了研究，分析了系統的穩定性；陳樹輝等[5-6]應用L-P法對軸向運動梁的非線性內共振問題進行了研究；Ghayesh等[7]研究了軸向運動Timoshenko梁固有振動問題的分析方法；Wang等[8]研究了軸向運動梁的模態頻率特性。對于磁場環境中運動結構模型的研究，Hu等[9-10]建立了磁場中軸向運動導電薄板的磁彈性耦合振動方程，研究了系統的非線性共振及動力穩定性問題，并對磁場中軸向變速運動薄板的主參數共振問題進行了研究，此外，胡宇達等[11-12]針對磁場環境中軸向運動導電導磁梁磁彈性耦合振動的理論建模問題進行研究，推導出了導電導磁梁的磁彈性振動微分方程，并且分析了軸向運動載流梁在簡諧激勵作用下的磁彈性強迫振動問題；Nayak和Thompson等[13-14]研究了磁流變彈性體夾層梁的振動和混沌動力學等問題；Hasanyan等[15]研究了載流磁彈性平板的屈曲問題。從已有文獻看，針對軸向運動結構或結構磁彈性問題的研究比較深入，但研究軸向運動梁的磁彈性振動問題的相關文獻還很少。本文在筆者所建理論模型基礎上，進一步考慮了平行導線產生磁場的作用，針對平行導線產生磁場區域軸向運動梁的動力穩定性問題進行分析，討論奇點類型；因考慮了梁的橫向振動位移對磁場分布的影響，所以電磁力中體現了彈性振動位移與導線電流間的耦合效應。

1 雙平行導線間軸向運動梁的磁彈性方程

研究雙載流平行導線間同面內的軸向運動導電梁，如圖1所示建立直角坐標系。該梁沿著x軸方向以速度c做軸向運動，并且受到兩端軸向拉力F0x作用，梁長為l，高為h，寬為b，導線通入的電流分別為I1和I2，導線與梁間的距離分別為d1和d2。

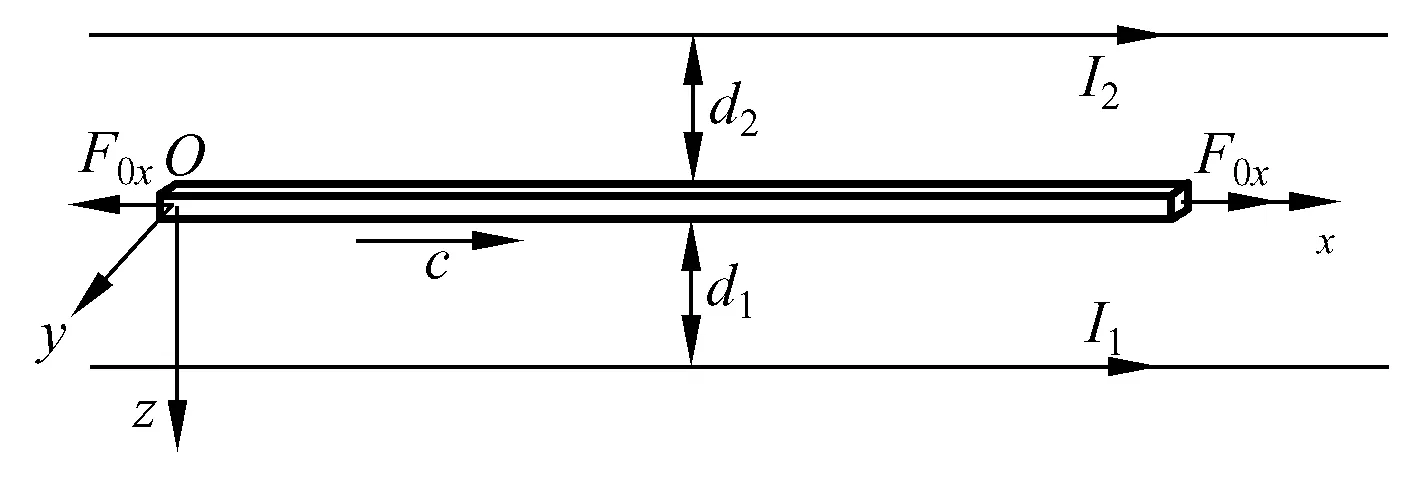
圖1 雙導線間軸向運動梁模型
Fig.1 Axially moving beam model between two parallel wires

1.1 動能和勢能

當軸向運動梁產生橫向振動時，系統的動能表達式為[11]

(1)

式中，ρ為質量密度；A=hb為截面面積；w(x,t)為梁的橫向位移；t為時間變量。

梁的勢能包括梁的彎曲應變能和軸向拉力F0x引起的應變能，其總勢能為

(2)

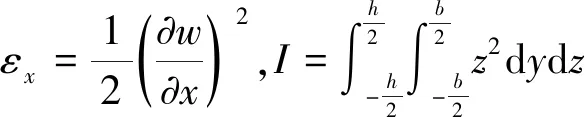
1.2 電磁力

根據電磁場理論，通電導線周圍將產生感應磁場，彈性梁運動時所在位置產生的作用磁場矢量為

(3)

式中，μ0為真空磁導率，j為沿y方向的坐標單位向量；當通入的電流I1與I2同向時取“-”號，反向時取“+”號(下同)。進一步可得運動梁體內沿軸向的感應電流密度為

(4)

這樣，依據電動力學理論，可推得軸向運動導電彈性梁所受單位長度電磁力為

(5)

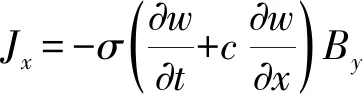
1.3 磁彈性方程

根據上面給出的表達式，基于哈密頓變分原理，可推得雙平行導線間軸向運動導電梁的磁彈性振動方程：

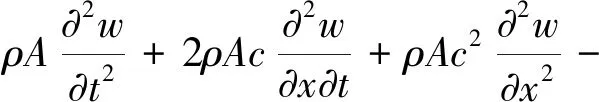
(6)

將式(6)的右端進行Taylor級數展開，略去三次方以上的高階項后可進一步得到系統的非線性振動控制方程：

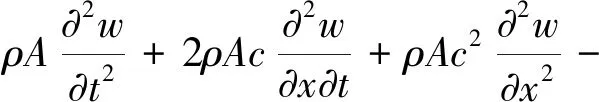
(7)

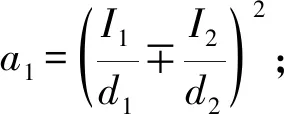
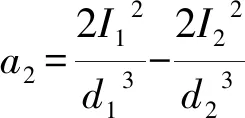
當研究軸向運動梁兩端具有鉸支約束情況時，可將滿足邊界條件的位移解取為下面分離變量展開形式為

(8)

將式(8)代入式(7)中，進行伽遼金積分運算，可得關于時間變量的振動微分方程：

(9)

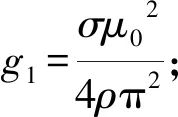
2 奇點穩定性分析

下面應用奇點理論對動力系統(9)的穩定性問題進行分析。首先將式(9)轉化為一階狀態方程形式：

(10)

式中，x=q(t)。

由式(10)可見，非線性系統有唯一奇點(0,0)。因系統(10)雅柯比矩陣是非奇異的，因此依據李雅普諾夫穩定性理論可知，其與如下線性近似系統具有相同的奇點類型：

(11)

根據判別式Δ=p2-4q(這里，p=-g1a1，q=k)，可得下面劃分奇點及其穩定性的條件：

1)Δ≥0時,當q>0，奇點為穩定結點；當q<0，奇點為不穩定鞍點；

2)Δ<0時,此時需滿足q>0，奇點為穩定焦點。

3 數值算例

針對雙平行同向導線間軸向運動鋁制材料梁動力學穩定性進行計算分析，主要參數：密度ρ=2 670 kg/m3，電導率σ=3.63×107(Ω·m)-1，真空磁導率μ0=4π×10-7H/m，彈性模量E=71 GPa，梁長l=1 m。

根據奇點分析判別式進行求解，圖2～4得到了奇點的類型及其穩定性劃分區域。

圖2(a)為判別式Δ=0時的速度-電流臨界曲面圖，圖2(b)和圖2(c)為對應圖2(a)的穩定性平面截圖(取d1=0.05 m，d2=0.05 m)。由圖2(b)可知，隨電流I1的增大，臨界速度由1個變為2個，奇點類型也由2個變為3個，此時由穩定焦點轉化為穩定結點所需的速度c逐漸減小，而奇點變為鞍點的臨界速度為不變值。由圖2(c)可知，隨電流I2的逐漸增大，奇點由穩定焦點轉化為穩定結點所需的速度c先增大后減小，中間出現由穩定焦點轉化為鞍點的不變臨界值情況，且穩定結點的區域相對較小，速度對系統穩定性的影響非常敏感。

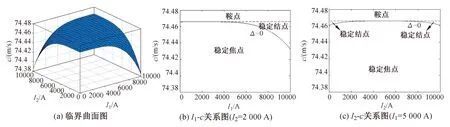
圖2 速度-電流穩定性圖
Fig.2 Velocity-current stability diagram

圖3(a)為判別式Δ=0時的速度-距離臨界曲面圖，圖3(b)和圖3(c)為對應圖3(a)的穩定性平面截圖(取I1=5 000 A，I2=2 000 A)。由圖3(b)可知，隨距離d1增大，奇點由穩定焦點轉化為穩定結點所需的速度也逐漸增大，且達到一定值后穩定結點消失，之后退化為由穩定焦點直接轉化為鞍點的單臨界速度情況。由圖3(c)可知，隨距離d2的增大，奇點由穩定焦點轉化為穩定結點所需的速度c先增大后減小，中間出現由穩定焦點直接轉化為鞍點的單臨界速度情況。

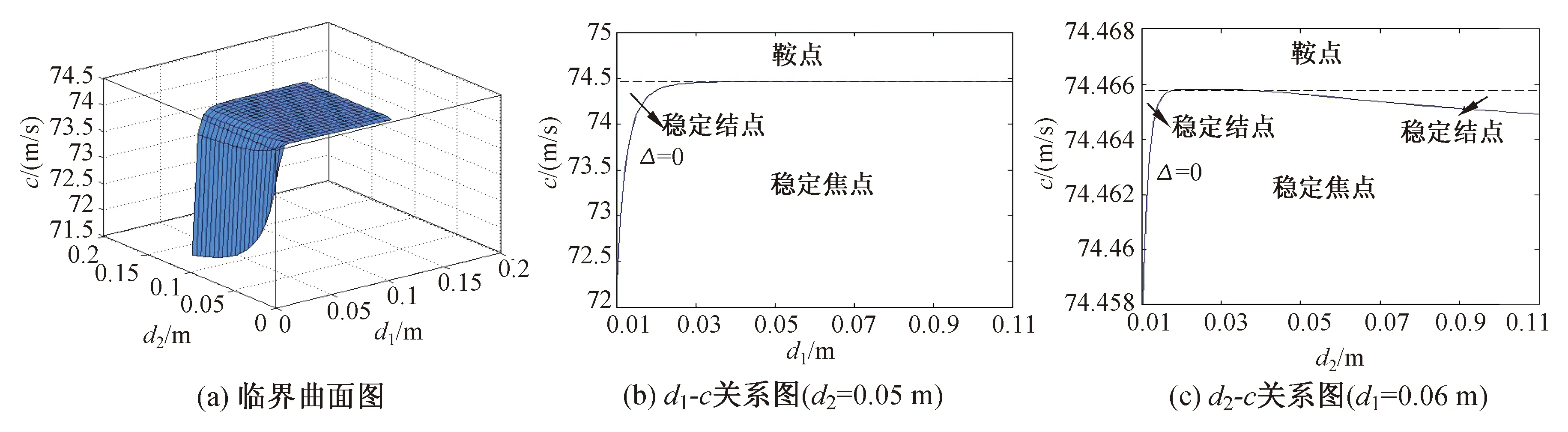
圖3 速度-距離穩定性圖
Fig.3 Velocity-distance stability diagram

圖4(a)為判別式Δ=0時的電流-距離臨界曲面圖，圖4(b)和圖4(c)為對應圖4(a)的穩定性平面截圖。由圖4(b)可知，在給出的參數范圍內，存在穩定焦點和穩定結點兩個區域，且隨距離d1的增大，由穩定焦點轉化為穩定結點的臨界電流也逐漸增大。由圖4(c)可知，臨界電流仍為單值，且隨距離d2的增大，奇點由穩定焦點轉化為穩定結點所需的電流值I1逐漸變小。

圖4 電流-距離穩定性圖
Fig.4 Current-distance stability diagram

4 結論

本文推導出了兩根導線產生磁場環境中軸向運動導電梁的磁彈性振動方程，對系統奇點穩定性問題進行了分析，給出了穩定性判別條件，計算結果表明：

1)在速度-電流和速度-距離穩定域中，存在穩定焦點、結點和不穩定鞍點的三個區域，對應的也存在兩個臨界速度值情況，且系統的穩定性依賴于軸向速度非常敏感。

2)在電流-速度穩定域中，僅存在穩定焦點和穩定結點兩個區域，沒有鞍點區域，對應的臨界速度為單值。可見，通過相關參數的控制，能夠使系統達到穩定運動狀態區域，所得結果可為工程實際提供理論參考。