習(xí)題變式在初中幾何教學(xué)中的應(yīng)用研究

王曉強(qiáng)

[摘? 要] 變式教學(xué)，是一種教師以一道典型的習(xí)題為基礎(chǔ)，通過變化習(xí)題來引導(dǎo)學(xué)生逐步拓展知識(shí)、培養(yǎng)思維水平、提升解題技能的教學(xué)方法. 現(xiàn)借助幾何教學(xué)中，開展習(xí)題變式教學(xué)的實(shí)例說明這樣的教學(xué)方法是如何實(shí)施的.

[關(guān)鍵詞] 習(xí)題變式;變式教學(xué);幾何

習(xí)題變式教學(xué)，是指在設(shè)計(jì)了一道習(xí)題，引導(dǎo)學(xué)生完成習(xí)題以后，在不改變?cè)}本質(zhì)的基礎(chǔ)上，對(duì)問題進(jìn)行延伸，比如更改一個(gè)已知條件、更改未知答案、或者把問題抽象化等，在原題的基礎(chǔ)上延伸出數(shù)道習(xí)題，讓學(xué)生通過回答一系列的習(xí)題來深入理解數(shù)學(xué)問題、培養(yǎng)思維水平、提升解題技能的教學(xué)活動(dòng).

應(yīng)用基本的問題，幫助學(xué)生打好數(shù)學(xué)基礎(chǔ)

教師開展變式教學(xué)，設(shè)計(jì)第一個(gè)問題的要點(diǎn)，是要為學(xué)生優(yōu)選數(shù)學(xué)問題，幫助學(xué)生打好數(shù)學(xué)基礎(chǔ). 打好數(shù)學(xué)基礎(chǔ)的內(nèi)容包括幫助學(xué)生回顧一個(gè)知識(shí)概念、讓學(xué)生了解正確的解題流程、能夠分析出某一類問題解題的重點(diǎn)和難點(diǎn). 教師可以應(yīng)用以下的教學(xué)方法達(dá)到這樣的教學(xué)效果.

第一步，教師必須為學(xué)生優(yōu)選數(shù)學(xué)案例，這一數(shù)學(xué)案例中的知識(shí)點(diǎn)必須有典型性、延伸性、基礎(chǔ)性.

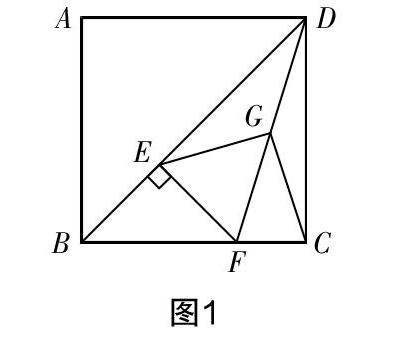
變式1：已知正方形ABCD中，E為對(duì)角線BD上一點(diǎn)，過E點(diǎn)作EF⊥BD交BC于F，連接DF，G為DF中點(diǎn)，連接EG，CG. （1）求證：EG=CG.

該題具有三個(gè)特點(diǎn)：考核的概念具有典型性的特點(diǎn)，只要學(xué)生熟悉直角三角形、三角形的中線、角平分線、邊、高這些概念，就能夠應(yīng)用數(shù)學(xué)知識(shí)解題;考核的內(nèi)容具有延伸性的特點(diǎn)，該題中涉及的幾何圖形包括正方形、直角三角形等一系列幾何圖形，圖形和圖形之間聯(lián)系十分緊密，教師在開展教學(xué)的時(shí)候，只要更改一個(gè)條件，整個(gè)幾何圖形的已知條件都會(huì)發(fā)生變化，設(shè)計(jì)這樣的問題，能夠讓后續(xù)的幾何變式教學(xué)順利開展;題目的起點(diǎn)具有基礎(chǔ)性的特點(diǎn)，該題的第一個(gè)數(shù)學(xué)問題并不復(fù)雜，即使是學(xué)困生，通過閱讀課本，也能找到相應(yīng)的數(shù)學(xué)概念來解題，這是一個(gè)能夠面向所有學(xué)生，鼓勵(lì)所有學(xué)生探索的數(shù)學(xué)習(xí)題.

第二步，引導(dǎo)學(xué)生掌握正確的解題流程.

一名學(xué)生的解題流程如下：繪制出圖形如圖1，證明：在Rt△FCD中，因?yàn)镚為DF的中點(diǎn)，所以CG=FD. 同理，在Rt△DEF中，EG=FD，所以CG=EG.

學(xué)生在解題時(shí)，教師要引導(dǎo)學(xué)生檢查他的證明流程是否存在邏輯漏洞. 如果學(xué)生在證明時(shí)出現(xiàn)了邏輯錯(cuò)誤，便要反思如何應(yīng)用正確的邏輯來分析問題. 教師這樣開展教學(xué)的目的有兩個(gè)：培養(yǎng)學(xué)生的解題技能及幫助學(xué)生夯實(shí)數(shù)學(xué)基礎(chǔ). 變式教學(xué)的后續(xù)問題會(huì)較為復(fù)雜，如果學(xué)生在基礎(chǔ)問題的學(xué)習(xí)中就出現(xiàn)了解題技能不足的問題，那么在解決后續(xù)的問題中會(huì)出現(xiàn)更多的解題漏洞，教師做好這一環(huán)節(jié)的教學(xué)引導(dǎo)，能為后續(xù)的教學(xué)打好基礎(chǔ).

第三步，引導(dǎo)學(xué)生發(fā)現(xiàn)數(shù)學(xué)問題中的重點(diǎn)和難點(diǎn).

教師要引導(dǎo)學(xué)生看到，基礎(chǔ)習(xí)題的解題難點(diǎn)是什么. 教師幫助學(xué)生回顧知識(shí)點(diǎn)的目的是為了幫助學(xué)生積累基礎(chǔ)變式中需要掌握的知識(shí)，后續(xù)延伸的變式都將要應(yīng)用到這些基礎(chǔ)知識(shí).

在這一次的幾何變式教學(xué)中，教師要引導(dǎo)學(xué)生以完成基礎(chǔ)變式的學(xué)習(xí)來驗(yàn)證其是否熟悉了與直角三角形有關(guān)的概念知識(shí)，是否了解相關(guān)的數(shù)學(xué)性質(zhì)等. 教師可引導(dǎo)學(xué)生應(yīng)用思維圖形、概念圖、表格等，讓學(xué)生梳理出相關(guān)的知識(shí)，形成完善的知識(shí)體系. 有一名學(xué)生應(yīng)用表格的方式整理出了直角三角形的性質(zhì)，如表1，當(dāng)學(xué)生應(yīng)用表格整理出直角三角性的性質(zhì)，并熟悉了相關(guān)內(nèi)容以后，便能迅速地突破學(xué)習(xí)重點(diǎn)和難點(diǎn)，理解第一個(gè)變式習(xí)題的解題機(jī)理.

[性質(zhì) 性質(zhì)呈現(xiàn)內(nèi)容 直角三角形的兩個(gè)銳角互余 如果∠C為直角，那么∠A+∠B=90° 直角三角形斜邊中線性質(zhì) 直角三角形斜邊的中線長(zhǎng)度為斜邊的一半 直角三角形三邊的關(guān)系性質(zhì) 勾股定理：a2+b2=c2 直角三角形的邊與角關(guān)系性質(zhì) ∠30°對(duì)應(yīng)的直角邊等于斜邊的一半 ][表1]

應(yīng)用問題的變化，幫助學(xué)生培養(yǎng)思維水平

教師開展變式教學(xué)，設(shè)計(jì)第二個(gè)問題的要點(diǎn)，在于全面地培養(yǎng)學(xué)生的思維水平. 教師要引導(dǎo)學(xué)生看到學(xué)習(xí)知識(shí)、解答習(xí)題的目的不僅是為了完成一個(gè)習(xí)題、獲得一個(gè)答案. 學(xué)生在解答習(xí)題的時(shí)候，要學(xué)會(huì)充分挖掘問題，然后在解決問題的過程中，培養(yǎng)自己的思維水平. 教師可以應(yīng)用以下的教學(xué)方法達(dá)到這樣的教學(xué)目的.

第一步，教師要引導(dǎo)學(xué)生了解他們是學(xué)習(xí)的主體，不能被動(dòng)地做習(xí)題，成為學(xué)習(xí)數(shù)學(xué)知識(shí)的機(jī)器. 學(xué)生必須要思考一個(gè)習(xí)題可以產(chǎn)生怎樣的變化，產(chǎn)生探究知識(shí)的心理.

變式2：（2）將圖1中△BEF繞B點(diǎn)逆時(shí)針旋轉(zhuǎn)45°，參看圖1，取DF中點(diǎn)G，連接EG，CG. 求證：EG=CG.

在傳統(tǒng)的數(shù)學(xué)習(xí)題教學(xué)中，學(xué)生需要解決的是一個(gè)封閉化的數(shù)學(xué)問題，只需要根據(jù)已知條件來分析未知答案，找到問題的答案，便完成了學(xué)習(xí)任務(wù). 在習(xí)題變式教學(xué)中，教師可以通過給出變式2，讓學(xué)生意識(shí)到，雖然教師給出的變式1這個(gè)數(shù)學(xué)習(xí)題是封閉式的問題，但是學(xué)生可以根據(jù)自己的解題需求來讓習(xí)題產(chǎn)生變化，把封閉式的問題變成開放式的問題. 教師應(yīng)用這樣的方法，可以激發(fā)學(xué)生主體性，使學(xué)生意識(shí)到在學(xué)習(xí)時(shí)要應(yīng)用發(fā)散思維來聯(lián)想問題. 教師讓學(xué)生應(yīng)用發(fā)散思維來思考問題，可為繼續(xù)開展變式教學(xué)打好思維基礎(chǔ).

第二步，教師要引導(dǎo)學(xué)生了解數(shù)學(xué)問題可以怎樣變化.

教師要通過變式訓(xùn)練，讓學(xué)生了解數(shù)學(xué)問題可以產(chǎn)生怎樣的變化. 比如在這一次的幾何變式教學(xué)中，教師可以引導(dǎo)學(xué)生看到幾何是研究空間結(jié)構(gòu)及性質(zhì)的一門學(xué)科. 學(xué)生在探究幾何問題時(shí)，要應(yīng)用平移、旋轉(zhuǎn)、拉伸等方式來讓幾何圖形產(chǎn)生變化，學(xué)生需要思考當(dāng)幾何圖形產(chǎn)生變化后，它的已知條件會(huì)發(fā)生什么變化，當(dāng)已知條件變化以后，未知的答案是不是會(huì)產(chǎn)生變化.

第三步，教師要引導(dǎo)學(xué)生拓展知識(shí)，讓學(xué)生把知識(shí)點(diǎn)與知識(shí)點(diǎn)聯(lián)系起來，解決更復(fù)雜的數(shù)學(xué)問題.

比如變式2中，幾何圖形發(fā)生變化以后，教師要引導(dǎo)學(xué)生發(fā)現(xiàn)僅依據(jù)原先掌握的直角三角形性質(zhì)的知識(shí)，是不能解決變式2中的數(shù)學(xué)問題的，那么要解決變式2中的數(shù)學(xué)問題，需要應(yīng)用到什么數(shù)學(xué)概念及數(shù)學(xué)性質(zhì)？有一名學(xué)生應(yīng)用了相似三角形及矩形的知識(shí)，學(xué)生的解題過程如下：連接AG，過G點(diǎn)作MN⊥AD于M，與EF的延長(zhǎng)線交于N點(diǎn)，在△DAG與△DCG中，因?yàn)锳D=CD，∠ADG=∠CDG，DG=DG，所以△DAG≌△DCG，所以AG=CG. 在△DMG與△FNG中，因?yàn)椤螪GM=∠FGN，DG=FG，∠MDG=∠NFG，所以△DMG≌△FNG，所以MG=NG. 在矩形AENM中，AM=EN，在Rt△AMG與Rt△ENG中，因?yàn)锳M=EN，MG=NG，所以△AMG≌△ENG，所以AG=EG，所以EG=CG. 當(dāng)學(xué)生應(yīng)用這樣的方法解決問題以后，教師引導(dǎo)學(xué)生依照梳理變式1中知識(shí)體系的方法來梳理變式2中涉及的知識(shí)，幫助學(xué)生形成更為完善的知識(shí)體系.

應(yīng)用問題的延伸，幫助學(xué)生養(yǎng)成探究習(xí)慣

教師開展變式教學(xué)，設(shè)計(jì)第三個(gè)問題的要點(diǎn)，是要引導(dǎo)學(xué)生學(xué)會(huì)自己延伸問題，養(yǎng)成探究的習(xí)慣. 教師要讓學(xué)生意識(shí)到自己是學(xué)習(xí)的主體，必須學(xué)會(huì)自己延伸問題，找到需要研究的目標(biāo). 學(xué)生只有學(xué)會(huì)結(jié)合自己的學(xué)習(xí)興趣、層次、需求，自己延伸問題，盡可能讓習(xí)題產(chǎn)生變化，才能在解題的過程中學(xué)習(xí)到更多知識(shí).

變式3：（3）將圖1中△BEF繞B點(diǎn)旋轉(zhuǎn)任意角度，參看圖3，再連接相應(yīng)的線段，求證：EG=CG.

變式3是教師引導(dǎo)學(xué)生自己思考以后設(shè)計(jì)出來的問題. 教師要引導(dǎo)學(xué)生把握住設(shè)計(jì)問題的幾個(gè)原則：學(xué)生是否充分發(fā)揮了自己的想象力，并且聯(lián)系更多知識(shí)點(diǎn)，設(shè)計(jì)出更多的問題. 比如在這一次的學(xué)習(xí)中，學(xué)生不僅設(shè)計(jì)出了變式3這樣的問題，還考慮過將變式1中的正方形改成長(zhǎng)方形、菱形、平行四邊形等. 教師要讓學(xué)生養(yǎng)成開放的學(xué)習(xí)心態(tài)，盡可能在探索問題的過程中吸收更多的知識(shí)，比如學(xué)生在延伸問題的過程中希望了解，如果變換了條件，那么原本題目中預(yù)設(shè)的數(shù)學(xué)關(guān)系是否還存在，如果依然存在，證明的依據(jù)是什么，可以應(yīng)用什么數(shù)學(xué)思想來完成證明等. 教師要引導(dǎo)學(xué)生在學(xué)習(xí)變式問題時(shí)，逐步拓展知識(shí)，完善知識(shí)體系.

初中數(shù)學(xué)教學(xué)中可以在幾何教學(xué)板塊開展習(xí)題變式教學(xué)，只要教師把握住變式教學(xué)開展的要點(diǎn)，就能夠幫助學(xué)生積累知識(shí)、培養(yǎng)學(xué)生的思維能力、鍛煉學(xué)生解決問題的能力.