面對稱飛行器橫側向穩定控制設計研究

李天任，張 旋，黃 佩，周 華，郝 穎

（中國運載火箭技術研究院研究發展部，北京，100076）

0 引 言

Nonweiler[1]發現的楔形氣動構型是最早高升阻比面對稱氣動構型，隨后陸續發展出錐形流[2]、吻切錐[3]等面對稱高升阻比構型。在設計飛行條件下，該類構型前緣處產生的附體激波，阻止下表面的高壓氣體橫向“泄露”到上表面，可有效減少飛行器的升力損失[4]，提高其升阻比，進而使其成為高升阻比再入飛行器重要構型之一[4]。面對稱高升阻比再入飛行器，氣動特性復雜，通道間耦合效應強烈，可能導致控制機構的執行效果與設計預期效果相去甚遠。

面對稱再入飛行器的氣動構型在實際應用中，需設計合適的姿態穩定策略及控制參數，使其能沿著既定的目標飛行。本文采用全狀態量反饋控制器，推導出適用于不同狀態的控制穩定條件，設計了相應控制策略，并通過不同工況下的參數調整與運動仿真，驗證了穩定條件適應性與控制策略有效性。

1 橫側向姿態動力學模型

基于中國航天領域常用的機體坐標系[5]，建立非線性運動學與動力學方程：

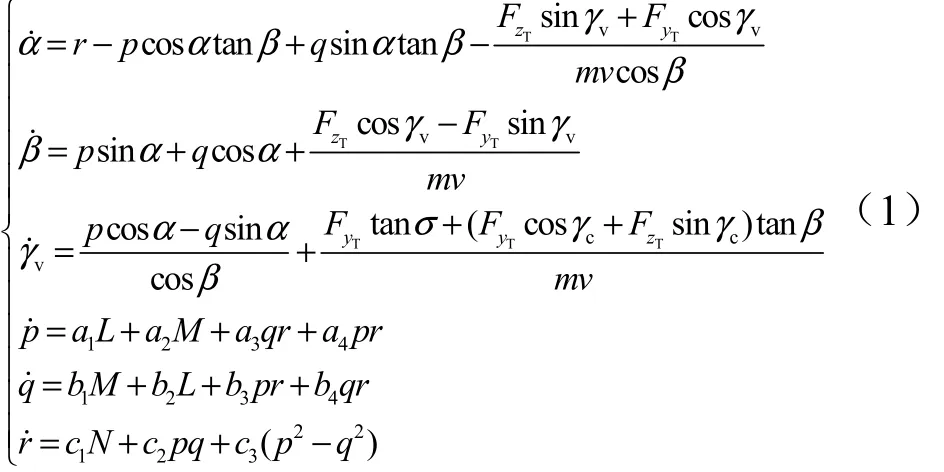
面對稱再入飛行器采用傾斜轉彎（Bank-to-Turn，BTT）控制方式，側滑角始終限定在0°附近，忽略縱向運動及氣動阻尼項對橫側向運動的影響，并將重力因素劃歸制導系統補償，設：δr,δa為飛行器方向舵及副翼舵偏角； Ix,Iy,Ixy為飛行器對體軸 OX，OY的主轉動慣量及慣量積； Q , S, lk為飛行動壓、飛行器參考面積和參考長度；為滾轉力矩系數與偏航力矩系數對側滑角、方向舵及副翼舵偏角的導數。得到基于平衡狀態的橫側向小擾動線性化狀態方程為

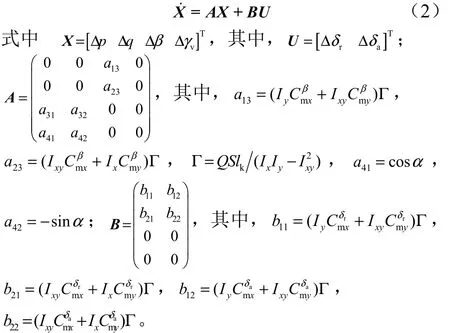
2 控制穩定性分析

2.1 方向舵控制穩定條件

基于式（2），采用全狀態量反饋，得到控制器方程為

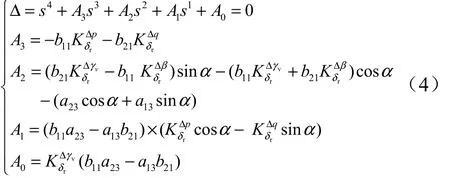
根據勞斯穩定判據，系統穩定的充要條件為

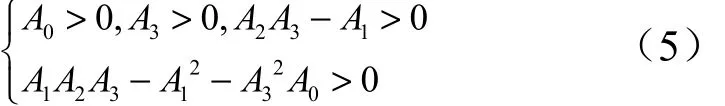
以上充要條件形式復雜，不便于分析，這里推導其必要條件：

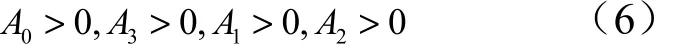
另設：

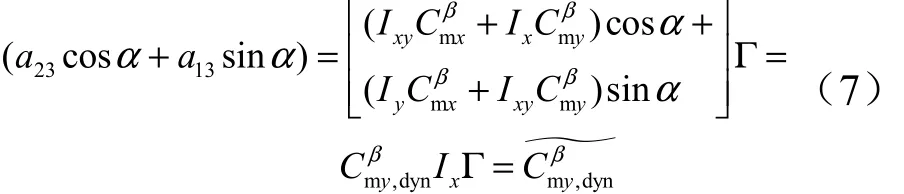
考慮到面對稱飛行器通常要求荷蘭滾模態穩定，本文坐標系下即有，同時限定飛行攻角在，可得以下穩定條件：

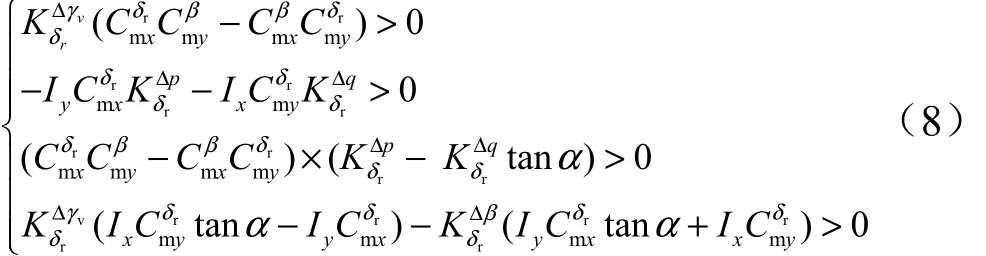
2.2 副翼控制穩定條件

與第2.1節的分析類似，副翼采用全狀態量反饋，得到控制器方程如下：

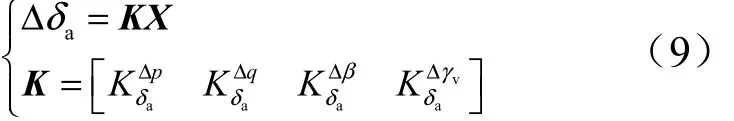
另設：

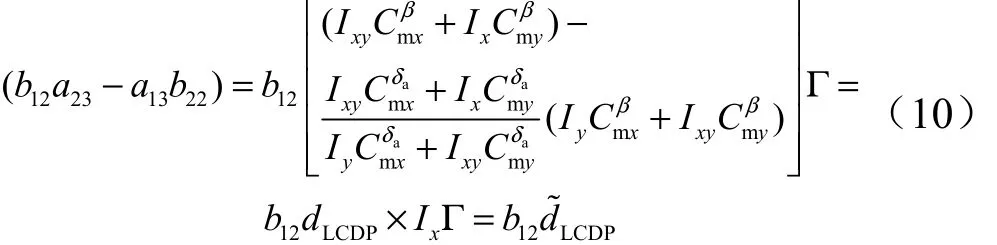
式中 dLCDP為橫向操縱偏離參數（Lateral Control Departure Parameter，LCDP）與 d~LCDP同號。可得以下穩定條件：

2.3 常規控制穩定條件

根據文獻[6]，副翼與方向舵分別控制橫向與側向通道，得到常規控制方程為

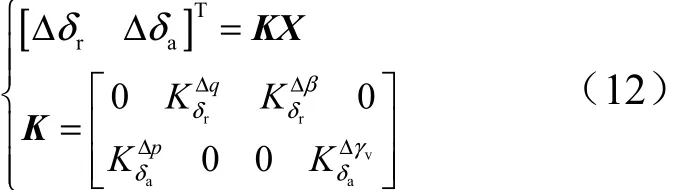
綜合式（8）與式（11），得到如下穩定性條件：

式（13）表明，若飛行器使用常規控制方案實現姿態穩定，則其氣動特性需滿足：

3 控制器設計與仿真

1958年，Moul和Paulson[7]提出的LCDP判據，是高升阻比再入飛行器氣動布局設計與評估的重要指標。因此，本文針對某面對稱再入飛行器，分別選取LCDP為負值與正值兩個典型飛行工況，進行控制器設計與仿真。

3.1 LCDP小于0

此時，飛行器橫側向狀態方程參數取值為：α=10°，a13=-9.57，a23=-0.2885，b11=0.4382，b21=0.1087，b12=-3.294，b22=-0.0642。

這一工況下，按照舵面使用方式不同，設計3類控制策略：

a）策略一：方向舵主導控制橫側向通道，反饋側滑角、傾側角及偏航角速度；副翼增穩，反饋滾轉角速度。

b）策略二：副翼主導控制橫側向通道，反饋側滑角、傾側角及滾轉角速度；方向舵增穩，反饋偏航角速度。

c）策略三：方向舵控制側向通道，反饋側滑角及偏航角速度；副翼控制橫向通道，反饋傾側角及滾轉角速度。

圖1展示了輸入為1°傾側角指令時，系統的狀態響應及舵偏角曲線。

圖1 狀態響應及舵偏角曲線( dLCDP＜0)Fig.1 The State Response, Rudder and Aileron Curve (dLCDP＜0)

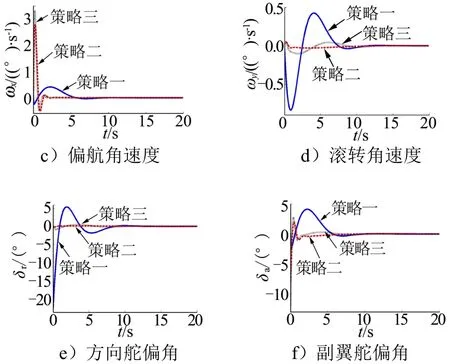
續圖1

由仿真結果可知：

a）副翼主導控制（策略二）與常規控制（策略三）對比：二者在橫向通道的表現較為類似，傾側角、滾轉角速度及副翼舵偏角曲線十分靠近，后者的傾側角跟蹤略顯快速；在側向通道上，后者引入側滑角到方向舵的反饋，因而收斂速度更快。

b）方向舵主導控制（策略一）的機理是先產生負的側滑角，利用飛行器自身橫向靜穩定性較大（ Cmβx＜0，a13=-9.57）的特性，進而產生正的滾轉力矩，實現傾側角跟蹤階躍指令。與策略二、三相比：策略一需要較大的側滑角，另外 Iy與 Ix的比值較大，因此其橫側向通道的收斂速度均慢了不少；階躍響應初期，傾側角偏差反饋使得方向舵負偏角較大，而側滑角尚未大幅增加，正的力矩系數導數（b11=0.4382，0）產生負的滾轉力矩，導致傾側角出現一小段負值。

3.2 LCDP大于0

此時，飛行器橫側向狀態方程參數取值為：α=9°，a13=-17.911，a23=-0.185，b11=0.3705，b21=0.09，b12=-8.361，b22=-0.2322。

根據式（8）、（11）及（13）所列的控制穩定性要求，對前文控制策略進行適當修改，得到LCDPd ＞0時的3類控制策略：

a）策略一：方向舵主導控制橫側向通道，反饋側滑角、傾側角及滾轉角速度；副翼增穩，反饋偏航角速度及滾轉角速度。

b）策略二：副翼主導控制橫側向通道，反饋側滑角、傾側角及偏航角速度；方向舵增穩，反饋偏航角速度。

c）策略三：方向舵控制側向通道，反饋側滑角及偏航角速度；副翼控制橫向通道，反饋傾側角及滾轉角速度；采用副翼方向舵交聯[8,9]（Aileron Rudder Interconnect，AIR）技術，引入控制器參數KAIR，利用方向舵克服副翼的不利偏航力矩。

圖 2為副翼方向舵交聯控制結構框圖，圖 3為dLCDP＞0時的狀態響應及舵偏曲線。

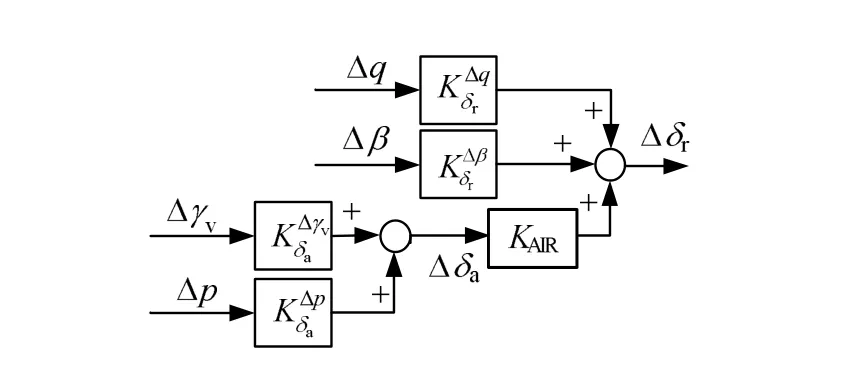
圖2 副翼方向舵交聯控制結構Fig.2 Structure of Aileron Rudder Interconnect Control

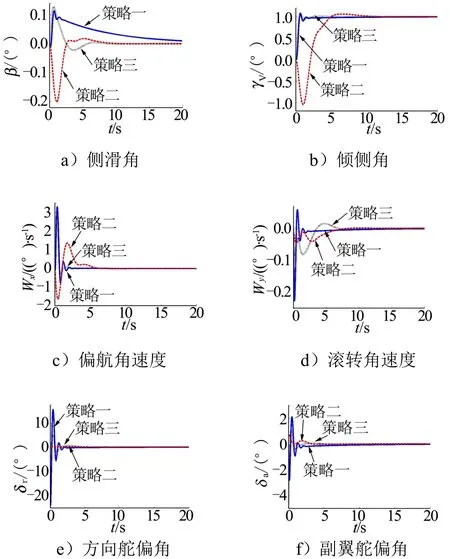
圖3 狀態響應及舵偏曲線( dLCDP＞0)Fig.3 The State Response, Rudder and Aileron Curve (dLCDP＞0)

由圖3所示的仿真結果可知：

a）方向舵主導控制（策略一）與常規+AIR控制（策略三）對比：二者在橫向通道的表現較為類似，傾側角與滾轉角速度曲線十分靠近，副翼舵偏角僅在仿真初始時刻（0.1 s以內）偏差較大，隨后變化趨勢一致；在側向通道上，前者的方向舵需完成橫側向兩通道姿態穩定，因而其舵偏角更大，但側滑角收斂速度仍慢于后者。

b）對于策略一：雖然其側滑角始終為正值，且方向舵偏角為負值，橫向靜穩定性（=-17.911）與力矩系數對方向舵偏角導數（=0.3705）產生的是負滾轉力矩，但由于偏航角速度到副翼的反饋（根軌跡如圖 4所示）提升了系統穩定性，副翼舵偏角為負值，且力矩系數對副翼舵偏角導數為較大的負值（），使得綜合的滾轉力矩為正，傾側角正向增大。策略三的情形與之類似。

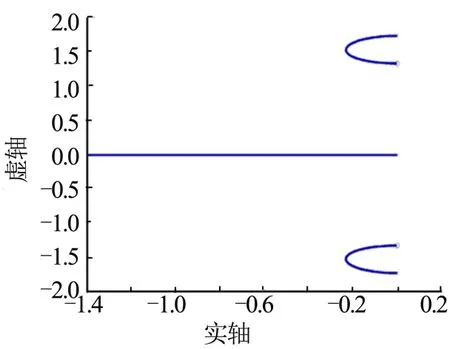
圖4 副翼反饋偏航角速度根軌跡Fig.4 Root Locus Diagram for the Feedback from Yaw Angular Velocity to the Aileron

4 結束語

本文以面對稱再入飛行器為研究對象，首先從橫側向狀態方程出發，基于全狀態量反饋，推導了方向舵控制、副翼控制及常規控制的穩定條件。隨后，針對LCDPd ＜0與LCDPd ＞0兩種工況，各自設計了方向舵主導、副翼主導及常規（+AIR）3類橫側向控制策略。最后，仿真算例顯示3類策略均可實現姿態穩定控制，驗證了穩定控制條件對不同特性飛行器的有效性與適應性。文中的研究，亦可適用于升力體、融合體、翼身組合體等其它高升阻比面對稱構型飛行器，對工程實際應用具有一定參考價值。