解決立體幾何問題中空間向量的運用
云南省曲靖市民族中學 李光所
一、立體幾何問題中運用空間向量的價值
1.簡化立體幾何解題步驟
在立體幾何問題解決中,運用空間向量思維方法可將空間問題轉化為平面問題、幾何問題轉化為代數問題進行解決,簡化立體幾何的傳統解題過程。空間向量主要解決的是點、線、夾角和距離之間的問題,這種解題方式可減少學生對數學思維的轉換難度,同時將原題中的輔助線替代為坐標系,還能夠促使解題步驟與過程的進一步簡化,體現出空間向量解題的優越性。
在立體幾何解題中,傳統的解題方法是學生先利用相關的定理和公式明確解題思路,之后再運用多種思維進行轉換,這樣才能完成解題過程。傳統解題方法過于復雜,對于思維轉換能力偏差的學生而言,增加了解題的困難程度。而運用空間向量解決立體幾何問題,雖然在一定程度上增加了計算過程的復雜性,但是卻能夠幫助學生快速理清解題思路,淡化由“形”到“形”的推理過程,進一步明確解題目的,提高學生解題能力。
3.賦予數學解題的簡捷美
在立體幾何解題中,可利用空間向量的直角坐標運算解決空間垂直與平行的問題,利用向量的夾角公式求出兩條直線的夾角和線面夾角,利用向量的距離公式求出兩點間的距離和兩面角的平面角。通過運用空間向量方法解決較為復雜的立體幾何問題,能夠使解題過程清晰明了,解題書寫內容簡捷和諧。
二、在立體幾何問題中空間向量的運用方法
空間向量主要運用于立體幾何中的空間垂直證明、空間平行證明、空間角求解和空間距離求解四個方面,下面對垂直與平行問題和空間角問題的解題方法進行例題探討。
1.空間向量在解決平行垂直問題中的應用
在運用空間向量證明線面平行時,應明確兩種解題思路:一是可根據線面平行的判定定理,通過證明直線的方向向量與平面內一條直線的方向向量平行得出結論;二是通過證明直線的方向向量與平面的法向量垂直得出結論。在運用空間向量證明面面垂直時,也可采用兩種解題思路:一是運用判定定理通過證明線線垂直得出結論;二是通過證明兩個平面的法向量垂直得出結論。
例1 如圖1 所示,在底面為矩形的四棱錐P-ABCD 中,ABCD,E 是PC 中點,F 是PD 中點,PA=AB=1,BC=2。求證:(1)EF ∥平面PAB;(2)平面平面PDC。
4.1.1 實施“亮證經營”制度,在超市顯著位置設置食品安全信息公示欄,公示以下信息:食品經營許可證和營業執照;全部食品經營人員的健康檢查證明(原件、復印件或者電子版);門店負責人和食品安全管理員的照片、姓名、培訓證明(原件、復印件或者電子版)。

圖1
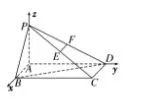
圖2
證明:以A 為原點建立空間直角坐標系(如圖2 所示),可知A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,1),由此可獲得
2.利用空間向量在空間角問題中的應用
在立體幾何中,求空間角與距離是一類較為重要的問題,在歷年的高考中均有此類題型出現,由此使得空間角成為立體幾何教學的重點內容。在解決空間角問題的過程中,可對空間向量進行合理運用,通過空間向量的引入,能夠為代數方法解決立體幾何問題提供有效的工具。在解題時,可以用定量計算代替定性分析,這樣一來,能夠使煩瑣的推理論證過程得以簡化,有助于加快解題速度,提高解題效率。
例2 如圖3 所示。在Rt △ABC 中,∠BCA=90°,現將△ABC 沿著平面ABC 的法向量平移至△A1B1C1的位置處,已知BC=CA=CC1,取A1B1、A1C1的中點D1和F1。求BD1與AF1所成角的余弦值。
解:以點C 作為坐標原點,建立空間直角坐標系C-xyz,具體如圖4 所示。
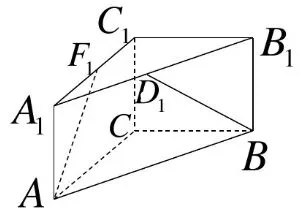
圖3

圖4
設CC1=1,則
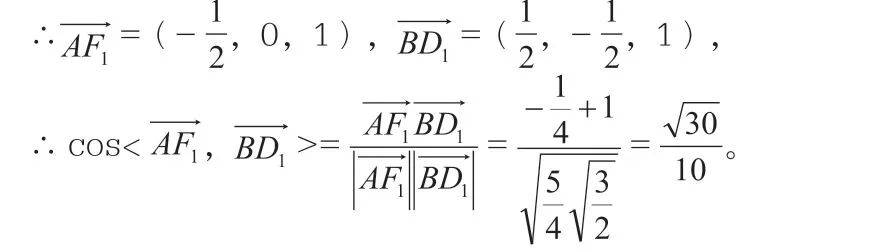
∴BD1與AF1所成角的余弦值為
例3 如圖5 所示,在長方體ABCD- A1B1C1D1中,AB=5,AD=8,AA1=4,M 為BC1上的一點,且B1M=2,點N 在線段A1D 上,A1D ⊥AN。求AD 與平面ANM 所成角的正弦值。

圖5
解:由圖可知,A(0,0,0),A1(0,0,4),D(0,8,0),
通過上述例題的分析可以看出,在空間角求解中,對空間向量進行運用,能夠使煩瑣的解題過程得以簡化,為學生快速求解提供了有效的方法。
總而言之,在高中數學教學中,將空間向量運用到立體幾何問題的解決中來,有利于簡化解題過程,幫助學生形成完整的解題思路,對培養學生發散性思維和提升學生數學學習能力起著積極作用。在數學解題中,教師要引導學生掌握空間向量解決立體幾何平行問題、垂直問題、空間距離問題以及空間角問題的方法,幫助學生提高解題效率和準確性。

