數形結合思想在小學數學教學中的應用
貴州省遵義市播州區團溪鎮團溪小學 羅曉琴
所謂數形結合思想,就是結合合理性的數學關系和空間形式轉換,有效解決數學問題的思想體系,在數學教學中利用這種轉換模式能將數學語言和直觀圖形進行結合,從而提升學生對于抽象數學概念以及數學關系量化結構的理解,夯實學生的學習基礎。
一、以形助教滲透數形結合思想
一方面,在數形結合思想體系內,要想提升學生的綜合素質,就要在“形”學習的基礎上合理滲透“數”的相關思想。學生從學習20 以內數字、100 以內數字一直到學習萬以內數字,不僅要完成會認、會讀的教學目標,還要了解數字的組成。為了夯實教學基礎,教師就要借助“形”引導學生過渡到對“數”本質的認知。
例如,圖一中借助有序的立體圖形變化,學生就能直觀感受到從1 到1000 的變化,這種搭建的方式也能指導學生了解十進制的關系,抽象地講解計數單位無法為學生提供直觀感受,但是利用圖形就能引導學生進一步了解相關內容。

圖1
另一方面,類比思想能有效提升學生對于數形結合的認知水平,確保學生能直觀感受“數”的含義。例如,在講解“小數初步認知”的過程中,書中標注筆記本每本3.15 元、鉛筆每支0.59 元、格尺每把1.06 元、鋼筆每支6.66 元,要求學生按照“××元是××元××角××分”的形式進行填寫,并且指導學生對3.15 進行認讀,讀作三點一五,這樣就能有效滲透小數的內涵,利用類比的方式引導學生進一步認識貨幣。正是借助這種直觀圖形的形式有效提升了學生對相關知識的認知能力,也為全面提高學生學習效率奠定了堅實基礎。需要注意的是,在教材的編排方面,學生只有在“形”的輔助下才能更好地明確小數部分的意義和整數部分意義的區別,確保能提升對相關知識的內化能力,提高學生的綜合素質。
二、以數輔形滲透數形結合思想
在小學數學教學過程中,對于一些容易混淆的知識點,教師要合理建立完整的“以數輔形”的教育機制,確保能提升學生對相應知識體系的認知能力,從而形成舉一反三的教育教學流程,提高學生經驗提取的能力,也為學生全面提高自身水平奠定基礎。
例如,在講解“倍的認識”的過程中,其本身是二年級上學期數學中較為關鍵和具有一定難度的知識點,一方面要了解“一個數是另一個數的幾倍,應用除法”,另一方面要了解“求一個數的幾倍是多少,用乘法”。
首先,求解一個數是另一個數的幾倍,教師可以利用畫圖的方式,表現出12 是4 的3 倍,見圖2,學生就能建立“倍數”的基本模型,并且能了解每份一樣多的含義,能進一步內化對應的知識點。正是借助這種畫圖的過程,學生能建立直觀體驗,且能了解倍數和除法之間的關系,進一步對類比的數據進行分析,確保能提高學習效果。

圖2
其次,求一個數的幾倍是多少,依舊是應用圖形,引導學生理解4 的3 倍是多少,按照畫圖進行分析對照,就能確保學生能理解乘法的具體含義,見圖3:
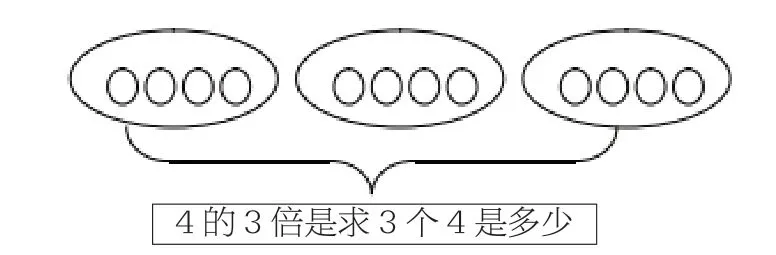
圖3
最后,只有建立完整的數形結合教育教學體系,才能指導學生進一步理解數量關系的結構,并且提升學生將數量關系和空間關系進行互聯的能力,維護學生的學習效率和基本數學素養。最關鍵的是,數形結合有效將抽象關系外顯化,引導學生提升解決問題和理解問題的能力,也為全面分析以及選擇對應數學策略創設了良好的環境,為學生進一步提高數學素養奠定了堅實的教學基礎。
三、數形結合綜合應用
在數形結合教學體系內,教師要對表層知識掌握機制進行明確處理,將數形結合的思想作為基礎體系,從而引導學生在對表層知識學習的過程中掌握具體的方法和手段,一定程度上提高學生的基礎知識水平和基本技能,也為后續提升教育教學效果提供保障。
例如,在講解數學概念的過程中,教師也可以將整數、小數、分數作為三個基本主題,要求學生利用圖形歸納的方式對三個不同體系的數字結構進行描述,引導學生構建思維導圖,將相應知識點進行匯總,從而提高學生利用數形結合思想解答問題的綜合能力,確保能提升學生的認知思想水平。
也就是說,在數形結合思想綜合應用的過程中,教師要引導學生建立相互轉化的思想認知,提升對知識的理解程度和問題解決能力,確保學生能充分掌握數形結合的應用要點,并且將這種數學思想實際應用在做題中,為后續知識點的講解創設良好的教學平臺。
總而言之,數形結合是小學數學教育教學工作中重要的數學思想體系,需要引起教師的高度關注,教師要在課堂教學和練習鞏固中有效培養學生形成相應的思想認知,從而提高學生應用能力,確保學生能在解題過程中充分發揮數形結合思想的優勢,提高答題效率和準確率。

