考慮管壁導熱的方管內熔鹽混合對流傳熱數值模擬

楊岑玉，孟 強，王 樂，陳夢東，胡 曉，徐桂芝

（全球能源互聯網研究院有限公司，先進輸電技術國家重點實驗室，北京 102209）

能源是人類生存和發展的物質基礎，是經濟和社會發展的重要資源。進入21世紀以來，能源需求逐年旺盛，能源供應形勢趨于緊張，能源資源正度越發激烈[1]。化石燃料仍是全球能源消費的主要構成，并導致越來越嚴重的問題。尋找替代能源既可以解決、緩解化石能源短缺，又可以避免因化石能源燃燒導致的生態環境惡化。

可再生能源在滿足能源需求、改善能源結構、減少環境污染等方面起到了巨大作用。太陽能在全球絕大部分地區普遍存在，并且利用方式多樣，為常規能源缺乏的國家和地區提供解決能源問題的理想選擇。太陽能熱發電是太陽能利用的重要形式之一，可與大規模低成本蓄熱系統相結合，并且系統中的熱功轉換部分可采用常規火力發電機組，技術成熟、發電平穩、可控輸出，符合發電方式的基本要求，是理想的發電技術。太陽能熱發電技術可產生大量電能，是最有可能代替傳統能源方式的可再生能源利用方式之一[2]。

典型的太陽能熱發電系統主要由聚光集熱子系統、蓄熱子系統、熱動力發電子系統等主要部分能夠成[3]。太陽能在利用過程中具有間歇性，太陽輻射受到晝夜條件以及天氣變化等的影響，為了保證整個系統在滿足功率要求的情況下平穩運行，系統必須依靠儲存的太陽能來維持正常運行。因此，蓄熱子系統是太陽能熱發電系統中必不可少的重要組成部分。

熔融鹽因為具有適用溫度范圍廣、使用壓力低、導熱性能好、比熱容大、黏度較低、熱穩定性高、安全易得、價格低廉等優點受到廣泛關注[4-6]，目前熔融鹽作為傳蓄熱工質已經在太陽能熱發電領域得到了應用[7]，并取得了顯著效果。美國Solar Two電站將熔融鹽作為新的傳蓄熱介質應用于太陽能熱發電系統中，其使用1440噸混合熔鹽(60%NaNO3+40%KNO3，質量分數)作為傳蓄熱工質，實現了105MW?h的蓄熱能力，折合3小時的汽輪機滿負荷運行[8]。西班牙Gemasolar[9]19MW塔式熔鹽傳熱太陽能熱電站于2011年建成運行，總計使用8500噸混合熔鹽，具備24小時連續發電能力，年運行小時數達到6500小時，年發電量為1.1億度電。同年，西班牙建成了采用二元混合硝酸鹽作為蓄熱工質的Arcosol 50電站，實現了7.5小時的蓄熱能力。2012年西班牙又建成了基于熔鹽蓄熱的50MW商業運行電站Aste 1A、Astexol II，實現了8小時的蓄熱時長[10]。

熔融鹽對流傳熱特性對傳熱設備的設計具有指導意義，并且決定著太陽能熱發電的效率，得到了國內外學者的關注。美國橡樹嶺國家實驗室的HOFFMAN對電加熱情況下的NaOH、Flinak（NaF、LiF、KF混合物）、三元混合硝酸鹽Hitec在圓管內對流換熱情況的進行了研究，并認為該混合熔鹽在換熱設備中用作傳熱流體時，可 用MCADAMS，DITTUS和BOELTER以 及COLBURN提出的標準關聯式進行設計[11]。20世紀80年代，ALLMAN等[12]對熔鹽強化傳熱進行了研究，其研究了熔鹽在異型管蒸氣發生器中的換熱。吳玉庭等[13-14]對圓管內硝酸鹽的強制對流傳熱特性進行了實驗研究，并擬合了實驗關聯式。在此基礎上，特別研究了橫紋管內熔鹽強制對流傳熱特性和流動特性，得到了換熱和阻力的無量綱準則關聯式，評價了橫紋管的綜合強化傳熱效果。

在熔鹽實際利用過程中，存在非均勻加熱，固體表面和流體間存在溫度差異，由密度梯度導致浮升力效應，進而與主流方向流動過程疊加形成混合對流。國內外許多研究者對空氣、水、非牛頓流體、納米流體等多種工質在不同管路通道內的混合對流傳熱過程進行了研究，發現了混合對流過程中流型以及傳熱特性的變化，對混合對流過程中強化傳熱的原因進行了分析，但是目前國內外針對熔鹽混合對流傳熱的研究很少。另外，管壁導熱會對熔鹽混合對流傳熱過程產生一定的影響。本文數值模擬研究了考慮管壁導熱影響的熔鹽混合對流傳熱過程。對水平方管單面加熱時的壁面溫度、傳熱系數以及無量綱參數的變化規律進行了模擬研究，并將結果與流型判定圖和經典關聯式進行對比，進而分析了熔鹽混合對流傳熱特性。

1 模型建立

1.1 模型控制方程

（1）質量守恒

連續性方程：流體在流動過程中滿足質量守恒定律，控制體內單位時間的流體凈流出質量總和等于其因密度變化而減少的質量，方程表述如下

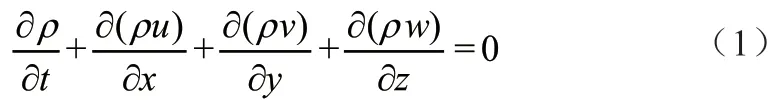
本文視流體流動過程為不可壓縮流動，方程可進一步簡化為

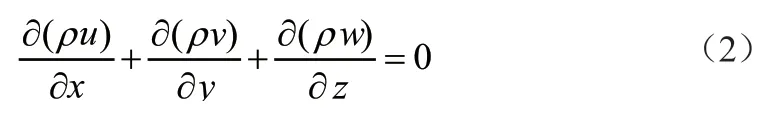
式中，u、v、w分別為x、y、z方向上的速度分量；ρ為密度；t為時間。

（2）動量守恒

根據牛頓第二定律，給定的流體微元的動量/時間變化率等于在其上各種外界作用力之和。針對本課題的模擬過程，流動過程僅受重力作用，表述如下：

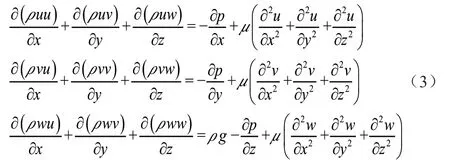
（3）能量守恒

根據熱力學第一定律，微元體中能量的增加率與進入微元體的凈熱流通量及質量力與表面力對微元體所做功之和相等，模擬過程中忽略由黏性耗散導致的加熱源時，可簡化為

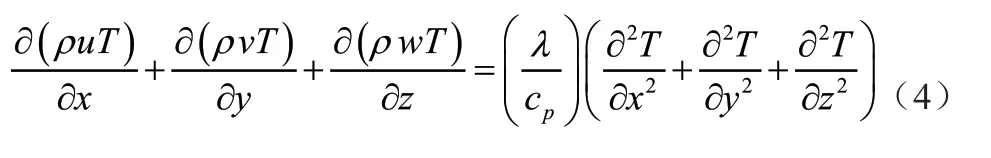
式(4)中，λ是流體導熱系數，cp是定壓比熱容，T是溫度。

固體壁面導熱遵循能量守恒定律和傅里葉定律，可得導熱微分方程為

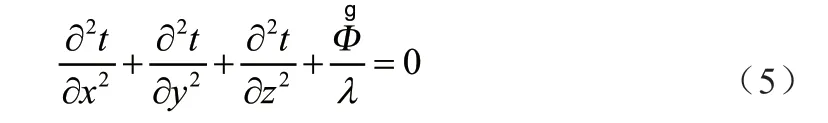
本文采用FLUENT軟件的雙方程RNGκ-ε模型，對熔鹽混合對流進行數值模擬。雙方程κ-ε模型為目前使用最為廣泛的湍流模型，原標準κ-ε模型忽略了漩渦的影響，RNGκ-ε模型就此對其進行了改進，并給出了普朗特數的一個解析式，且對低雷諾數流動黏性情況下提供了解析公式，由此提高了適用范圍和計算精度，非常適用于主要影響因素為浮升力二次流影響的熔鹽混合對流模擬過程。

因此，在實際計算過程中，還需附加湍流輸運方程

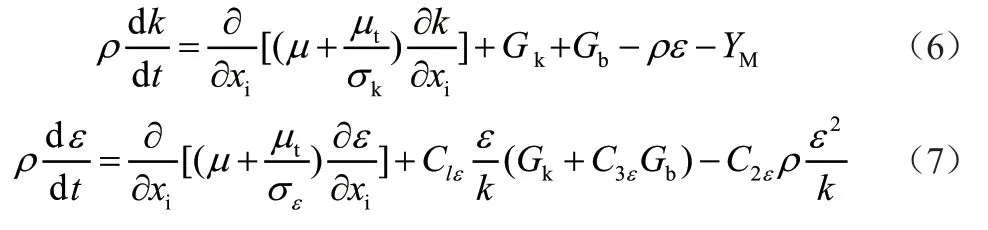
式中，Gk是由平均速度梯度引起的湍動能產生；Gb是由浮升力影響引起的湍動能產生；YM為脈動膨脹對總耗散率的影響；αk、αε分別為湍動能和耗散率的有效普朗特數的倒數；μ為黏度，μt為湍流黏性系數。C1ε、C2ε、C3ε為經驗常數，軟件中默認為常數，σk、σε分別為湍動能k與耗散率ε默認值。

1.2 幾何模型

對熔鹽在水平方管內的流動和傳熱過程進行模擬，考慮壁面導熱影響，重力方向沿y軸向下，方管管寬為19mm，管長為1000mm，壁厚為3mm，方管幾何模型如圖1所示。數值模擬的邊界條件包括：入口邊界流速與溫度；出口邊界設定為常壓；方管壁面沒有滑移，全浮升力效應設置為開啟；壁面為定熱流密度加熱方式；考慮壁面導熱；FLUENT計算模型采用雙方程RNG，κ-ε計算模型；判斷收斂的條件為殘差值10-6～10-8，迭代次數為10000次，求解過程中所有結果均達到收斂。

1.3 混合熔鹽物性參數

混合熔鹽由于具有高熱穩定性，工作溫度寬，價格低等優點，在光熱發電和核能領域中作為傳熱工質應用廣泛。本文流體工質選用Hitec混合硝酸鹽 (NaNO3-NaNO2-KNO3，7%-40%-53%)，其參數包括熔點142℃，沸點680℃。

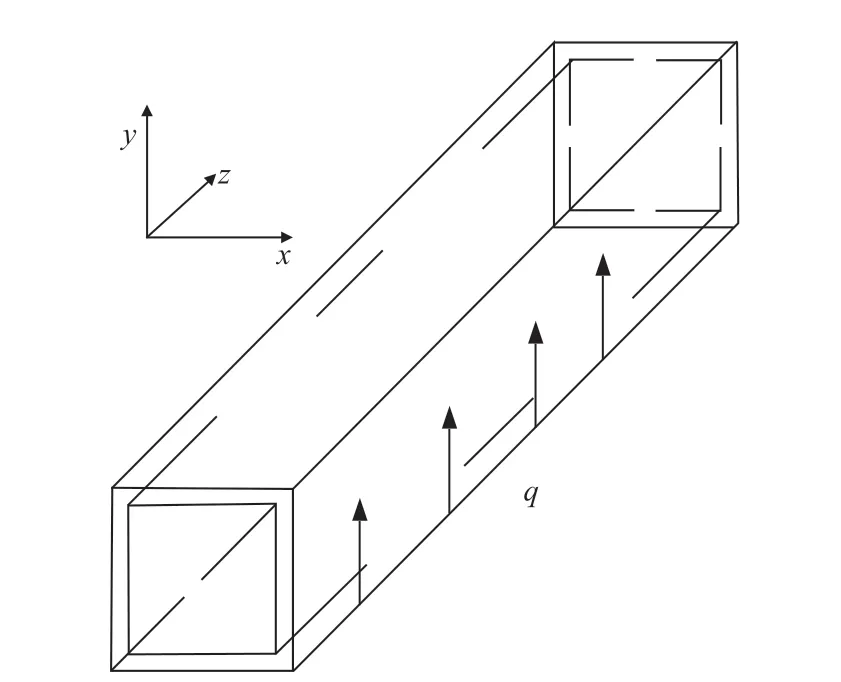
圖1 方管幾何模型Fig.1 Geometry of sqaure tube

由于熔鹽為新型工質，FLUENT材料數據庫中無法提供，因此需要編寫UDF（User-Defined Function）對熔鹽材料進行補充。UDF為FLUENT軟件提供的一個用戶接口，可采用C語言編寫的方式對Fluent模塊數據進行補充。

Hitec熔鹽的主要物性參數為：①密度 （熔化后液態區間內）：ρ=2287.7993-0.7484T；②定壓比熱容 （熔化后液態區間內）cp=1507-0.1T；③導熱系數 （熔化后液態區間內）λ= 0.8099-7.827×10-4T+1.043×10-7T2；④動力黏度：μ= 0.06284-2.253×10-4T+2.7903×10-7T2-1.1738×10-10T3；

固體壁面材料為不銹鋼（steel），物性參數如下： 密度ρ=8030kg/m3；定壓比熱容cp=502.48J/(kg?K)；導熱系數λ=16.27W/(m?K)。

1.4 驗證邊界條件與網格劃分的無關性

研究中采取對模型進行共5種網格劃分的方法來檢驗仿真實驗結果與網格劃分的無關性，如圖2所示。不同網格的仿真結果顯示當網格數量≥25×25×1000時流體溫度的一致性較好，其他較小的網格劃分的偏差較大。因此，本文在綜合考慮計算準確度與消耗時間后，采用了25×25×1000的網格劃分。

2 模擬結果

2.1 模型驗證

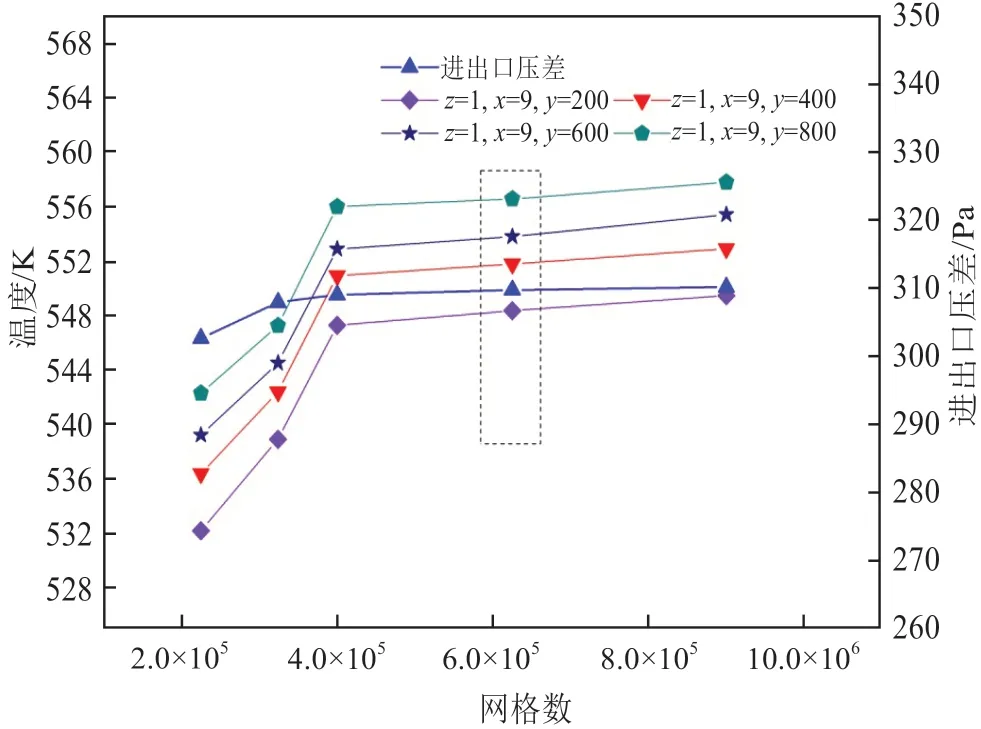
圖2 網格無關性驗證Fig.2 Grid independent validation

研究中對模擬結果的可靠性進行了判定，模擬結果處于湍流混合對流區域內。為進一步驗證結果的準確性，本文將模擬結果與前期獲得的實驗結果進行了對比。實驗流程圖如圖3所示。實驗過程中通過對方管測試段進行底面非均勻加熱，使得熔鹽在流動過程中產生浮升力效應進而形成混合對流過程，通過測量系統對各部分溫度進行記錄，結合熔鹽流量、非均勻加熱熱流密度等已知參數進一步計算熔鹽換熱系數、對應的相關無量綱參數等，并通過對熔鹽泵和加熱器等設備的調節，以達到不同工況的情況，獲得其變化規律，進而得到水平方管內底面加熱情況下熔鹽混合對流傳熱特性。模擬結果與實驗結果對比情況如圖4所示。可以從圖中看出模擬結果與實驗結果符合程度較為良好。考慮壁面導熱模擬結果與實驗結果更為接近，偏差在±10之間。該驗證結果一方面對于熔鹽在非均勻加熱過程的流動方式為混合對流進行了驗證，另一方面對于模擬過程所選用的計算模型的可靠性進行了確認。

2.2 流動特性

圖5為方管單面加熱工況為加熱熱流密度200 kW/m2，軸向流速達到0.3 m/s，主流方向上z=100 mm處的橫截面速度分布。

從圖5的流速分布圖中可以看出外框藍色部分為管壁壁厚區域，三種加熱方式與不考慮壁面導熱的結果[15-16]趨勢相同，均呈現出主流核心區的流速相對較高，且流速分布從中心向四周逐漸降低的趨勢。與不考慮壁面導熱的模擬結果[15-16]流動特性相比，可以看出考慮壁面導熱結果流速分布相對更加均勻。從三種加熱方式流線分布圖中可以看出，底面加熱和側面加熱方式同樣也產生了可觀的渦流，頂面加熱方式流線向核心區匯聚，產生了渦流形成的趨勢。產生渦流的原因是由非均勻加熱所引起的浮升力現象造成，由于考慮壁面導熱，在非均勻加熱過程中，熱量會通過壁面導熱方式從加熱面迅速向非加熱面傳遞，非均勻加熱的效果弱于不考慮壁面導熱的結果，溫度分布以及流線分布上所體現出的結果從程度上來說相對較弱，但是這樣的結果更加符合現實應用中的情況。

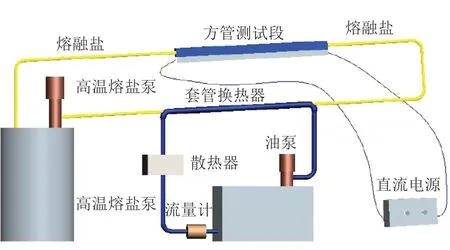
圖3 熔鹽混合對流傳熱實驗原理圖Fig.3 Schematic of molten salt mixed convection experiment

圖4 實驗結果與數值模擬結果對比圖Fig.4 Comparison between the simulated data and experimental data

圖6為方管單面加熱工況為加熱熱流密度200kW/m2，軸向流速達到0.3m/s，主流方向上z=500mm處的橫截面速度分布圖和流線圖。

從圖6可看出流速基本已經發展穩定，并形成了穩定渦流。其中，底面加熱情況下產生了兩個渦流，側面加熱情況下產生了一個渦流，頂面加熱產生了兩個渦流。不考慮壁面導熱的模擬結果顯示，頂面加熱產生了四個渦流：兩個渦流位于上部，靠近頂部加熱面，是由非均勻加熱浮升力現象產生；另外兩個渦流位于截面下部，靠近壁面，是由于頂面加熱過程中失穩現象所造成[15-16]。在考慮壁面導熱的模擬結果中，由于溫度通過導熱方式迅速向壁面傳遞，因此由于頂部非均勻加熱所產生的失穩現象不復存在，由其造成的截面下部的渦流也進而消失，只剩下由混合對流浮升力現象所產生的兩個靠近加熱面的渦流。

圖5 z=100時的速度分布Fig.5 Velocity distributions at z=100

2.3 傳熱特性

圖7為底面加熱方式，加熱熱流密度為200 kW/m2，軸向流速達到0.3 m/s，主流方向各橫截面處的溫度分布情況。

從圖中可看出，由于考慮了壁面導熱，熱量迅速從加熱壁面向各壁面傳遞，使得各壁面溫度迅速上升，進而可以對近壁面處的流體進行加熱，從而產生這種類似尖狀的溫度分布，流體的溫度分布結果相比于不考慮壁面導熱結果更加均勻，整體的結果與不考慮壁面導熱的模擬結果保持相同，溫度隨流動過程的深入呈上升的趨勢。原因同樣在于混合對流過程中所產生的浮升力效應，在兩底角位置處的渦流對流動過程產生了擾動，加強了流體傳熱能力，因此呈現出尖狀分布的特點，另外隨著流動過程的深入，流體溫度在加熱面的持續加熱下穩步上升，壁厚處的溫度也由于導熱的存在逐漸上升，相比于不考慮壁面導熱的結果，考慮壁面導熱的結果溫度分布更加均勻。

圖8為側面加熱方式，加熱熱流密度為200 kW/m2，軸向流速達到0.3 m/s，主流方向各橫截面處的溫度分布情況。如圖7所示，由于存在壁面導熱，熱量傳遞速度更加迅速，溫度分布更加均勻，熱量不再是單一的從加熱壁面像近壁面流體傳遞，而是首先通過導熱傳遞到各壁面，進而傳遞給流體。左側加熱面溫度明顯高于其他壁面，因此近壁處的流體溫度高于其他區域，溫度差的存在使得流體內部產生密度梯度，進而產生浮升力效應，在混合對流過程中對流動過程和傳熱過程產生影響。

圖6 z=500處速度分布Fig.6 Velocity distributions at z=500

圖9為頂面加熱方式，加熱熱流密度為200kW/m2，軸向流速達到0.3m/s，主流方向各橫截面處的溫度分布情況。如圖8所示，壁面導熱的存在使得在頂面加熱過程中，溫度的分布更加均勻，產生了兩個由浮升力現象所產生的靠近頂部加熱面的渦流。由于頂部渦流的存在，兩頂角處流體的溫度相對其他區域溫度更高，這正是由于混合對流過程中所產生的渦流對流體傳熱過程進行強化的體現。

2.4 無量綱參數變化關系

2.4.1Nu數隨Ri數的變化規律

圖10～圖12為3種方式情況下，不同位置處的局部Nux數隨Ri數的變化規律。從3幅圖中曲線的變化情況中可以看出，局部Nux數隨流動過程的深入呈現出先減小后增大的趨勢，當局部Nux數降到最低點后，隨無量綱長度的增加而增長。原因在于入口段熱邊界層厚度迅速增長，導致流體的局部傳熱能力不斷下降至最小值，隨著加熱過程的發展，流體內部產生密度差，在浮升力效應的影響下產生渦流，增強了傳熱效果，因此局部Nux數持續上升。

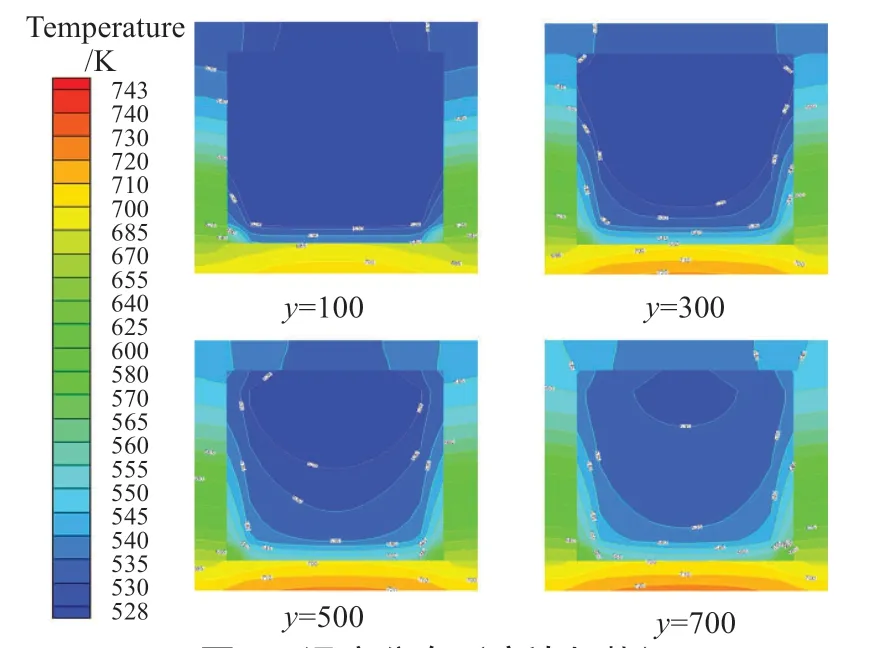
圖7 溫度分布（底邊加熱）Fig.7 Temperature distributions (bottom heated)

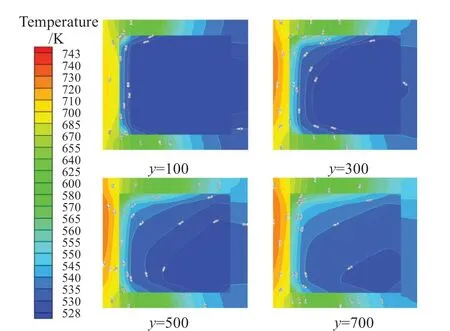
圖8 溫度分布（側邊加熱）Fig.8 Temperature distributions (one side heated)

2.4.2 局部Nux數隨Re數的變化規律

圖13為底面加熱熱流密度為200kW/m2時，不同位置處的局部Nux隨Re數的變化規律。從曲線走勢可以看出，Re數越大，Nux越大，與Nux隨Ri數變化規律相同，且同樣是先減小至最低點后增大。Re數是表征流體流速的無量綱參數，即混合對流過程中入口流速越大，局部傳熱能力越強。側面和頂面加熱情況變化規律與底面加熱情況結果相同。

2.4.3Ri數隨Re數的變化規律

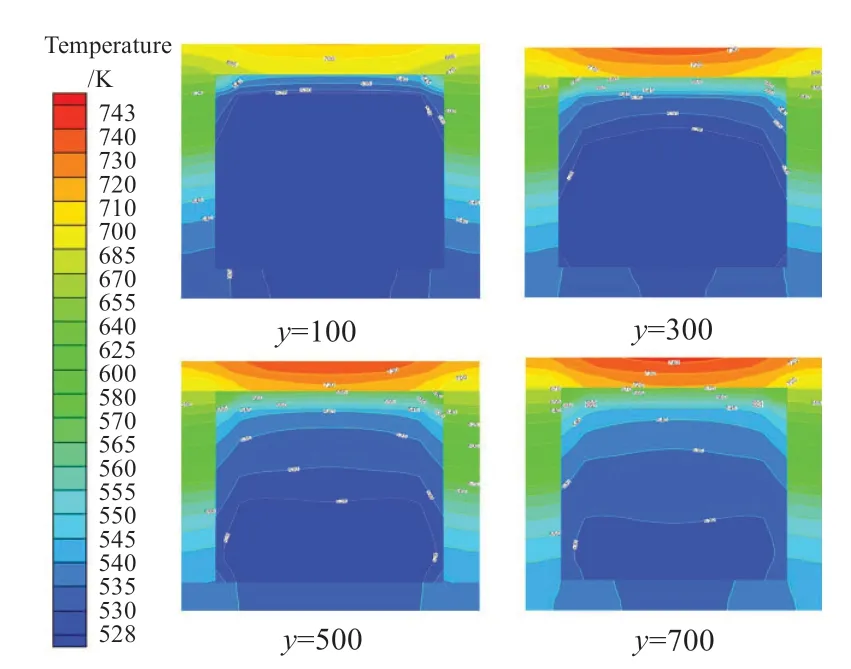
圖9 溫度分布（上方加熱）Fig.9 Temperature distributions (top heated)

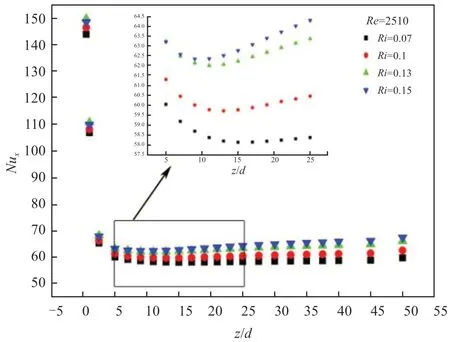
圖10 局部Nux隨Ri數變化規律（底面加熱）Fig.10 The relationship between local Nusselt number and Richardson number (bottom heated)

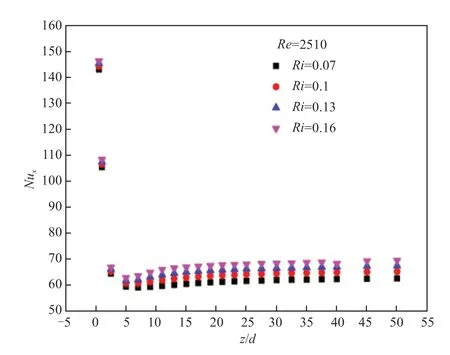
圖11 局部Nux隨Ri數變化規律（側面加熱）Fig.11 The relationship between local Nusselt number and Richardson number (lateral heated)

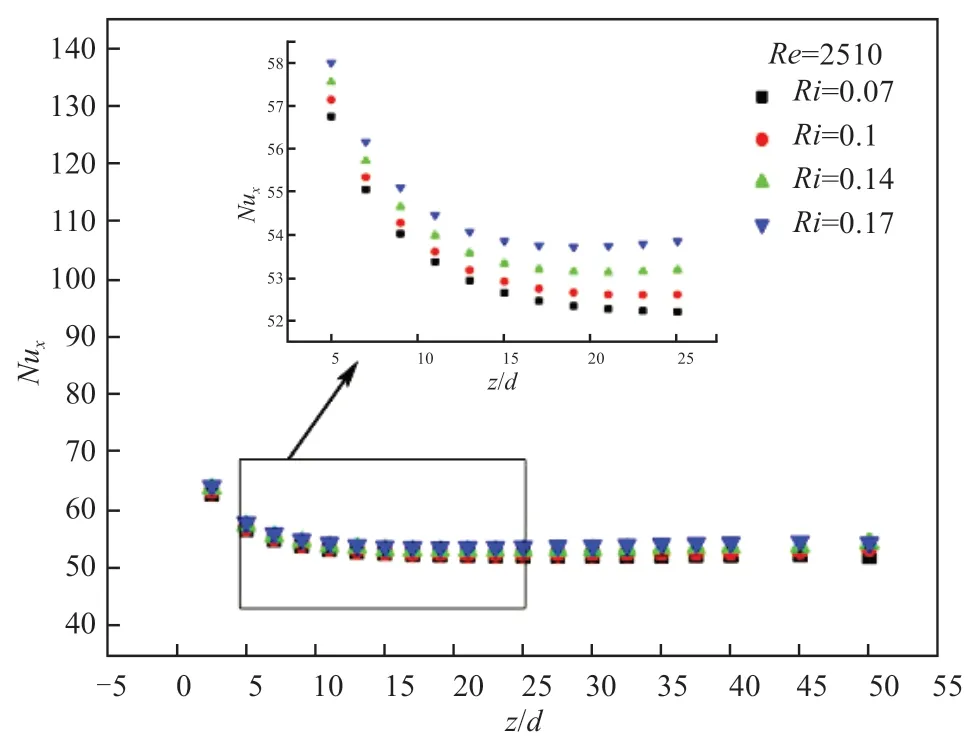
圖12 局部Nux隨Ri數變化規律（頂面加熱）Fig.12 The relationship between local Nusselt number and Richardson number (top heated)

圖14為Re數和Ri數之間的影響關系，將圖中的曲線縱向對比可知，相同工況下，Re數越大，Ri數越小。原因在于Re數越大，流體流速越大，混合對流過程中受迫對流的影響越大，自然對流的影響越小，流動過程類型偏向受迫對流，Ri數因此減小。將圖中的去向橫向對比可知，相同入口溫度下，加熱熱流密度越大，Ri數越大，Re數越大；相同加熱熱流密度下，流體入口溫度越高，Re數越大，Ri數越小。原因在于非均勻加熱熱流密度越大，浮升力效應越明顯，混合對流過程強度越大，Ri數越大，同時熔鹽物性參數隨溫度變化而變化，對Re數產生影響。而流體入口溫度越大，流體與加熱壁面間的溫度差就會越小，進而浮升力效應所帶來的影響變小，Ri數變小。

2.5 壁面導熱對混合對流過程的影響

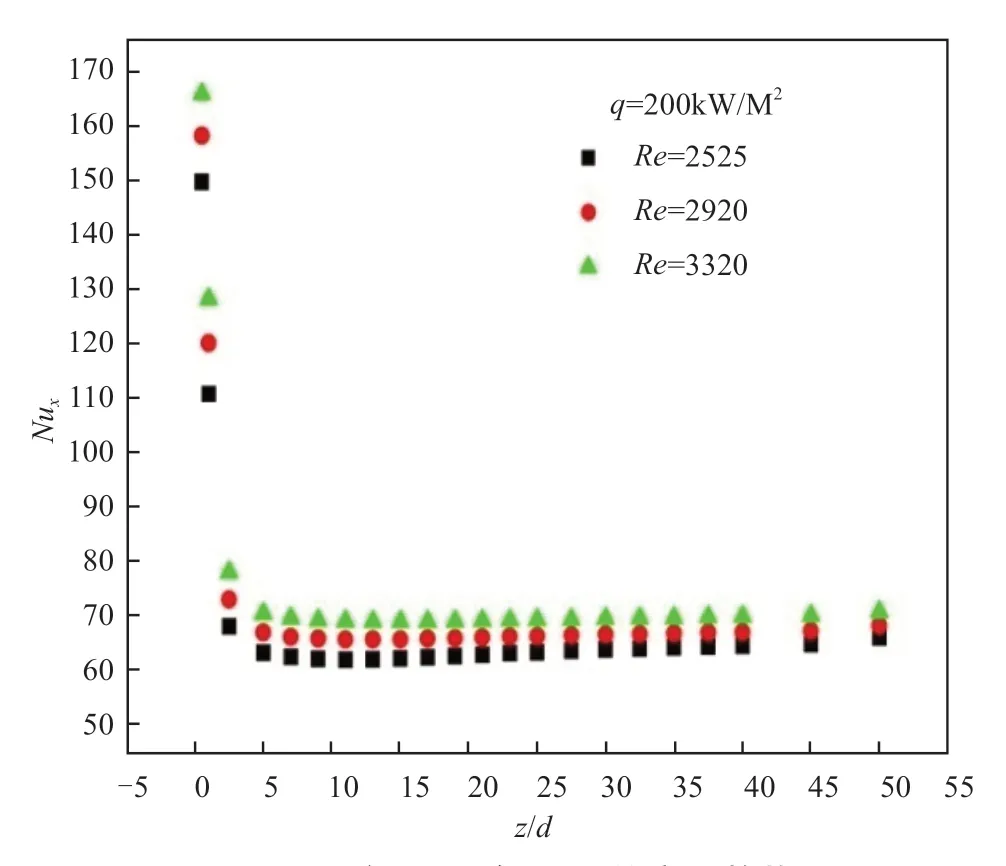
圖13 局部Nux隨Re數的變化趨勢Fig.13 Changes of local Nusselt varied with z/d under different Reynold number

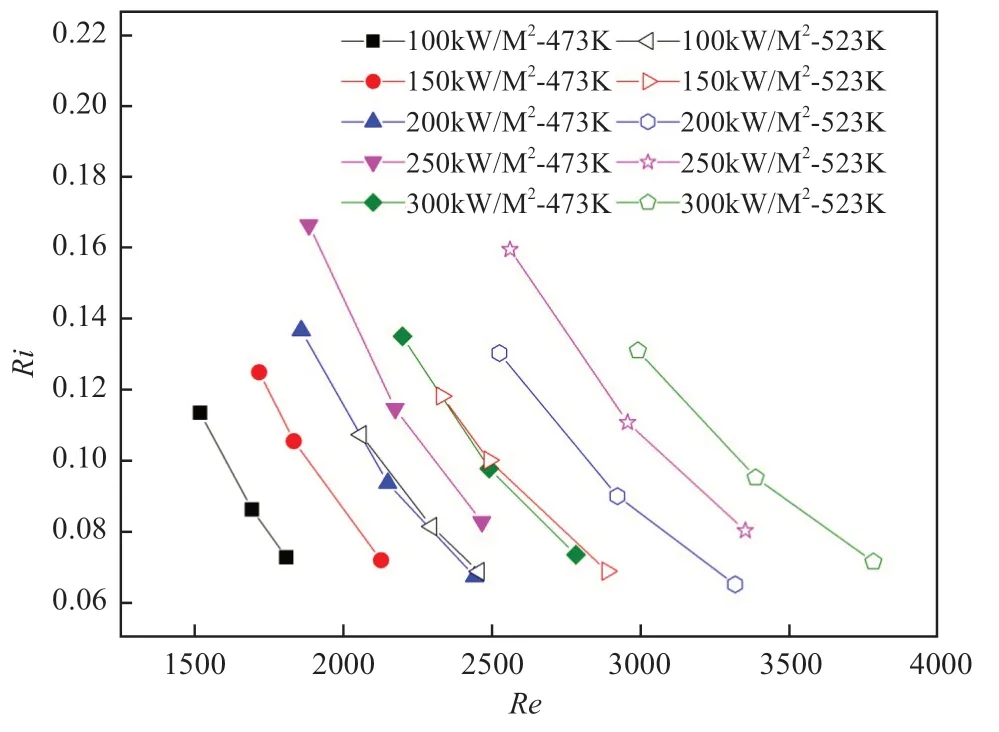
圖14 Ri數與Re數間的變化關系Fig.14 The relationship between Richardson number and Reynold number

圖15描述了壁面導熱對局部Nux的影響關系。從圖中可看出考慮壁面結果與不考慮壁面導熱結果[15-16]所得出的規律基本一致，側面加熱情況所體現出的傳熱能力最強，頂面加熱結果最弱。原因是由于各加熱方式產生了不同數量和不同規格的渦流，渦流的存在對傳熱過程產生了影響。與不考慮壁面導熱結果相比不同之處在于考慮壁面導熱結果的局部Nux均高于忽略壁面導熱的計算結果；且考慮壁面導熱的計算結果局部Nux回升的位置均要早于忽略壁面導熱的結算結果。這是因為壁面導熱的存在使得溫度分布更加均勻，入口段熱量的堆積造成壁面溫度與流體溫度的溫差低于忽略壁面導熱的結果，從而使得局部Nux更高，增強了換熱效果,進而局部Nux的最小值位置更加提前。

3 結 論

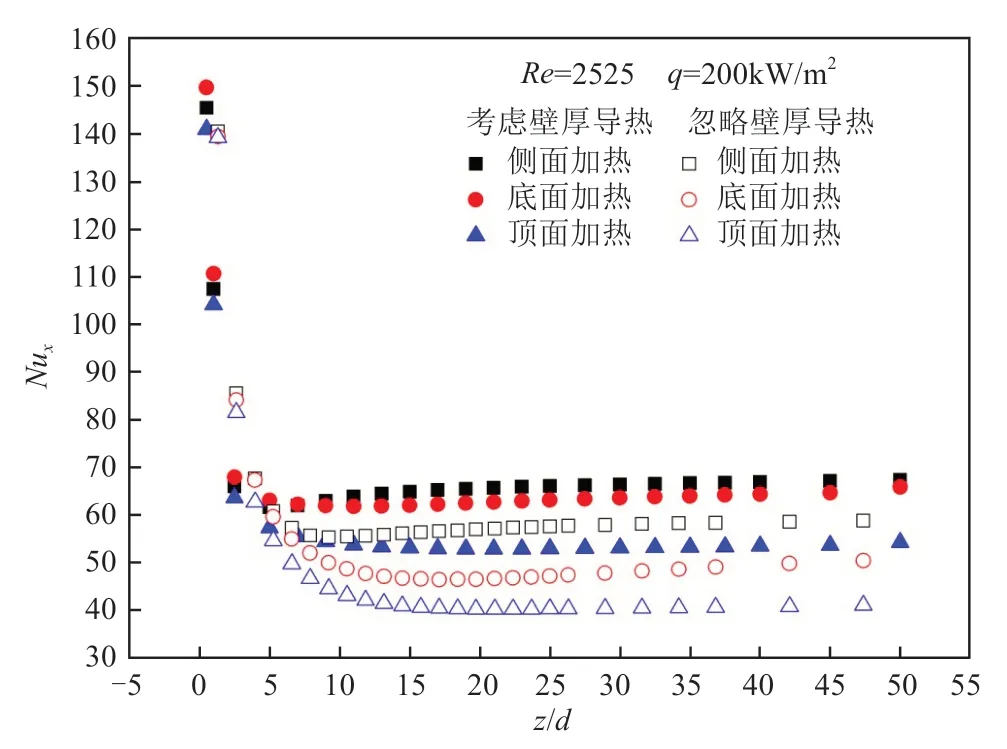
圖15 壁面導熱對局部Nux隨無量綱量y/d變化趨勢的影響（Re2525）Fig.15 Influence of tube wall heat conduction on local Nusselt number（Re2525）

本文研究了考慮壁面導熱影響的水平方管內的熔鹽混合對流傳熱過程。基于數值模擬方法對單面加熱情況下熔鹽混合對流的流動特性和傳熱特性進行了計算與分析，得到了考慮壁面導熱影響下熔鹽單面加熱情況下混合對流傳熱特性，進一步討論無量綱參數間的變化關系，并將結果與流型判定圖和經典關聯式進行對比，可得出如下結論：混合對流傳熱中存在的浮生力使核心區形狀發生改變，核心區與加熱面貼近。考慮管壁導熱，主流核心區形狀更加均勻，局部Nux更高且回升位置更加提前，Nu數隨Re數、Ri數的增大而增大，局部Nux數隨流動距離的深入先減小后增大。基于混合對流判定準則驗證得到數值模擬結果位于湍流混合對流區