巧構造 妙解題
——中考復習之一道質檢題的教學思考

福建省泉州外國語學校 黃全偉

臨近中考，各地質檢紛至沓來，質檢卷在揣摩中考動向的同時，也在考前比較好地做了查缺補漏。著名數學家波利亞指出：試著解決一個容易著手的簡單問題、特殊的問題、類似的問題。卷子多了，時間少了，自然需要對卷子、對題目做出篩選，在復習的時候做到舉一反三，滲透思想方法尤為重要，基于對平時所學知識的拓展和延伸，無論在學習能力和解題能力上，再上一個臺階。本文即選取一道質檢題為載體，充分發揮學生主觀能動性，并適時交流，如何巧思構造，妙解題型。

一、回顧試題

如圖1，在矩形ABCD 中，對角線AC、BD 相交于點O，E 是邊AD 的中點，且DC=1。

（1）求證：AB=DE；

（2）求tan ∠EBD 的值。學生剛參加完市質檢，對題目的熟悉度較高，熱情度較高，本題立足基本求線段長度的方法，構造直角三角形求銳角三角函數。適合用來復習鞏固與提高。

二、展示問題（2）各種解法

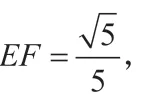
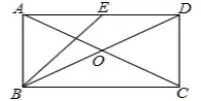
圖1

作高構造直角三角形，有高的地方可想起用面積法，面積法可求出所需條件EF 的長。

解法二：如圖3，過點D 作DF ⊥BE 的延長線于點F，與解法一同理，利用△BDE面積求出DF，利用勾股定理求出即可求出的值。

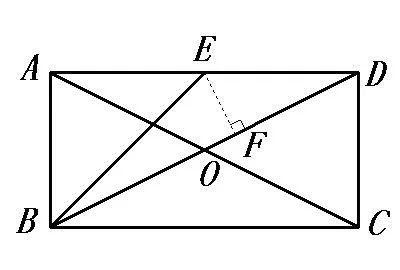
圖2

高不一定作在三角形內部，鈍角三角形的高亦可作在外部，學生能想到此法，應給予充分肯定，善于利用高構造面積法。解法充分體現了面積法的一個基本技巧，即用兩種或兩種以上的方法表示同一個圖形的面積，進而通過面積等式找出所求量之間的關系，或求出需要的量。

解法三：如圖4，連接CE 交BD 于點F，易證△BCE 是等腰直角三角形，∠BEF=90°，由勾股定理求出CE，由△DEF ∽△BCF 可求出EF，即可求出的值。

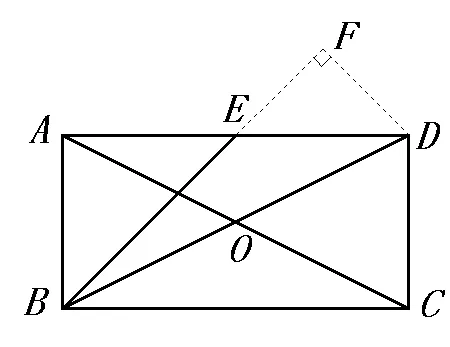
圖3

圖4

直角三角形是最常見的三角形，在歷年中考題中都有直角三角形的身影，最常見的可數直角三角形三角函數的實際應用。有些是明顯存在直角三角形，有些是根據已知條件隱藏著直角三角形，只需簡單作輔助線。

利用現有圖形特征，直接連接EC，構造等腰直角三角形，利用相似，此法輔助線簡單，善于觀察，充分利用已知條件。

和角公式作為初中數學知識的課外補充，學生在理解公式由來基礎上，能用公式求角度正切值，不需要作輔助線，為高中學習奠定基礎。

解法五：如圖5，以點B 為原點，邊BC 所在直線為x 軸建立平面直角坐標系，可知點E、B、D 的坐標，求出直線BD 的函數關系式，利用點到直線距離公式求出點E 到直線BD 的距離EF，圖5勾股定理求出BF，即可求出的值。

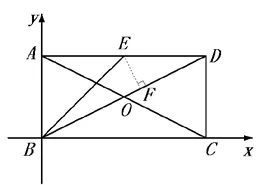
圖5

建立平面直角坐標系，并非對每道幾何題都適用、好用，但有了此種思維方式，在需要的時候，可以達到優化解題目的。

各種解法展示，讓學生體驗不同方法，發散思維，多角度解題思路，增強自主歸納能力。

以上方法均為構造直角三角形，同學們是否可以考慮轉化銳角∠EBD，將它轉化到一個直角三角形中來求正切值呢？

引導：∠EBD 可以看作是定線段DE 所對的張角，定線段DE 是否可以對其他與之相等的張角呢？

生：可以構造圓。利用“在同圓或等圓中，同弧所對的圓周角相等，都等于所對圓心角的一半”。

如圖6，可以將∠EBD 轉化到∠EFD，而∠EFD=90°，△DEF 是直角三角形。

換角度思考，不一定只局限于構造直角三角形，可以利用定線段所對張角相等，通過構造輔助圓把角轉化。

三、拓展提高

問 題（3）：如 圖6，以 點B 為 原點，邊BC 所在直線為x 軸建立平面直角坐標系，在坐標軸上是否存在點M，使得tan ∠DME 與（2）中求得的值相等？若存在，請求出點M 的坐標，若不存在，請說明理由。

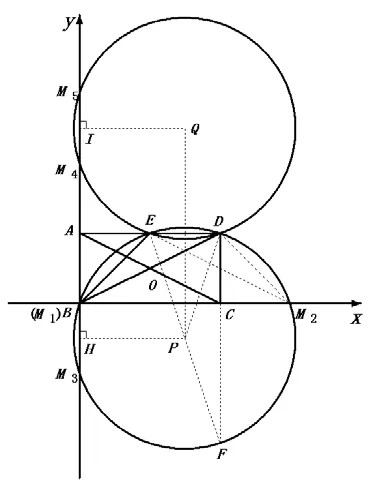
圖6

角是幾何圖形中最重要的元素，而圓的特征賦予角極強的活性，使得角能靈活地互相轉化。根據圓心角與圓周角的倍半關系，可實現圓心角與圓周角的轉化；由同弧或等弧所對的圓周角相等，可將圓周角在大小不變的情況下，改變頂點在圓上的位置進行探索；由圓內接四邊形的對角互補和外角等于內對角，可將與圓有關的角互相聯系起來。

轉化角在此類問題中，能起到化隱為顯、化難為易的解題效果。不僅可以構造直角三角形來求銳角三角函數，還可以構造輔助圓，利用“在同圓或等圓中，同弧所對的圓周角相等，都等于所對圓心角的一半”，將銳角轉化，達到化難為易的解題效果。

構造輔助圓巧解中考壓軸題關于動點對定線段所張的角為定值問題，從表面看似與圓無關，但如果我們能深入挖掘題目中的隱含條件，善于聯想所學定理，巧妙地構造符合題意特征的輔助圓，再利用圓的有關性質來解決問題，往往能起到化隱為顯、化難為易的解題效果，還考查了學生的創造性思維，有利于培養學生分析問題的能力。這里，構造輔助圓實則成了解題的關鍵。