初中數(shù)學(xué)勾股定理的多種證明方法

江西省南昌市廣南學(xué)校 劉 瑩

引領(lǐng)學(xué)生探索多種證明勾股定理的方法，對(duì)扎實(shí)學(xué)生數(shù)學(xué)基礎(chǔ)知識(shí)、提高學(xué)生解決問題的能力具有重要作用。本文從以下幾點(diǎn)闡述初中數(shù)學(xué)教學(xué)中如何引導(dǎo)學(xué)生從多角度探索勾股定理的證明方法。

一、平移推理法

平移推理法簡單有趣，有助于學(xué)生的理解記憶。在學(xué)生初次接觸勾股定理時(shí)，教師不妨引導(dǎo)學(xué)生使用平移法證明勾股定理，以此激發(fā)學(xué)生的學(xué)習(xí)興趣。

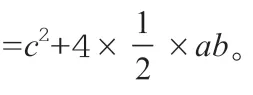
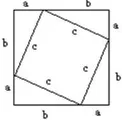
圖1

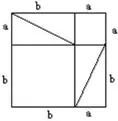
圖2

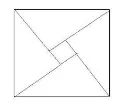
圖3

二、割補(bǔ)拼接法

割補(bǔ)拼接法證明方法變化多，對(duì)鍛煉學(xué)生思維的靈活性、獨(dú)創(chuàng)性和敏捷性具有一定的作用。因此教師便可引導(dǎo)學(xué)生利用割補(bǔ)拼接法證明勾股定理，以提高學(xué)生的思維能力。

首先，我讓學(xué)生準(zhǔn)備若干正方形和直角三角形的卡片，讓學(xué)生自由拼接出其他圖形，試圖找出其中勾股定理的證明方法。待學(xué)生思考一陣，我便用多媒體為學(xué)生展示上圖3，并介紹道：“這是我國古代數(shù)學(xué)家趙爽創(chuàng)制的‘勾股圓方圖’，他利用這幅圖證明了勾股定理，同學(xué)們能發(fā)現(xiàn)這幅圖的奧妙嗎？”我讓學(xué)生利用手邊的卡片拼出“趙爽弦圖”，并提示學(xué)生：“設(shè)圖中直角三角形的兩條直角邊長分別為a、b（b>a），斜邊長為c，那么這個(gè)大正方形的面積有幾種表示方法呢？”在我的引導(dǎo)下，一名學(xué)生寫出證明過程：

大正方形的邊長為c，其面積為c2。

因?yàn)閳D中四個(gè)直角三角形全等，

所以小正方形的邊長為b-a，其面積為（b-a）2。

然后，我再鼓勵(lì)學(xué)生拼出其他圖形并進(jìn)行證明。通過這一過程，可以讓學(xué)生了解到多種證明勾股定理的渠道，并有效鍛煉學(xué)生的思維品質(zhì)，培養(yǎng)學(xué)生的創(chuàng)新能力，從而提升學(xué)生的數(shù)學(xué)綜合素養(yǎng)。

三、圓形輔助法

以上證明勾股定理的方法都離不開正方形的輔助，為拓展學(xué)生思維，我又引入“圓形輔助法”，即通過作直角三角形的外接圓、內(nèi)切圓來證明勾股定理。這種方法涉及一些圓的知識(shí)，但并不復(fù)雜，可作為勾股定理的拓展學(xué)習(xí)。且由于這種證明方法較為新穎，可以有效激發(fā)學(xué)生的探索欲望，教師也可以借此鍛煉學(xué)生自主探究的能力。

首先，我利用多媒體為學(xué)生展示圖4，并做簡單介紹：在Rt △ABC 中，直角邊BC=a，AC=b，斜邊AB=c。作△ABC 的內(nèi)切圓，切點(diǎn)為D、E、F，半徑為r。

然后我向?qū)W生說明“過切點(diǎn)的半徑垂直于該切線”的性質(zhì)，接著便讓學(xué)生自主探究勾股定理的證明方式。結(jié)果，學(xué)生便根據(jù)三角形全等的性質(zhì)，找出圖中幾組長度相等的邊，得出AC+BCAB=2r，即a+b-c=2r，進(jìn)而得出a2+b2+2ab=4（r2+rc）+c2。然后，又將△AOC、△AOB、△BOC 的面積相加，得出△ABC 的面積為r2+rc。又因?yàn)樗杂蒩2+b2+2ab=4（r2+rc）+c2可以得出a2+b2=c2。

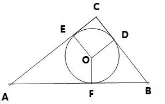
圖4

學(xué)生先是利用圓的性質(zhì)和全等三角形的知識(shí)找出有價(jià)值的條件，然后根據(jù)以往證明思路找出計(jì)算大三角形面積的兩種方法，并找出等量關(guān)系，進(jìn)而證明了勾股定理。所以說這種證明方法對(duì)于開拓學(xué)生思維、鍛煉學(xué)生探究能力大有裨益。

總之，在初中數(shù)學(xué)勾股定理的教學(xué)中，教師可適當(dāng)為學(xué)生介紹多種勾股定理的證明方法，以激發(fā)學(xué)生的學(xué)習(xí)興趣和學(xué)習(xí)潛能，開拓思維，進(jìn)而提升學(xué)生的數(shù)學(xué)綜合能力。