高中數(shù)學(xué)“圓錐曲線最值與范圍問題”的復(fù)習(xí)策略
河南省固始縣慈濟(jì)高級中學(xué)高二(38)班 王曉萱
圓錐曲線問題的考查題目類型較多,考查內(nèi)容較廣,如果試題再與函數(shù)、不等式等知識點(diǎn)融合,這就大大提升了試題難度,使得我們高中生在解題中很難順利解答,這也正是備受高考命題人青睞的原因。圓錐曲線是高考的主干知識之一,既占有較大分量,又有一定的難度。圓錐曲線中的最值問題也是高考試卷中的常考問題,由于所涉及的知識面較為廣泛,所以也是我們高中生感覺較為棘手的一個難點(diǎn)。有鑒于此,我從基礎(chǔ)和拓展兩個方面展開探討,希望對大家有所幫助。
一、重視基礎(chǔ),穩(wěn)拿分?jǐn)?shù)
圓錐曲線問題涉及的知識點(diǎn)多,如果任何一方面出現(xiàn)問題就會導(dǎo)致不必要的失分,由此可知基礎(chǔ)的重要性。數(shù)學(xué)知識體系環(huán)環(huán)相扣,沒有基礎(chǔ)就會錯誤百出,如果題干稍做變動就可能丟分。我在復(fù)習(xí)過程中先夯實基礎(chǔ),通過基礎(chǔ)題找到自身不足、彌補(bǔ)漏洞,穩(wěn)拿基礎(chǔ)題目分?jǐn)?shù),為后面的加大難度做好準(zhǔn)備。
在平面直角坐標(biāo)系xOy 中,P 是雙曲線x2-y2=1 右支上的一個動點(diǎn),若點(diǎn)P 到直線x-y+1=0 的距離大于c 恒成立,則實數(shù)c 的最大值為_____。
解析:本題是一道簡單試題。雙曲線x2-y2=1 是等軸雙曲線,直線x-y+1=0 與一條漸近線y=x 平行。那么,我們可以畫出簡單圖形,運(yùn)用數(shù)形結(jié)合的思想,得到雙曲線右支上的點(diǎn)到直線x-y+1=0 的距離都大于x-y+1=0 與y=x 的距離,因此實數(shù)c 的最大值為
如果我們不擅長運(yùn)用數(shù)形結(jié)合思想解題,那么計算過程就會稍顯復(fù)雜。
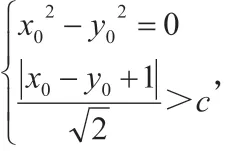
二、注重拓展,分類解答
能力的提升有賴于知識的拓展,因此,在數(shù)學(xué)解題過程中,我與同學(xué)進(jìn)行深入探討,將圓錐曲線類問題進(jìn)行歸類,分為以下兩類數(shù)學(xué)題目類型。在此基礎(chǔ)上,我內(nèi)心非常重視與其他知識的結(jié)合,運(yùn)用數(shù)學(xué)思想來達(dá)到順利解題的目標(biāo)。在練習(xí)圓錐曲線類試題時,題目解答過程難度較大,遇到不懂的問題會與教師或同伴討論,找到問題背后的解法,從而達(dá)到順利解題的目的。
1.有關(guān)長度或面積的最值或取值范圍問題
解析:這是一道關(guān)于圓錐曲線的范圍試題,本題需要用到判別式法來求解。
Δ=16p2-16pb >0,所以p >b。
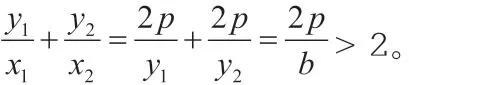
2.圓錐曲線中有關(guān)的幾何元素的最值或取值范圍問題
已知F 為拋物線y2=x 的焦點(diǎn),點(diǎn)A,B 在該拋物線上且位于x 軸的兩側(cè),(其中O 為坐標(biāo)原點(diǎn)),則△ABO 與△AFO 面積之和的最小值為( )。
解析:這是一道圓錐曲線關(guān)于面積的取最值問題,本題有多種解法。
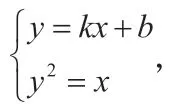
此時直線AB 的方程為y=k(x-2),恒過定點(diǎn)(2,0)。
此外,解法2:設(shè)直線AB 與x 軸的交點(diǎn)為M(m,0),設(shè)直線AB 的方程為x=ty+m,再進(jìn)一步求解。
解法3:本題還可以不再引入新參數(shù)去另設(shè)直線AB 的方程,而是直接用設(shè)的點(diǎn)A(x1,y1),B(x2,y2)求出直線AB,也可以求解得出。
根據(jù)以上分析,我們只要緊緊抓住圓錐曲線的定義,充分運(yùn)用數(shù)形結(jié)合、函數(shù)與方程、化歸轉(zhuǎn)化等數(shù)學(xué)思想,那么圓錐曲線最值與范圍問題就并非無跡可尋。總之,我會在鞏固基礎(chǔ)知識后,努力提升自身解題能力,與他人共同研究分析遇到的難題,多多積累完成數(shù)學(xué)題的經(jīng)驗,從而在考場上盡量拿更多的分?jǐn)?shù)。

