定積分在極限中的應用

（安徽信息工程學院，蕪湖 241000）

引 言

極限內容是高等數學重難點之一，而關于極限的和式極限，往往不太容易得出結果，這對于學過定積分的人來說或許是個優勢，就是將和化成積分，而一般教材中沒有對此內容進行單獨講解，而考研或者競賽中往往會涉及到此類問題，一些基礎薄弱的學生，很難從和化定積分方面，來求解該類極限。本文將從簡單的例子逐步分析，方便讀者掌握。

一、區間n等分的極限化定積分

（1）首先回顧下定積分定義，設f為區間[a，b]上的連續函數，若f恒大于0，在[a，b]上取（n-1）個分點，記為 a=x0＜x0＜x1＜…＜xn=b，此時區間被分成 n 個小區間 [xi-1，xi]i=（1，2……n），為第i個矩形面積，將所有矩形面積作和式，，q=max｛△xi｝，則，若取a=0，b=1，給區間進行n等份，則。

（2）可化為定積分極限題型

①直接對和式極限進行轉化。

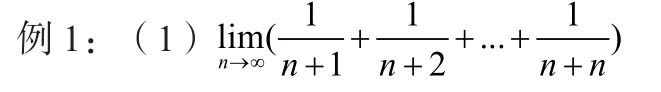
分析：若用學過的知識求解，例如極限定義，顯然這邊有無窮多項不太適合；利用放縮法則也不好對整體進行代換，洛必達更行不通。這時候用定積分定義恰巧可以解決問題。

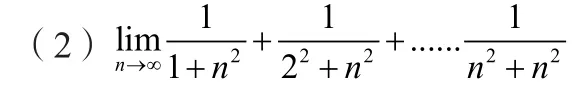
②改寫原極限成和式。

母親在我面前替父親說好話。母親說起那年那場大雪，父親原是準備坐輪船去上海的，卻得到我患病的口信，連夜往家趕。路上用他最鐘愛的口琴換了兩只橘子帶給我。大雪漫天，沒有可搭乘的車輛，他就一路跑著。過了江，好不容易攔下一輛裝煤的卡車……

分析：該題看上去與和式極限沒關聯，但是一般情況下，得要進行變換，使得它成為和式極限。

首先還是改寫極限將原式變形：

分析：我們步驟模仿（1）問進行解題即可。具體步驟如下所示：

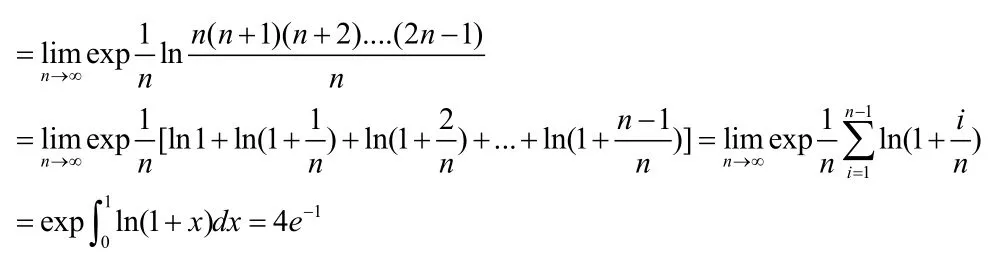
該類題型稍微進行了一點變換，但最終還是用定積分定義巧妙解決。

③基于兩邊夾法則改寫和式

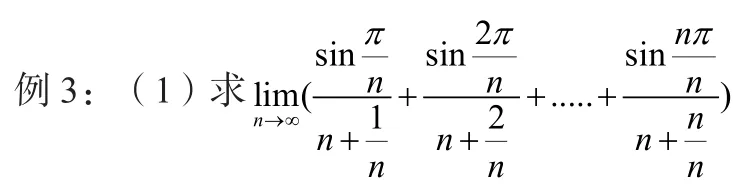
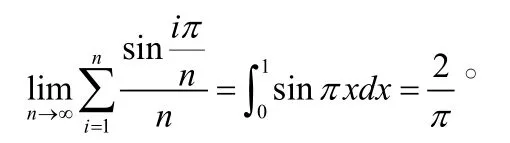
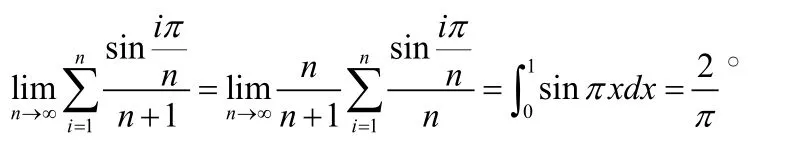
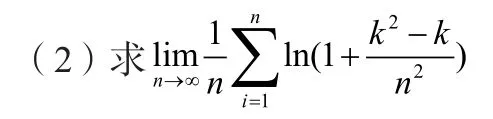
分析：該極限和上述類型相同，已經是和式，也很難找出λi，這時候我們仿照前一題用放縮準則，來進行兩邊夾，從而可以取到λi。

首先觀察極限形式可以直接看出

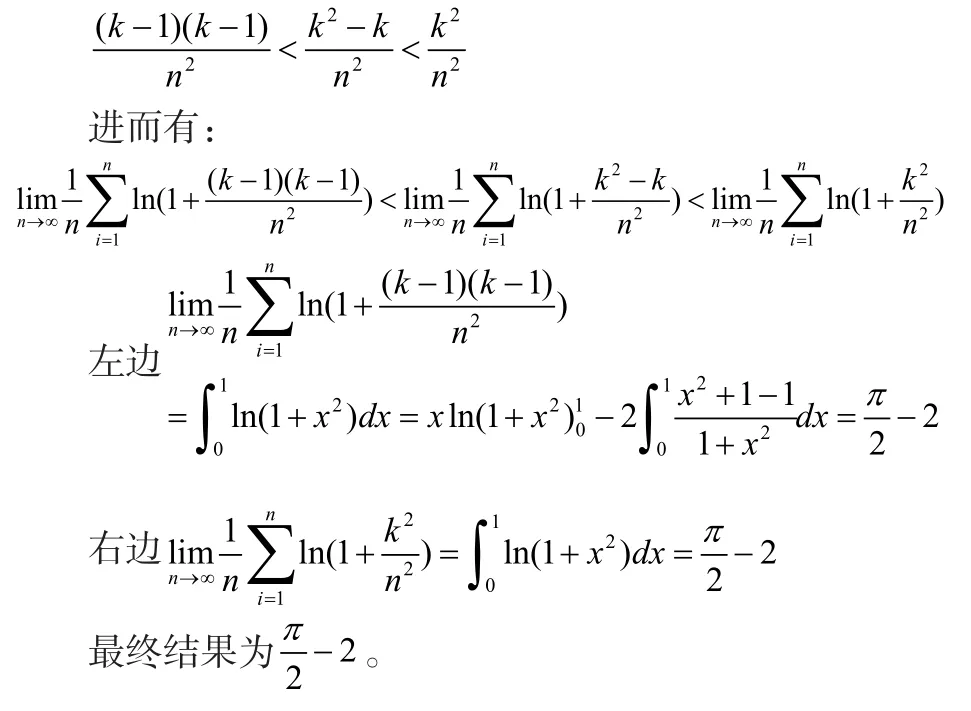
二、非n等份的極限化積分

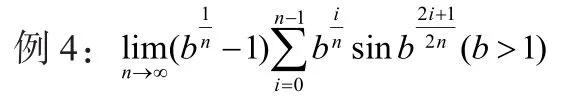
分析：這里的和式如果看成（0，1）區間的n等份的話，不太容易計算，這里的和式，可以看成函數sinx在[1，b]按分劃所作的積分和。

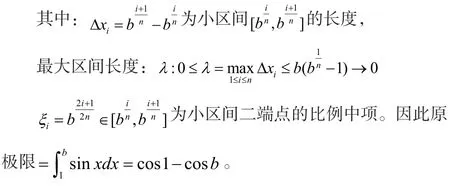
結 語

一般情況下，我們只需要了解并掌握好，n等分的極限化積分情況即可。最后一種情況超過考研范圍。感興趣的讀者可自行研究。