變革數學教學理念 調動學生自主思維

周民強

(臨泉縣長官鎮第一小學 安徽阜陽 236400)

21世紀是一個飛速發展的信息時代，同時也是一個知識爆炸的時代，互聯網在帶來極大便利的同時，也帶來了更加激烈的挑戰。而信息技術的核心層面是數學技術，迎接知識經濟挑戰的重任，也需要強大的數學能力去承擔。

近些年來，盡管中國在國際奧林匹克數學競賽中屢創佳績，但這并不代表中國學生的數學普遍很強，更不代表中國的數學技術已走到世界前列。小學數學作為數學教育中的啟蒙階段，是數學理念與邏輯初步建立的過程，這個過程對于提高學生的數學學習興趣與思維能力至關重要。

在教育理念上，如何根據學生的不同學習背景、水平狀況與心理特征，創造適合數學學習的情景，使學生積極參與到數學學習中，調動學生自主思維，使其主動去汲取知識，以達到教學目的，是擺在每位數學教師面前的一項重要任務。下面，筆者結合多年的小學數學教學的實踐與經驗，談談自身的一些教育體會。

一、注重學習目的教育，端正學生學習動機

多年來，應試教育觀念深入人心，這在短期內可能會帶來一些成績的提升，但是這個學習過程將對學生產生深遠的影響。在小學數學教學中，老師需要結合實際情況，利用各種機會，間斷地進行數學學習的重要性教育，使學生明確數學學習的實際社會意義，看到數學的實際應用價值，激發學生數學學習熱情。

明確其學習目的，端正其學習動機，對于學生數學學習的理解與接受十分重要。課堂數學教學中，教師要闡明教學意義和重要性，結合生活實例，如生活中的購物計算價格，讓學生切實感到生活中的數學存在，直觀發現數學的重要性，端正學生學習態度。

在小學數學的學習中，慢慢明確數學的意義，通過個人的切身實踐，體會到理論知識在實踐生活中的應用，在探索神奇的數學世界中產生興趣，能有效提高數學學習的熱情，并在以后學習中保持積極進取的態度，獲得優良的成績。

二、加強教學理念傳遞，滲透數學思想方法

小學數學教育，是數學學習的入門與啟蒙，與基礎知識相比，數學思想與數學理念的傳遞與滲透對于學生日后的學習更加重要。在數學教學中，教師應重視學生邏輯培養，并盡力展現數學思維過程，促使他們學會問題模式的辨識，并引導其建立必要的數學模型思維過程。

1.設置問題情境，激發學生思維

理論知識結合實踐應用，才是數學學習中的學科優勢。在教學工作中，設置合理數學問題情境，引導激發學生的自主思維，學生產生了求知欲，教學自然事半功倍。例如教學“速度單位的基本了解”這一節，進入正式內容前，我先給學生講了一個小故事：孫悟空和豬八戒比誰飛得快，悟空說：“我一分鐘能飛越十萬八千里。”八戒卻說：“我一秒鐘能飛三萬六千米。”他二人爭執不休，一起去找師傅評理。通過故事引入教學內容，學生帶著濃厚的求知欲和興趣聽完了這節課，教學效果非常好。

傳統文化中隱藏著中華精神和靈魂。隨著國學的普及和發展，傳統文化的價值日益被現代中國人所接受和認可。語文教學中滲透傳統文化，可以提升學生的道德品質和民族自豪感，有助于身心的修養和完善，并幫助學生樹立中國人特有的認識世界和理解世界的觀念，做一名熱愛祖國熱愛人民的好學生。

2.暴露思維過程，發展直覺思維

在小學數學教學中，充分暴露思維過程是重要的指導原則，簡稱為過程性原則。我們小學數學教師應把握過程性原則，創造性地設計具體教學內容，最終課堂上才可能充分展現數學思想，使學生知其然也知其所以然，避免了照本宣科，最大限度地激發學習的主動積極性。直覺思維是指人腦對于對象的本質、規律的直觀感受、領悟和估判，同時也是應用經驗知識對問題進行迅速分析和推理，得到解決問題的方向、方法、途徑和答案的一種思維形式。直覺思維方式使解答過程另辟蹊徑，體現出極大的創造性與顯著效率。

例如下面的這道四則混合運算題：

三、合理組織多向練習，科學發散思維訓練

學生的發散思維與其創造力直接相關，是創造性思維的關鍵所在。而發散性思維主要是指思維的獨創性、靈活性和廣闊性。數學中的一題多答、一題多問、一題多變以及一題多解等多向性練習是鍛煉發散性思維的有效途徑。

1.組織多向性訓練，使學生靈活善思

在小學數學教學中，教師組織多向性思維訓練，并不意味著只追求“多”，更重要的是鍛煉學生多思，在多個方向的問題中積極引導學生把發散產生的東西進行分析比較，及時總結分析。

思考過程：

(1)把職工總數看作單位“1”。

(2)把男職工人數看作單位“1”。

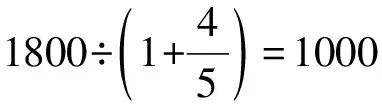
1800-1000=800(人) (女職工人數)

(3)把女職工人數看作單位“1”。

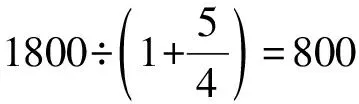
1800-800=1000(人) (男職工人數)

如此分析，既打破了許多學生總是以“總數”為單位“1”的思維定式，又利于學生進行思維訓練。這種引導得當的教學，多向地解決問題，鞏固了基礎知識，也為形成創造性思維打下了基礎。

2.巧妙設立開放題，鍛煉思維獨創性

目前我們所運用的教科書中的練習題，封閉式的占了大多數，少數具有探索性的題目在教師的一再提醒下，避免了錯誤同時，也變成半封閉式的題目，不僅不能發揮出學生的探索能力，更沒法鍛煉他們的思維獨創性。因此，我在實際數學教學中，會特定地拋出一些開放性的題目，供學生思考、討論并分析總結，給他們鍛煉思維提供機會。

例如：設A、B、C三城在一條路程上，一輛貨車以45 km/h的速度由A開往B，一輛汽車以50 km/h的速度由C開往B，4小時后兩車同時抵達B，請問AC之間的路程是多少？

由于本題沒有說明B是否在A與C之間，因此答案不唯一。學生經過激烈的思考與討論后，得到了全面的答案：

第一種情況：(45+50)×4=380(km)

第二種情況：(50-45)×4=20(km)

與結論固定的封閉性問題相比，開放題的解答，要求學生一定要進行思考、判斷、比較、歸納，顯然更有利于鍛煉學生的思維創造性。

3.培養主體意識，提高自學能力

培養學生的獨立思考和自學能力，是數學教學中的一項任務。當前在“應試”教育下，多數學校和老師一般僅重視灌輸學生知識，卻忽視了學生的主體意識和自學能力的培養。

古人云：“授人以魚”不如“授人以漁。”在具體數學教學中，應采用多種教學方式，培養學生主體意識，同時給學生足夠的學習自主權，改變“教師講，學生聽”的傳統教學模式，讓學生由“學會”變成“會學”。例如，對于較高年級的學生，我們可讓他們分組自學，自主備課當老師，課后結合問題一起探討。這樣教學效果非常明顯，學生討論熱情比較高。

在信息技術迅猛發展的時代，掌握了更強大、更先進的數學技術，就搶得了競爭的先機。這迫切需要我們對數學，尤其是對數學教育進行重新審視。小學數學教育作為學生學習生涯中的啟蒙階段，對學生以后的長期學習熱情與積極性的保持和適應未來社會發展至關重要。

若小學數學繼續用傳統方式，則學生很難真正做到學以致用，這會對之后的學習、工作產生不良影響，甚至會讓學生很難應對大數據信息時代的挑戰。因此變革數學教學理念，改變教育方式迫在眉睫。培養學生自學能力，調動學生自主思維，是當前小學教育改革的一項重要任務。