尋找知識背后的道理

王慶菊

[摘 要]課堂應該回歸本質，通過適當的“問題引領”，從根本處追問、從無疑處深究，讓學生從知識的淺表走向內核，并獲得豐富的數學思維和理性體驗，在思辨中感受數學的力量，建立新的思維方式和方法論，尋找知識背后的道理。

[關鍵詞]知識;數理;3的倍數

“3的倍數的特征”是人教版教材五年級下冊第二單元的內容，本節課的重點是讓學生經歷3的倍數的特征的探究過程，掌握3的倍數特征。學生通過列舉、觀察，很容易總結出3的倍數的特征，但教師卻極少或從不引導學生思考其背后的道理，以致學生僅僅知其然而不知其所以然。

追根溯源，打開各種版本的教材可以發現，人教版和北師大版教材都是讓學生在百數圖上圈出3的倍數，然后討論總結其特征;蘇教版教材讓學生在百數圖上圈出3的倍數后，又讓學生在計數器上撥珠表示3的倍數，從而更直觀地發現3的倍數與各個數位上數的和之間的關系;冀教版教材則略去了百數圖，讓學生在數位表上擺小棒，根據所用小棒的根數總結出3的倍數的特征。由此可見，所有版本的教材都對“3的倍數”背后的道理“避而不談”。那么，本節課有沒有必要讓學生知道“為什么”？

M. Kline 在《西方文化中的數學》中指出，數學是一種精神，一種理性精神，正是這種精神，激發、促進、鼓舞人類的物質、道德和社會生活，試圖回答人類自身存在和提出的問題，使人類努力去理解和控制自然，盡力去探索和確立已經獲得知識的最深刻和最完善的內涵。課程不是一種“作為事實”的存在，而是一種“作為關系、過程和價值”的實踐樣式。因此，數學教育不僅要讓學生掌握知識，還要讓學生在自主探究的過程中，思考探究知識背后的數學原理和方法，幫助學生學會思維，使學生想得更清晰、更深入、更全面、更合理，從而提升學生的思維品質，這也是數學教學的價值所在。因此，本節課可在學生總結出“3的倍數的特征”的基礎上，引導學生再往前走一步。

【教學片段】

師：剛才我們已經發現了判斷一個數是不是3的倍數要看各個數位上數的和，對此你有什么問題？

生1：為什么判斷是不是3的倍數要把各個數位上的數加起來？

生2：比如15，15中的“1”表示1個十，“5”表示5個一，為什么在判斷時卻變成了1個一加5個一？明明是1個十，為什么卻成1個一？

師：這是為什么呢？想知道其中的道理嗎？請大家任意寫幾個數，動手分一分、畫一畫，看看這些數為什么是或者不是3的倍數。

學生匯報：

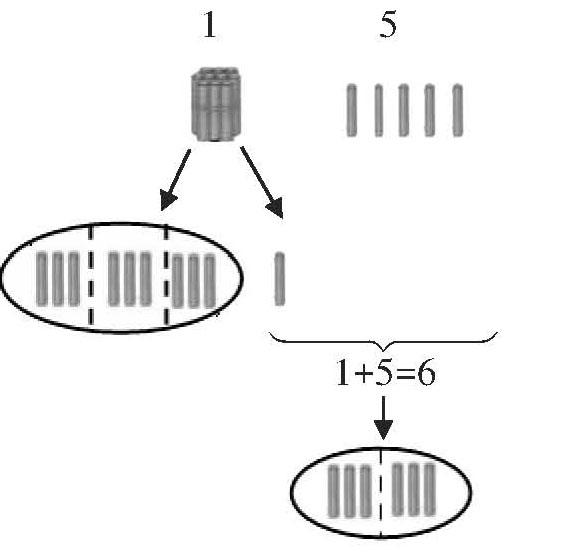
生3（方法一）：我們小組研究的數是15，我們用分小棒的方法進行了研究。15根小棒可以分成10根小棒和5根小棒，先把10根小棒三根三根地分，分3次后還余1根，還有5根小棒，1+5=6，合起來共6根小棒。將6根小棒繼續三根三根地分，正好分完，說明15是3的倍數。

師：你發現了什么？

生3：因為1+5=6，6能被3整除，所以15是3的倍數。

師：一起來看一看，“1+5”中的“1”表示什么？這個“1”從哪來的？

生4：這個“1”表示10除以3的余數，表示余下1根小棒。

師：這個“1”與“15”中的“1”一樣嗎？

生5：不一樣。“15”中的“1”表示1個十，“1+5”中的“1”表示余下來的1個一。

師：為什么要加上5？

生6：加上5是看看現在還剩幾根小棒沒分，繼續三根三根地分，看看能不能正好分完。

師：你們明白判斷15是不是3的倍數，為什么要看“1+5”的道理了嗎？

生7：就是把“1個十”三個三個地分，余1，余下來的1和個位上的“5”合起來再分，如果能分完就是3的倍數，如果不能分完就不是3的倍數。

生8（方法二）：我們小組研究的數是243，我們是用分正方形的方法進行研究的。三個三個地分一百個小正方形，最后余1個;三個三個地分兩百個小正方形，最后余2個;三個三個地分十個小正方形，最后余1個小正方形，三個三個地分四十個小正方形，最后余4個小正方形;連上個位上的3個小正方形，一共還剩2+4+3=9個小正方形。繼續三個三個地分9個小正方形，正好分完，說明243是3的倍數。

師：你能說一說“2+4+3”的道理嗎？

生8：就是把百位上余下的2、十位上余下的4、個位上余下的3合起來，看看是不是3的倍數。

生9（方法三）：我們組研究的數是417，我們是根據數的組成進行研究的。

師：你明白“4+1+7”的道理嗎？

生9：就是把百位、十位、個位上的數除以3之后剩下的數加起來，如果這個和是3的倍數，原來的數就是3的倍數。

師：現在大家明白判斷一個數能否被3整除為什么要看各位上數的和的道理了嗎？

【教學思考】

著名教育學家派珀特講過這樣一個故事：“一個人不擅記花草的名字，他看著一朵花，使勁地想名字，就是想不起來。直到有一天，他換了一種辦法：先從花的名字開始，想為什么這個名字適合這朵花。很快他就能流利地說出各種花的名字。”因此，關于知識，最根本的問題是，我們向知識尋求什么？

1.善學者盡其理

《荀子·大略》有言：“善學者盡其理。” “2、3、5的倍數的特征”屬于數論部分，與“2、5的倍數的特征”相比較，3的倍數的特征更隱蔽，這或許就是幾乎所有的教材對此回避的重要原因。

張卓玉先生曾說，每個學科的教材都存在兩個版本，一個是體現學科知識體系的有形的版本，一個是品質、思想、故事構成的無形的版本。回想以前的課堂，教師總是千方百計引導學生觀察、猜想，總結出3的倍數的特征，而沒有就這一知識進行深層次的追問與探究。這種基于實際情境給出結論的做法，極易讓學生形成“數學知識是由具體實際問題簡單歸納出來的”的認識。好的數學教育，要回到思維原點處，挖掘學科知識背后的學科觀念、思想方法，并在課堂中以恰當的方式傳遞給學生。

上述教學片段中，在“為什么判斷一個數是不是3的倍數要看各個數位上數的和”這個核心問題的引領下，學生通過舉例分析、獨立思考、動手實驗、合作探究，借助小棒圖、方格圖等直觀材料以及數的組成等材料，逐步明白“各個數位上數的和就是各個數位上的數除以3所得余數的和”，從規律的淺表走向內核，探明知識背后的道理，將數學學習引向數學精神、數學理性與數學思想的深處。

2.知識背后有什么？

縱觀人類發展史，任何知識都是特定文化背景下的產物，都蘊含著特定的思想、思維方式和價值觀念，人類認知世界的思維方式、文化價值觀念、文化精神等組成了知識的內核。因此，知識的背后是對符號知識的超越和追問，是對知識所隱含的思想、意義、思維方式的深層追問。

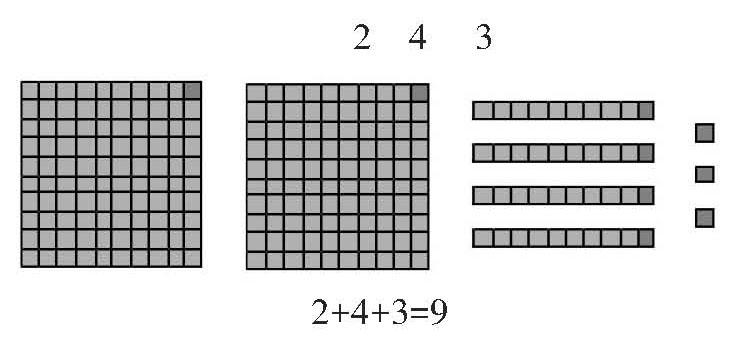
“3的倍數的特征不再只看個位，而要看各個數位上數的和”，盡管書上“你知道嗎？”運用舉例的方法說得非常具體詳盡，可學生就是疑惑不解。究其原因，3的倍數特征的道理涉及了位值概念，而位值概念比較抽象。化抽象為具體最有效的方法就是數形結合。教師只有巧妙地引導學生借用小棒、方格圖等自主探究，直觀地看出判斷15是不是3的倍數時“1+5”中的“1”不是十位上的“1”，而是十位上的“10”除以3所得的余數，即“1根小棒”，這個余數恰好與十位上的數字相同;判斷243是不是3的倍數時“2+4+3”中的“2”、“4”、“3”分別是百位上的“2”、十位上的“4”除以3所得的余數和個位上的“3”，即“百位上是幾，三個三個地分就剩幾;十位上是幾，三個三個地分就剩幾，分完以后剩下的數與數位上的數是一樣的，所以可以把“3的倍數的特征”歸納為“各個數位上數的和是3的倍數”。

知識是一粒種子，具有生長的力量。“拆數再除”化隱為顯，直指問題的本質，把3的倍數特征的道理展現得淋漓盡致，使學生在數學學習中獲得智慧的啟迪、精神的滋養和生長的力量。

（責編 金 鈴）