裝備激勵(lì)約束定價(jià)模式機(jī)理對(duì)比分析與設(shè)計(jì)
吳詩(shī)輝,劉曉東,胡博,賀波
1.空軍工程大學(xué) 裝備管理與無(wú)人機(jī)工程學(xué)院,西安 710051 2.軍事科學(xué)院 評(píng)估論證研究中心,北京 100091
激勵(lì)約束定價(jià)模式是控制裝備成本,調(diào)動(dòng)承包商積極性的一種重要定價(jià)模式[1-2]。美國(guó)國(guó)防部先后修訂《聯(lián)邦采辦條例》及《美軍合同定價(jià)參考指南》[3],頒布了一系列關(guān)于武器系統(tǒng)采辦改革的法律、法規(guī)[4-11],形成了美軍的激勵(lì)約束定價(jià)機(jī)制[12]。2013年以來(lái),我軍也針對(duì)裝備激勵(lì)約束定價(jià)模式開(kāi)展了一定的探索和嘗試[13-14],提出了一種基于固定利潤(rùn)率的成本激勵(lì)約束定價(jià)模式[15],試圖改變當(dāng)前單一的5%固定利潤(rùn)率定價(jià)模式。文獻(xiàn)[14]利用博弈論的思想分析了基于固定利潤(rùn)率的成本激勵(lì)約束定價(jià)模式的規(guī)律,從審價(jià)程度和是否虛報(bào)成本角度出發(fā),分析了軍方采取“一般審價(jià)”和“重點(diǎn)審價(jià)”策略,企業(yè)采取“虛報(bào)成本”和“實(shí)報(bào)成本”策略時(shí),雙方的最優(yōu)策略解,得出了指導(dǎo)性的結(jié)論和建議。文獻(xiàn)[15]認(rèn)為,基于固定利潤(rùn)率的成本激勵(lì)約束定價(jià)模式起到了一定的激勵(lì)約束作用,應(yīng)作為一種過(guò)渡性方案。從現(xiàn)有文獻(xiàn)看,針對(duì)激勵(lì)約束定價(jià)模式的研究主要停留在定性分析層面和簡(jiǎn)單的定量公式介紹[16-18],對(duì)于不同激勵(lì)約束定價(jià)模式的內(nèi)在機(jī)理和控制規(guī)律研究不足,顯然不足以指導(dǎo)我軍的裝備激勵(lì)約束定價(jià)模式改革。基于此,本文針對(duì)美軍的激勵(lì)約束定價(jià)模式和我軍的激勵(lì)約束定價(jià)模式進(jìn)行了分析和比較,研究了2種不同激勵(lì)約束定價(jià)模式的內(nèi)在機(jī)理和控制規(guī)律,并將其與傳統(tǒng)的固定利潤(rùn)率定價(jià)模式[19]進(jìn)行對(duì)比分析,提出了軍方的期望價(jià)格和承包商的期望利潤(rùn)的計(jì)算模型,并給出了制定有效裝備激勵(lì)約束定價(jià)模式的建議。
1 3種定價(jià)模式機(jī)理
為研究問(wèn)題方便,本文將3種定價(jià)模式分別記為定價(jià)模式1~3,如表1所示。其中,定價(jià)模式1表示美軍采用的激勵(lì)約束定價(jià)模式[12,20],定價(jià)模式2表示我軍探索的基于固定利潤(rùn)率的成本激勵(lì)約束定價(jià)模式[13-15],定價(jià)模式3表示我軍傳統(tǒng)的5%固定利潤(rùn)率定價(jià)模式。

表1 3種定價(jià)模式的名稱(chēng)約定Table 1 Abbreviated name for three cost strategies
1.1 定價(jià)模式1
定價(jià)模式1表示美軍采用的激勵(lì)約束定價(jià)模式。假設(shè)軍方在論證階段確定某項(xiàng)目的成本指標(biāo)為:目標(biāo)成本(記為CT)、成本上限(記為CU)和成本下限(記為CD);同時(shí),根據(jù)目標(biāo)成本、成本上限和成本下限,使用結(jié)構(gòu)性的利潤(rùn)分析方法——“加權(quán)準(zhǔn)則法”[12,15],算得項(xiàng)目的3個(gè)利潤(rùn)指標(biāo):目標(biāo)利潤(rùn)(記為PT)、利潤(rùn)上限(記為PU)和利潤(rùn)下限(記為PD)。
假設(shè)實(shí)際成本為CF,這里規(guī)定成本超支時(shí)對(duì)應(yīng)的利潤(rùn)為約束利潤(rùn),成本節(jié)約時(shí)對(duì)應(yīng)的利潤(rùn)為激勵(lì)利潤(rùn),則由激勵(lì)(約束)利潤(rùn)計(jì)算公式,可得
1) 當(dāng)實(shí)際成本超支時(shí),即CF>CT,約束利潤(rùn)PF為
PF=(CT-CF)x+PTCF>CT
(1)
式中:x表示實(shí)際成本超支時(shí)承包商的風(fēng)險(xiǎn)分?jǐn)偙壤?/p>
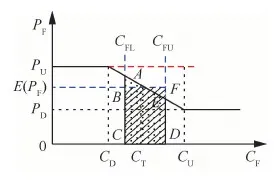
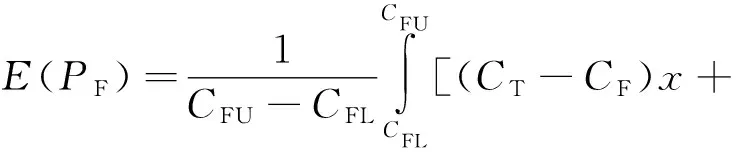
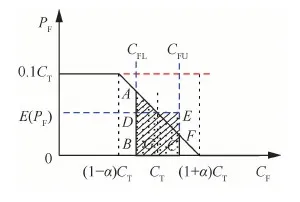
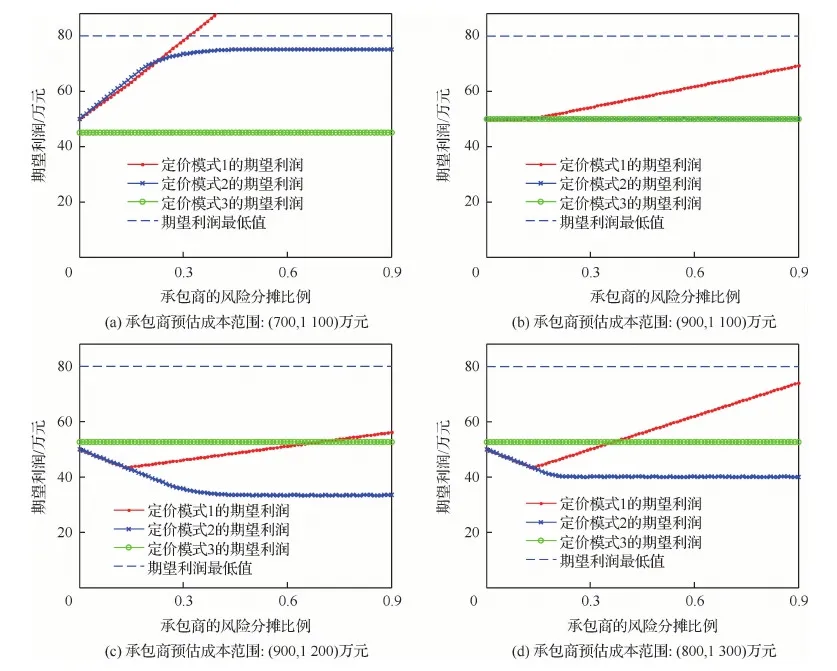
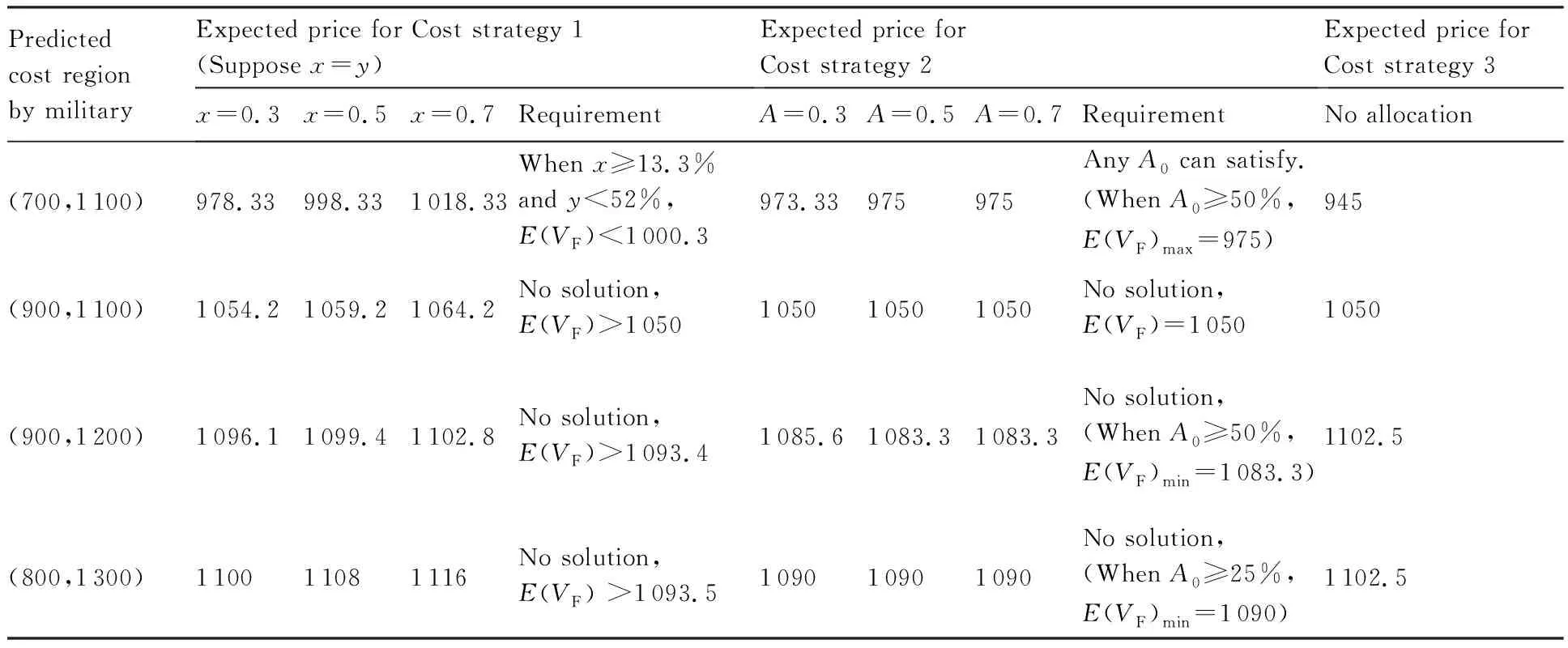
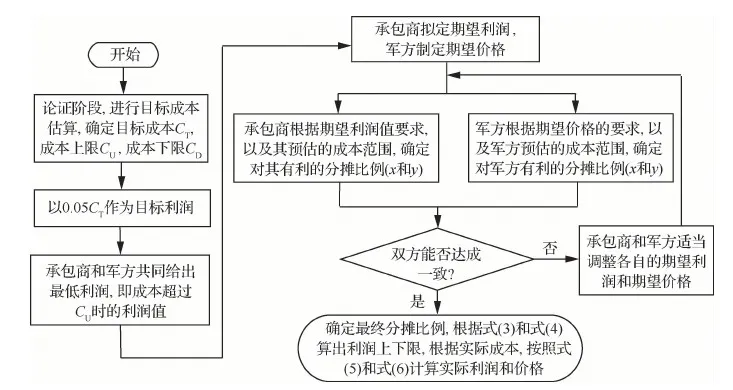
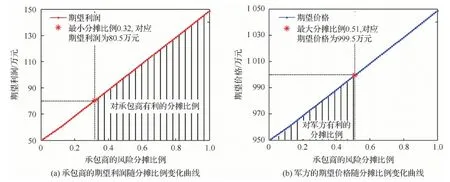
2) 當(dāng)實(shí)際成本節(jié)約時(shí),即CF PF=(CT-CF)y+PTCF (2) 式中:y表示實(shí)際成本節(jié)約時(shí)承包商的風(fēng)險(xiǎn)分?jǐn)偙壤?/p> 根據(jù)激勵(lì)約束定價(jià)策略,x和y應(yīng)滿足以下條件: 1) 當(dāng)實(shí)際成本達(dá)到成本上限時(shí),即CF=CU,此時(shí)的激勵(lì)(約束)利潤(rùn)應(yīng)等于利潤(rùn)下限,即有 PF=PD?(CT-CU)x+PT=PD? (3) 將式(3)代入式(1),得到成本超支時(shí)的激勵(lì)(約束)利潤(rùn)PF為 可以看出,當(dāng)實(shí)際成本超支時(shí),CF越大,則PF越低,利潤(rùn)越低。 2) 當(dāng)實(shí)際成本達(dá)到成本下限時(shí),即CF=CD,此時(shí)的激勵(lì)(約束)利潤(rùn)應(yīng)等于利潤(rùn)上限,即有 PF=PU?(CT-CD)y+PT=PU? (4) 將式(4)代入式(2),得到成本節(jié)約時(shí)的激勵(lì)(約束)利潤(rùn)PF為 可以看出,當(dāng)實(shí)際成本節(jié)約時(shí),CF越小,則PF越大,利潤(rùn)越高。 3) 當(dāng)實(shí)際成本等于目標(biāo)成本時(shí),即CF=CT,激勵(lì)(約束)利潤(rùn)應(yīng)等于目標(biāo)利潤(rùn)。將CF=CT帶入式(1)或式(2),顯然可得到:PF=PT。 綜上,得到激勵(lì)(約束)利潤(rùn)PF的計(jì)算公式為 PF= (5) 則最終價(jià)格為 VF=CF+PF (6) 注意到,式(5)與文獻(xiàn)[12]給出的公式是一致的,這實(shí)際上是解釋了實(shí)際成本超支或節(jié)約時(shí)承包商的風(fēng)險(xiǎn)分?jǐn)偙壤挠?jì)算機(jī)理。 根據(jù)以上分析,可得出以下規(guī)律: 1) 從式(5)和式(6)可以看出,如果實(shí)際成本低于最低成本,價(jià)格等于實(shí)際成本與利潤(rùn)上限之和;如果高于最高成本,價(jià)格等于實(shí)際成本與利潤(rùn)下限之和。 2) 從式(3)和式(4)可以看出,承包商的風(fēng)險(xiǎn)分?jǐn)偙壤c3個(gè)利潤(rùn)指標(biāo)有關(guān),即目標(biāo)利潤(rùn)PT、利潤(rùn)上限PU和利潤(rùn)下限PD。成本超支時(shí),主要與目標(biāo)利潤(rùn)與利潤(rùn)下限的差值PT-PD有關(guān),差值越大,則x越大,承包商需要扣除的超支的懲罰金比例越大,利潤(rùn)越少;成本節(jié)約時(shí),主要與目標(biāo)利潤(rùn)與利潤(rùn)上限的差值PU-PT有關(guān),差值越大,則y越大,承包商能夠分得節(jié)約成本的獎(jiǎng)勵(lì)金越多,利潤(rùn)越多。 3) 從式(3)還可以看出,當(dāng)PD-PT=CT-CU時(shí),意味著承包商將承擔(dān)100%的成本超支風(fēng)險(xiǎn),利潤(rùn)下限值PD應(yīng)不低于CT+PT-CU。 4) 當(dāng)成本分?jǐn)偙壤阎獣r(shí),利潤(rùn)上限PU和利潤(rùn)下限PD可根據(jù)式(3)和式(4)確定。例如,要使得承包商承擔(dān)的超支風(fēng)險(xiǎn)比例為30%,可設(shè)計(jì)PD值為:PT-0.3(CU-CT);要使得承包商的節(jié)約風(fēng)險(xiǎn)比例為30%,可設(shè)計(jì)PU值為:PT+0.3(CT-CD)。 參照美軍的激勵(lì)約束定價(jià)模式,我軍也探索了一種激勵(lì)約束定價(jià)模式-基于固定利潤(rùn)率的成本激勵(lì)約束定價(jià)模式,裝備價(jià)格由定價(jià)成本、激勵(lì)(約束)利潤(rùn)、目標(biāo)利潤(rùn)3部分組成[14]。 假設(shè)某項(xiàng)目的定價(jià)成本為C,PE為激勵(lì)(約束)利潤(rùn),CT為目標(biāo)成本,實(shí)際成本為CF,則由激勵(lì)(約束)利潤(rùn)計(jì)算公式[13],可算得 PE= (7) 式中:α∈(0,1),表示控制成本上下限的參數(shù);A∈(0,1),表示承包商的成本分?jǐn)偙壤珹越大則承包商分?jǐn)偝杀镜娘L(fēng)險(xiǎn)越大,即當(dāng)定價(jià)成本超過(guò)目標(biāo)成本時(shí),承包商承擔(dān)的虧損越大,當(dāng)定價(jià)成本低于目標(biāo)成本時(shí),承包商獲取的利潤(rùn)也越多。 顯然,PE可看做是定價(jià)成本C的函數(shù),要保證分段函數(shù)PE的連續(xù)性,需滿足: 將上述2個(gè)方程進(jìn)行推導(dǎo),得到 可得 α=0.05/A (8) 顯然,這里成本控制的上下限參數(shù)α與承包商的成本分?jǐn)偙壤鼳有關(guān),A越大則α越小,根據(jù)式(7),成本上下限區(qū)間((1-α)CT, (1+α)CT)將變小。 裝備的價(jià)格最終由定價(jià)成本、目標(biāo)利潤(rùn)和激勵(lì)(約束)利潤(rùn)3部分組成: V=C+PE+0.05CT (9) 式中:0.05CT表示目標(biāo)利潤(rùn),從這里可以看出,該定價(jià)模式仍然保留了傳統(tǒng)的5%固定利潤(rùn)率的特征。 此時(shí),承包商的實(shí)際利潤(rùn)為 PF=V-CF 假設(shè)這里的實(shí)際成本和定價(jià)成本相等,即C=CF,則有 PF=V-CF=PE+0.05CT (10) 結(jié)合式(7)和式(10)可以看出,當(dāng)定價(jià)成本低于成本下限時(shí),將得到目標(biāo)成本10%的利潤(rùn)(注意,與實(shí)際成本CF無(wú)關(guān)),反之,當(dāng)定價(jià)成本超過(guò)成本上限時(shí),將得不到任何利潤(rùn)(利潤(rùn)為0)。 如果按照傳統(tǒng)的5%固定利潤(rùn)率定價(jià)模式,則承包商的利潤(rùn)為 PF=1.05C-CF 假設(shè)這里的實(shí)際成本和定價(jià)成本相等,則承包商的利潤(rùn)為 PF=0.05CF (11) 一般來(lái)講,承包商主要關(guān)注的是獲得的利潤(rùn),軍方主要關(guān)注的是裝備的價(jià)格,這里分別給出幾種定價(jià)模式下承包商的期望利潤(rùn),以及軍方的期望價(jià)格。 2.1.1 定價(jià)模式1 從式(5)可以看出,實(shí)際利潤(rùn)PF可看做是實(shí)際成本CF的函數(shù),因此,承包商的期望利潤(rùn)實(shí)質(zhì)等于PF(CF)曲線在承包商預(yù)估的成本區(qū)間上的積分,具體解釋如下。 期望利潤(rùn)應(yīng)等于實(shí)際成本為CFi時(shí)的實(shí)際利潤(rùn)PFi與實(shí)際成本為CFi的概率的累積求和: (12) 式中:N表示將區(qū)間(CFL,CFU)等分為N份,N可設(shè)置為非常大的數(shù);P(CFi)表示實(shí)際成本為CFi的概率。 假設(shè)在項(xiàng)目的成本區(qū)間上每個(gè)成本點(diǎn)發(fā)生的概率均相同,則可令 (13) 式中:dCF表示包含CFi點(diǎn)的等分區(qū)間長(zhǎng)度。 顯然,將式(13)代入式(12),可得 (14) 當(dāng)CFL (15) 對(duì)于x=y這種特殊的情形,式(15)可以進(jìn)一步變形為 圖1 定價(jià)模式1下承包商的期望利潤(rùn)Fig.1 Expected profit for contractor under Cost strategy 1 (16) 從式(16)可以看出: 1) 當(dāng)目標(biāo)成本CT位于區(qū)間(CFL,CFU)的中點(diǎn)時(shí),E(PF)=PT,即期望利潤(rùn)等于目標(biāo)利潤(rùn)。 2) 當(dāng)區(qū)間(CFL,CFU)的中點(diǎn)小于目標(biāo)成本CT時(shí),E(PF)>PT,即期望利潤(rùn)要高于目標(biāo)利潤(rùn)。 3) 當(dāng)區(qū)間(CFL,CFU)的中點(diǎn)大于目標(biāo)成本CT時(shí),E(PF) 當(dāng)然,對(duì)于x≠y,或者條件{CFL 2.1.2 定價(jià)模式2 與定價(jià)模式1類(lèi)似,圖2中以期望利潤(rùn)E(PF)為高的矩形BCED面積(以斜線陰影表示)應(yīng)與梯形部分ABCF面積(以點(diǎn)狀陰影表示)相等。 將式(10)代入式(14): (17) 式中:PE可由式(7)計(jì)算,由于PE為分段函數(shù),因此,E(PF)取決于(CFL,CFU)與成本范圍的關(guān)系。 下面討論一種常見(jiàn)的情形,如圖2所示,當(dāng)CFL 圖2 定價(jià)模式2下承包商的期望利潤(rùn)Fig.2 Expected profit for contractor under Cost strategy 2 (18) 從式(18)可以看出 1) 當(dāng)目標(biāo)成本CT位于區(qū)間(CFL,CFU)的中點(diǎn)時(shí),E(PF)=0.05CT,即期望利潤(rùn)等于目標(biāo)成本的5%。 2) 當(dāng)區(qū)間(CFL,CFU)的中點(diǎn)小于目標(biāo)成本CT時(shí),E(PF)>0.05CT,即期望利潤(rùn)要高于目標(biāo)成本的5%。 3) 當(dāng)區(qū)間(CFL,CFU)的中點(diǎn)大于目標(biāo)成本CT時(shí),E(PF)<0.05CT,即期望利潤(rùn)要低于目標(biāo)成本的5%。 當(dāng)然,對(duì)于條件{CFL 通過(guò)觀察式(18)發(fā)現(xiàn),當(dāng)區(qū)間(CFL,CFU)的中點(diǎn)小于目標(biāo)成本CT時(shí),隨著成本分?jǐn)偙壤鼳的增大,E(PF)不斷增加,但當(dāng)A增大到一定程度A0時(shí),期望利潤(rùn)達(dá)到一個(gè)最大值E(PF)max,此時(shí)再增大A,期望利潤(rùn)將不再增大,稱(chēng)E(PF)max為最大期望利潤(rùn)。 當(dāng)A足夠大時(shí),根據(jù)式(8),α將變得很小,區(qū)間[(1-α)CT, (1+α)CT]將不斷縮小,一旦滿足CFL< (1-α)CT, (1+α)CT 圖3 定價(jià)模式2下承包商的最大期望利潤(rùn)Fig.3 Maximum expected profit for contractor under Cost strategy 2 剛才證明了存在最大期望利潤(rùn),下面利用公式推導(dǎo)方式證明存在E(PF)max,并給出其取值。 根據(jù)式(17),當(dāng)滿足CFL< (1-α)CT, (1+α)CT (19) 式中: 代入式(19),可算得 (20) 即最大期望利潤(rùn)可由式(20)算出。顯然,由于CT>CFL,最大期望利潤(rùn)為正值。 A0對(duì)應(yīng)于區(qū)間(CFL,CFU)剛好完全覆蓋區(qū)間[(1-α)CT, (1+α)CT]的情形,則有 (21) 式中:α1對(duì)應(yīng)于CFL剛好與圖3中D點(diǎn)重合時(shí)的α值;α2對(duì)應(yīng)于CFU剛好與圖3中H點(diǎn)重合時(shí)的α值,顯然,應(yīng)選擇α1和α2中較小者α0方能使得區(qū)間(CFL,CFU)完全覆蓋DH。 將式(8)代入式(21),可算得 2.1.3 定價(jià)模式3 將式(11)代入式(14): (23) 這意味著固定利潤(rùn)率法的期望利潤(rùn)始終等于成本區(qū)間(CFL,CFU)均值的5%。 2.2.1 定價(jià)模式1 與期望利潤(rùn)的計(jì)算類(lèi)似,期望價(jià)格等于實(shí)際成本為CFi時(shí)的價(jià)格VFi與實(shí)際成本為CFi的概率的累積求和: 式中:N和P(CFi)的含義同式(12)。 根據(jù)式(6),上式可變形為 (24) 式中:E(PF)表示期望利潤(rùn),可由式(14)~式(16) 算得。 當(dāng)CFL (25) 可以看出,當(dāng)x=0時(shí),期望價(jià)格等于(CFU+CFL)/2+PT,即軍方承擔(dān)全部風(fēng)險(xiǎn)時(shí),此時(shí)軍方的期望價(jià)格等于軍方預(yù)估的成本均值與目標(biāo)利潤(rùn)之和。 2.2.2 定價(jià)模式2 與定價(jià)模式1類(lèi)似,根據(jù)式(9)和式(10), (26) 式中:E(PF)表示期望利潤(rùn),可由式(17)~式(18)算得。 當(dāng)CFL 0.05CT (27) 可以看出,當(dāng)A=1時(shí),期望價(jià)格等于CT+0.05CT,即承包商承擔(dān)全部風(fēng)險(xiǎn)時(shí),此時(shí)軍方的期望價(jià)格等于目標(biāo)成本和5%的利潤(rùn),剛好和固定利潤(rùn)率法一致;當(dāng)A=0時(shí),期望價(jià)格等于(CFU+CFL)/2+0.05CT,即軍方承擔(dān)全部風(fēng)險(xiǎn)時(shí),此時(shí)軍方的期望價(jià)格等于軍方預(yù)估的成本均值與目標(biāo)成本的5%利潤(rùn)之和。 從式(24)和式(26)可以看出,期望價(jià)格始終等于期望利潤(rùn)與軍方預(yù)估的成本均值之和,因此分析過(guò)程和期望利潤(rùn)完全是類(lèi)似的。 根據(jù)式(26),可得最大期望價(jià)格: (28) 2.2.3 定價(jià)模式3 對(duì)于固定利潤(rùn)法,價(jià)格等于1.05CF,則有 (29) 這意味著固定利潤(rùn)率法的期望價(jià)格為定值,由成本區(qū)間(CFL,CFU)均值決定。 本節(jié)結(jié)合幾個(gè)實(shí)例,比較以上幾種定價(jià)模式,并分析如何通過(guò)承包商的期望利潤(rùn)和軍方的期望價(jià)格,來(lái)實(shí)現(xiàn)激勵(lì)約束定價(jià)機(jī)制設(shè)計(jì)。 例1 某項(xiàng)目的目標(biāo)成本為1 000萬(wàn)元,在論證階段給出了其成本上限為1 300萬(wàn)元,成本下限為800萬(wàn)元,假設(shè)目標(biāo)利潤(rùn)為50萬(wàn)元(取目標(biāo)成本的5%),對(duì)于定價(jià)模式1的最低利潤(rùn)不小于10萬(wàn)元,比較不同定價(jià)模式下相同成本分?jǐn)偙壤龑?duì)應(yīng)的實(shí)際利潤(rùn)(為便于分析,假設(shè)不同定價(jià)模式下的分?jǐn)偙壤嗤矗簒=y=A)。 表2中給出了幾種定價(jià)模式下,不同成本分?jǐn)偙壤碌睦麧?rùn)與實(shí)際成本。圖4給出了利潤(rùn)隨實(shí)際成本的變化情況。 表2 不同成本分?jǐn)偙壤碌睦麧?rùn)比較Table 2 Comparisons of profit under different cost allocation rates 萬(wàn)元 圖4 利潤(rùn)隨實(shí)際成本的變化情況Fig.4 Variation of profits with actual cost 1) 相同分?jǐn)偙壤闆r下,定價(jià)模式1對(duì)于承包商節(jié)約成本的激勵(lì)作用更好。當(dāng)實(shí)際成本等于1 200 萬(wàn)元時(shí),定價(jià)模式2的利潤(rùn)在成本分?jǐn)偙壤秊?.3,0.5,0.7的情況下將為0,可見(jiàn),成本超過(guò)上限將得不到任何利潤(rùn),這可能帶來(lái)虛報(bào)成本,比如虛報(bào)1 300萬(wàn)元,則可得利潤(rùn)為1 300-1 200=100 萬(wàn)元;而定價(jià)模式1此時(shí)還能拿到高出利潤(rùn)下限(10 萬(wàn)元)的利潤(rùn)23.33 萬(wàn)元。 2) 相同分?jǐn)偙壤闆r下,對(duì)于定價(jià)模式1,承包商在成本低于成本下限800 萬(wàn)元時(shí),沒(méi)有動(dòng)力再進(jìn)一步降低成本。當(dāng)成本達(dá)到成本下限時(shí),再降低成本時(shí)利潤(rùn)將始終保持在利潤(rùn)上限,這意味著不鼓勵(lì)將成本降低到最低成本以下,比如圖4(b) 中,成本為800 萬(wàn)元時(shí),利潤(rùn)是110 萬(wàn)元,成本再降低到700 萬(wàn)元,利潤(rùn)還是110 萬(wàn)元。 3) 相同分?jǐn)偙壤闆r下,對(duì)于定價(jià)模式1,保證了成本超出范圍時(shí),不至于利潤(rùn)過(guò)高或過(guò)低。圖4給出了利潤(rùn)隨實(shí)際成本的變化情況。假設(shè)分?jǐn)偙壤鶠?0%,如圖4(a)所示,可以看出,定價(jià)模式1和定價(jià)模式2的實(shí)際利潤(rùn)在成本上下限范圍內(nèi)完全相同,但是超出上限部分,定價(jià)模式2的實(shí)際利潤(rùn)要高于模式1,低于下限部分,實(shí)際利潤(rùn)要低于模式1,這是因?yàn)槎▋r(jià)模式1根據(jù)成本分?jǐn)偙壤墒?3)和式(4)反算出了最低利潤(rùn)和最高利潤(rùn)值,保證成本超出范圍時(shí),不至于利潤(rùn)過(guò)高或過(guò)低。 4) 相同分?jǐn)偙壤闆r下,定價(jià)模式1保證了成本超過(guò)上限時(shí)能夠得到最低利潤(rùn)。假設(shè)設(shè)定分?jǐn)偙壤鶠?0%,結(jié)果如圖4(b)所示,可以看出,定價(jià)模式1的實(shí)際利潤(rùn)要始終優(yōu)于定價(jià)模式2。假設(shè)超支的分?jǐn)偙壤秊?0%,則根據(jù)式(1),最低利潤(rùn)將為-40萬(wàn)元,故可將最低利潤(rùn)PD設(shè)定為10萬(wàn)元,然后利用式(3)反算出x=0.133 3,即實(shí)際的超支分?jǐn)偙壤陀?0%。 5) 定價(jià)模式3的實(shí)際利潤(rùn)是成本越大越好,如圖4所示,在成本節(jié)約時(shí),利潤(rùn)少于前2種定價(jià)模式,在成本超支時(shí),利潤(rùn)超過(guò)前2種定價(jià)模式。 例2 已知條件同例1,為承包商設(shè)計(jì)合理的激勵(lì)約束定價(jià)策略(即設(shè)計(jì)成本分?jǐn)偙壤?,使得其期望利潤(rùn)不低于80 萬(wàn)元。 已知承包商預(yù)估項(xiàng)目的成本范圍(CFL,CFU)分別取(700,1 100)萬(wàn)元, (900,1 100)萬(wàn)元, (900,1 200)萬(wàn)元, (800,1 300)萬(wàn)元時(shí),令成本分?jǐn)偙壤謩e為0.3, 0.5, 0.7的情況下,期望利潤(rùn)如表3所示。圖5給出了分別取分?jǐn)偙壤秊?.1~0.9之間變化時(shí),期望利潤(rùn)的變化曲線。根據(jù)式(23),定價(jià)模式3(固定利潤(rùn)率法)的期望利潤(rùn)始終等于成本區(qū)間(CFL,CFU)均值的5%。 1) 當(dāng)(CFL,CFU)= (700,1 100)萬(wàn)元時(shí),此時(shí)區(qū)間(CFL,CFU)的中點(diǎn)小于目標(biāo)成本1 000 萬(wàn)元,如表3和圖5(a)所示,顯然,對(duì)于定價(jià)模式1,分?jǐn)偙壤酱髣t期望利潤(rùn)越高,當(dāng)取分?jǐn)偙壤坏陀?2%時(shí),能夠達(dá)到期望利潤(rùn)不低于80 萬(wàn)元的要求;對(duì)于定價(jià)模式2,分?jǐn)偙壤酱髣t期望利潤(rùn)越高,但是當(dāng)分?jǐn)偙壤^(guò)50%時(shí),期望利潤(rùn)最大為75萬(wàn)元,因此,無(wú)法滿足承包商的期望利潤(rùn)值。 2) 當(dāng)(CFL,CFU)= (900,1 100)萬(wàn)元時(shí),此時(shí)區(qū)間(CFL,CFU)的中點(diǎn)剛好等于目標(biāo)成本1 000 萬(wàn)元,如表3和圖5(b)所示,對(duì)于定價(jià)模式1,分?jǐn)偙壤酱髣t期望利潤(rùn)越高,但是期望利潤(rùn)始終達(dá)不到80萬(wàn)元;而對(duì)于定價(jià)模式2,期望利潤(rùn)始終為50萬(wàn)元,這是因?yàn)槟繕?biāo)成本CT位于區(qū)間(CFL,CFU)的中點(diǎn),根據(jù)式(18)可得出此結(jié)論。 3) 當(dāng)(CFL,CFU)= (900,1 200)萬(wàn)元時(shí),此時(shí)區(qū)間(CFL,CFU)的中點(diǎn)大于目標(biāo)成本1 000 萬(wàn)元,如表3 和圖5(c)所示,對(duì)于定價(jià)模式1,分?jǐn)偙壤酱髣t期望利潤(rùn)出現(xiàn)了先減后增,但是期望利潤(rùn)不超過(guò)56.111 萬(wàn)元,始終達(dá)不到80 萬(wàn)元;而對(duì)于定價(jià)模式2,分?jǐn)偙壤酱髣t期望利潤(rùn)越低,根據(jù)式(18),期望利潤(rùn)將始終低于目標(biāo)成本的5%,即少于50 萬(wàn)元,無(wú)法滿足承包商的期望利潤(rùn)值。 4) 當(dāng)(CFL,CFU)= (800,1 300)萬(wàn)元時(shí),此時(shí)區(qū)間(CFL,CFU)的中點(diǎn)與情形3)相同,大于目標(biāo)成本1 000 萬(wàn)元,如表3和圖5(d)所示,對(duì)于定價(jià)模式1,期望利潤(rùn)不超過(guò)74 萬(wàn)元,達(dá)不到80 萬(wàn)元;對(duì)于定價(jià)模式2,分?jǐn)偙壤酱髣t期望利潤(rùn)越低,根據(jù)式(18),期望利潤(rùn)也將始終低于50 萬(wàn)元,無(wú)法滿足承包商的期望利潤(rùn)值。 5) 通過(guò)與固定利潤(rùn)率法對(duì)比,當(dāng)承包商預(yù)估的成本均值低于目標(biāo)成本時(shí),2種定價(jià)模式的期望利潤(rùn)都高于固定利潤(rùn)率法;當(dāng)均值等于目標(biāo)成本時(shí),定價(jià)模式1的期望利潤(rùn)最大;當(dāng)均值高于目標(biāo)成本時(shí),定價(jià)模式1的期望利潤(rùn)不低于定價(jià)模式2,但有可能低于固定利潤(rùn)率法。 綜上分析,可得出以下結(jié)論:在定價(jià)模式1下,承包商應(yīng)盡量追求成本分?jǐn)偙壤酱笤胶茫珣?yīng)注意當(dāng)承包商預(yù)估的成本范圍均值大于目標(biāo)成本時(shí),期望利潤(rùn)會(huì)出現(xiàn)一個(gè)先減后增的趨勢(shì),應(yīng)結(jié)合圖5(c),選取合適的成本分?jǐn)偙壤T诙▋r(jià)模式2情況下,承包商的期望利潤(rùn)具體越大越好還是越少越好,與承包商預(yù)估的成本范圍均值有關(guān),如果均值是節(jié)約的,則分?jǐn)偙壤酱笤胶茫嬖谝粋€(gè)最大值點(diǎn)A0,達(dá)到A0后再增大比例對(duì)于期望利潤(rùn)沒(méi)有影響,如果均值是超支的,則分?jǐn)偙壤叫≡胶茫瑯哟嬖谝粋€(gè)最大值點(diǎn)A0,達(dá)到A0后再增大比例對(duì)于期望利潤(rùn)沒(méi)有影響。 表3 不同定價(jià)模式下的期望利潤(rùn)對(duì)比Table 3 Comparison of expected profits under different cost strategies 萬(wàn)元 圖5 期望利潤(rùn)隨分?jǐn)偙壤淖兓闆rFig.5 Variation of expected profits with cost allocation rates 例3 已知條件同例1,為軍方設(shè)計(jì)合理的激勵(lì)約束定價(jià)策略(即設(shè)計(jì)成本分?jǐn)偙壤?,使得其期望價(jià)格不高于1 000 萬(wàn)元。 表4中給出了幾種定價(jià)模式下,已知軍方預(yù)估項(xiàng)目的成本范圍(CFL,CFU)分別取(700,1 100)萬(wàn)元, (900,1 100)萬(wàn)元, (900,1 200)萬(wàn)元, (800,1 300)萬(wàn)元時(shí),令成本分?jǐn)偙壤謩e為0.3, 0.5, 0.7時(shí)的期望價(jià)格。圖6給出了分別取分?jǐn)偙壤秊?.1~0.9之間變化時(shí),期望價(jià)格的變化曲線。 分析過(guò)程與例2類(lèi)似,可得出以下結(jié)論: 1) 在定價(jià)模式1情況下,軍方應(yīng)盡量追求成本分?jǐn)偙壤叫≡胶?注意,這里的分?jǐn)偙壤y(tǒng)一指的是承包商的成本分?jǐn)偙壤?,如圖6(a)和圖6(b)所示,但應(yīng)注意當(dāng)軍方預(yù)估的成本范圍均值大于目標(biāo)成本時(shí),期望價(jià)格會(huì)出現(xiàn)一個(gè)先減后增的趨勢(shì),這說(shuō)明存在一個(gè)使得期望價(jià)格最小的分?jǐn)偙壤鐖D6(c)和圖6(d)所示,可作為軍方的最佳成本分?jǐn)偙壤?/p> 2) 在定價(jià)模式2情況下,軍方的期望價(jià)格與軍方預(yù)估的成本范圍均值有關(guān),如果均值低于目標(biāo)成本,則分?jǐn)偙壤叫≡胶茫鐖D6(a)所示;如果均值是剛好等于目標(biāo)成本,則期望價(jià)格將保持不變,即與分?jǐn)偙壤裏o(wú)關(guān),如圖6(b)所示;如果均值高于目標(biāo)成本,則分?jǐn)偙壤酱笤胶茫瑯哟嬖谝粋€(gè)最大值點(diǎn)A0,達(dá)到A0后再增大比例對(duì)于期望價(jià)格沒(méi)有影響,如圖6(c)和圖6(d)所示。 表4 不同定價(jià)模式下的期望價(jià)格對(duì)比Table 4 Comparisons of expected prices under different cost strategies 萬(wàn)元 圖6 期望價(jià)格隨分?jǐn)偙壤淖兓闆rFig.6 Variation of expected prices with cost allocation rates 例4 已知條件同例1,假設(shè)承包商期望利潤(rùn)不低于80 萬(wàn)元,承包商預(yù)估項(xiàng)目的成本范圍為(700,1 100)萬(wàn)元,軍方的期望價(jià)格不高于1 000 萬(wàn)元,軍方的預(yù)估項(xiàng)目的成本范圍為(700,1 100)萬(wàn)元,試設(shè)計(jì)雙方滿意的激勵(lì)約束定價(jià)策略(即設(shè)計(jì)成本分?jǐn)偙壤?。 對(duì)于定價(jià)模式1,根據(jù)表3和表4,承包商滿意的分?jǐn)偙壤秊椋簒≤13.3%,y>32%,期望利潤(rùn)>80.333萬(wàn)元;軍方滿意的分?jǐn)偙壤秊椋簒≥13.3%,y<52%,期望價(jià)格<1 000.3 萬(wàn)元。因此,可設(shè)計(jì)超支的成本分?jǐn)偙壤秊?3.3%,節(jié)約的成本分?jǐn)偙壤幱?32%, 52%)之間,即可達(dá)到雙方都滿意的定價(jià)方案。比如,當(dāng)x=13.3%,y=40%時(shí),根據(jù)式(3)和式(4),可算得利潤(rùn)上下限分別為10.1 萬(wàn)元和130 萬(wàn)元,軍方期望價(jià)格為988.34 萬(wàn)元,承包商的期望利潤(rùn)為88.337 萬(wàn)元,均滿足要求。 對(duì)于定價(jià)模式2,根據(jù)表3和表4,無(wú)論分?jǐn)偙壤绾危邪痰钠谕麧?rùn)最大只有75 萬(wàn)元,而軍方始終可以得到滿意的期望價(jià)格,此時(shí),承包商應(yīng)適當(dāng)調(diào)低其期望利潤(rùn)值,方能得到滿意的激勵(lì)約束定價(jià)方案。 從例4可以看出,相同條件下,對(duì)于定價(jià)模式1,承包商可以得到更多的期望利潤(rùn),軍方和承包商更容易達(dá)成一致的成本分?jǐn)偙壤?/p> 通過(guò)比較3種不同的定價(jià)模式,即2種激勵(lì)約束定價(jià)模式和傳統(tǒng)的固定利潤(rùn)率定價(jià)模式,得出以下建議: 1) 通過(guò)例1可以看出,定價(jià)模式1在激勵(lì)約束效果上優(yōu)于模式2。從承包商角度來(lái)看,一方面,定價(jià)模式1和2在成本達(dá)到各自成本上限時(shí),都將只能得到最低利潤(rùn),即定價(jià)模式2的利潤(rùn)將為0,而定價(jià)模式1保底能夠拿到最低利潤(rùn)(即利潤(rùn)下限,高于定價(jià)模式2);另一方面,一般地,在相同的分?jǐn)偙壤拢▋r(jià)模式1的成本上限要高于定價(jià)模式2,這意味著隨著成本的增加,定價(jià)模式2將更快降低到0利潤(rùn),而定價(jià)模式1將較慢地降低到保底利潤(rùn),例如,從表2可以看出,在相同的分?jǐn)偙壤?假設(shè)為0.7),定價(jià)模式2在成本為1 100 萬(wàn)元時(shí)已經(jīng)達(dá)到成本上限,而定價(jià)模式1在成本為1 100 萬(wàn)元時(shí)仍有36.67 萬(wàn)元的利潤(rùn)(尚未降低到利潤(rùn)下限)。綜合以上分析,相比定價(jià)模式2,定價(jià)模式1對(duì)于承包商在成本超支時(shí)的保護(hù)作用更強(qiáng),承包商因“無(wú)利可圖”而虛報(bào)成本的可能性將更低。 2) 定價(jià)模式2主要采取承包商承擔(dān)70%的激勵(lì)約束成本的模式(即A=0.7)[15],從表3可以看出,無(wú)論承包商的預(yù)估成本范圍如何,承包商的最大期望利潤(rùn)都將低于定價(jià)模式1,且期望利潤(rùn)隨著分?jǐn)偙壤淖兓容^小,導(dǎo)致分?jǐn)偙壤鳛檎{(diào)控利潤(rùn)參數(shù)的作用弱化。 3) 給出判斷激勵(lì)約束定價(jià)機(jī)制好壞的標(biāo)準(zhǔn)。 一是應(yīng)能夠激勵(lì)承包商不斷降低成本,成本越低越好,即使得承包商成本控制得越低,得到利潤(rùn)回報(bào)越高,顯然,定價(jià)模式3(固定利潤(rùn)率法)是不合適的。 二是考慮到裝備研制項(xiàng)目的風(fēng)險(xiǎn)性,承包商應(yīng)能在成本超支時(shí)得到一定利潤(rùn)(少于成本節(jié)約時(shí)的利潤(rùn)),而不是利潤(rùn)為0,這方面定價(jià)模式1要優(yōu)于定價(jià)模式2。 三是承包商的風(fēng)險(xiǎn)分?jǐn)偙壤礁撸瑒t成本節(jié)約時(shí)利潤(rùn)越大,成本超支時(shí)利潤(rùn)越小,這方面2種定價(jià)模式都可滿足。 四是風(fēng)險(xiǎn)分?jǐn)偙壤鳛檎{(diào)控激勵(lì)約束定價(jià)機(jī)制的主要指標(biāo),應(yīng)對(duì)承包商的期望利潤(rùn)具有較大的調(diào)控區(qū)間,從圖5可以看出,顯然定價(jià)模式2在分?jǐn)偙壤_(dá)到一定值時(shí),將不再改變,而定價(jià)模式1則始終能夠調(diào)控期望利潤(rùn)。 綜上分析,定價(jià)模式1要優(yōu)于定價(jià)模式2,但模式2保留了傳統(tǒng)5%目標(biāo)利潤(rùn)的特點(diǎn),是固定利潤(rùn)法的一種過(guò)渡。這里根據(jù)以上分析,參考2種定價(jià)模式的特點(diǎn),設(shè)計(jì)一種新的定價(jià)策略,如圖7所示,其實(shí)施步驟如下: 步驟1 在論證階段確定目標(biāo)成本估算值,包括:目標(biāo)成本CT,成本上限CU,成本下限CD,比如利用PRICE軟件在進(jìn)行目標(biāo)成本估算時(shí),通過(guò)進(jìn)行不確定性分析,確定了置信度50%的成本點(diǎn)為目標(biāo)成本,置信度75%的成本點(diǎn)為上限成本。 步驟2 以目標(biāo)成本的5%作為目標(biāo)利潤(rùn),這和定價(jià)模式2是類(lèi)似的,作為固定利潤(rùn)法的一種過(guò)渡,當(dāng)然,目標(biāo)利潤(rùn)值也可適當(dāng)調(diào)整,建議取值在5%~10%之間。 步驟3 承包商和軍方共同協(xié)商確定最低利潤(rùn)值PFmin,注意PFmin應(yīng)大于0,同時(shí)PFmin與利潤(rùn)下限PD不同:當(dāng)x已知時(shí),利用式(3)可算出PD,若此時(shí)PD≤PFmin,則令PD=PFmin,并代入式(3) 反算出x,作為實(shí)際的成本超支分?jǐn)偙壤H鬚D>PFmin,則PD仍為利潤(rùn)下限值。 步驟4 承包商擬定期望利潤(rùn),軍方制定期望價(jià)格,同時(shí),承包商根據(jù)期望利潤(rùn)值要求,以及承包商預(yù)估的成本范圍,按照2.1節(jié)方法確定對(duì)承包商有利的分?jǐn)偙壤?x和y),軍方根據(jù)期望價(jià)格要求,以及軍方預(yù)估的成本范圍,按照2.2節(jié)方法確定對(duì)軍方有利的分?jǐn)偙壤?x和y)。 步驟5 如果軍方和承包商對(duì)于分?jǐn)偙壤軌蜻_(dá)成一致,則確定最終分?jǐn)偙壤鶕?jù)式(3)和式(4)算出利潤(rùn)上下限,根據(jù)實(shí)際成本,按照式(5)和式(6)計(jì)算實(shí)際利潤(rùn)和價(jià)格;否則,承包商和軍方適當(dāng)調(diào)整各自的期望利潤(rùn)和期望價(jià)格,返回步驟4。 例5 假設(shè)論證階段確定目標(biāo)成本估算值,目標(biāo)成本為1 000 萬(wàn)元,成本上限為1 300 萬(wàn)元,下限為800 萬(wàn)元。根據(jù)步驟 2,以目標(biāo)成本的5%作為目標(biāo)利潤(rùn),即目標(biāo)利潤(rùn)設(shè)為50 萬(wàn)元。假設(shè)承包商和軍方共同協(xié)商確定最低利潤(rùn)值PFmin=14 萬(wàn)元(利用式(3)反算出當(dāng)PD取PFmin時(shí),x=0.12)。 1) 假設(shè)承包商的期望利潤(rùn)為不低于80 萬(wàn)元,軍方的期望價(jià)格為不高于1 000 萬(wàn)元,承包商預(yù)估的成本范圍為:(700,1 100)萬(wàn)元,軍方的預(yù)估項(xiàng)目的成本范圍為(700,1 100)萬(wàn)元。 按照2.1節(jié)方法算出對(duì)承包商有利的分?jǐn)偙壤簒≤0.12,y≥0.32(如圖8(a)所示),按照2.2節(jié) 方法算出對(duì)軍方有利的分?jǐn)偙壤簒≥0.12,y≤0.51(如圖8(b)所示)。因此,可設(shè)計(jì)超支的成本分?jǐn)偙壤秊?.12,節(jié)約的成本分?jǐn)偙壤幱赱0.32, 0.51]之間。不妨假設(shè),經(jīng)過(guò)協(xié)商,雙方確定分?jǐn)偙壤秊椋簒=0.12,y=0.4,根據(jù)式(3)和式(4) 可算出利潤(rùn)上下限:PD=14 萬(wàn)元,PU=130 萬(wàn)元。 圖7 裝備激勵(lì)約束定價(jià)策略實(shí)施步驟Fig.7 Procedure of incentive constraints pricing strategy for equipment 圖8 滿足承包商和軍方期望價(jià)格的分?jǐn)偙壤鼺ig.8 Cost allocation rates that satisfy contractors’ expected profit and military’s expected price 假設(shè)實(shí)際成本CF=900 萬(wàn)元,由式(5)和式(6) 可算出實(shí)際利潤(rùn)和價(jià)格:PF=90 萬(wàn)元,VF=990 萬(wàn)元。 2) 其他條件不變,假設(shè)軍方的期望價(jià)格為不高于970 萬(wàn)元。類(lèi)似地,按照2.1節(jié)方法算出對(duì)承包商有利的分?jǐn)偙壤簒≤0.12,y≥0.32(如圖8(a) 所示),按照2.2節(jié)方法算出對(duì)軍方有利的分?jǐn)偙壤簒≥0.12,y≤0.21(可從圖8(b)中看出)。顯然,雙方不可能達(dá)成一致,需要由承包商和軍方適當(dāng)調(diào)整各自的期望利潤(rùn)和期望價(jià)格。 當(dāng)前裝備定價(jià)模式改革的重點(diǎn)之一,就是要改變傳統(tǒng)的固定利潤(rùn)率定價(jià)模式,這種定價(jià)模式不但不鼓勵(lì)承包商主動(dòng)降低成本,而是鼓勵(lì)承包商提高成本,成本越高,利潤(rùn)就越高。激勵(lì)約束定價(jià)模式能夠在一定程度上激勵(lì)承包商主動(dòng)降低成本,是未來(lái)裝備定價(jià)的主要趨勢(shì)。 1) 本文對(duì)美軍和我軍的激勵(lì)約束定價(jià)模式進(jìn)行了對(duì)比分析,比較了2種定價(jià)模式的機(jī)理以及對(duì)軍方和承包商的期望價(jià)格和期望利潤(rùn)的影響。 2) 美軍激勵(lì)約束定價(jià)模式采取的是先確定利潤(rùn)下限和上限,再確定分?jǐn)偙壤哪J剑疚膭t提出根據(jù)期望利潤(rùn)和期望價(jià)格先確定分?jǐn)偙壤缓笤俅_定利潤(rùn)上下限,并據(jù)此設(shè)計(jì)了一種新的激勵(lì)約束定價(jià)策略。 3) 當(dāng)然,激勵(lì)約束定價(jià)模式成功的前提還在于對(duì)成本指標(biāo)的準(zhǔn)確估算,從本文分析可以看出,目標(biāo)成本、成本上下限值將會(huì)直接影響激勵(lì)約束定價(jià)策略,而目標(biāo)成本估算不準(zhǔn)也是制約激勵(lì)約束定價(jià)模式改革的重要因素之一,隨著現(xiàn)代成本估算手段的不斷進(jìn)步以及數(shù)據(jù)的不斷積累,相信激勵(lì)約束定價(jià)模式一定能夠在控制成本、提高承包商積極性方面發(fā)揮積極有效的作用。1.2 定價(jià)模式2
1.3 定價(jià)模式3
2 不同定價(jià)模式比較分析
2.1 承包商的期望利潤(rùn)
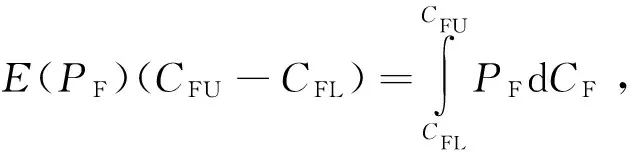

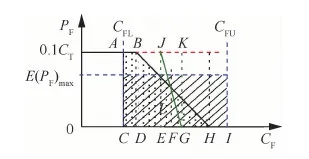
2.2 軍方的期望價(jià)格
3 實(shí)例分析
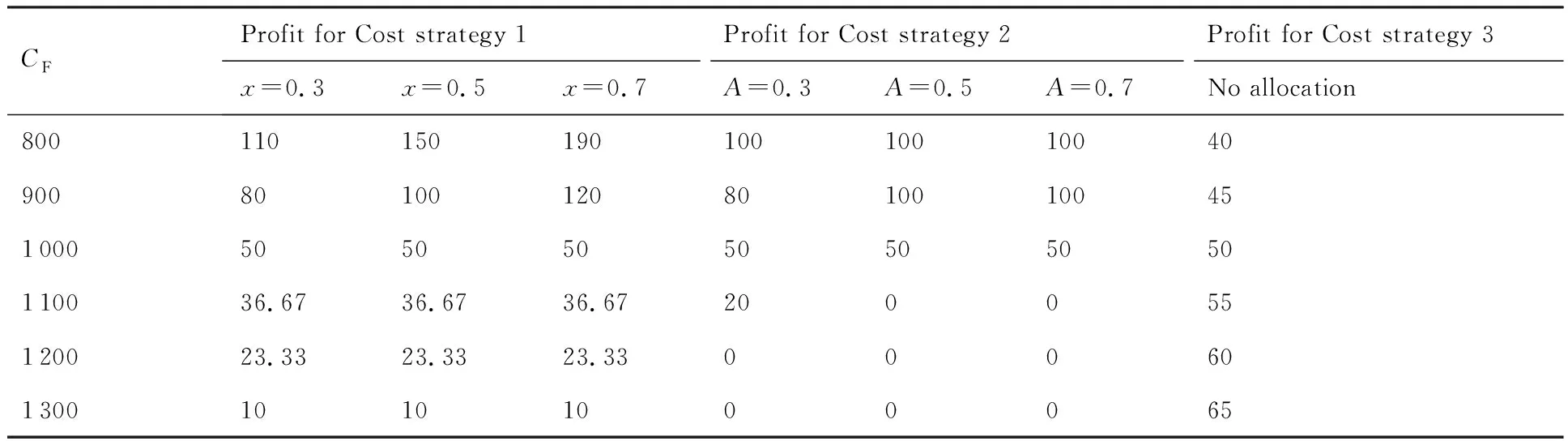
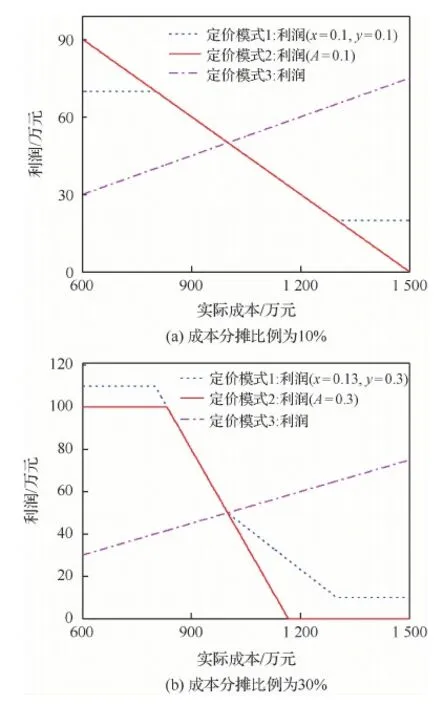
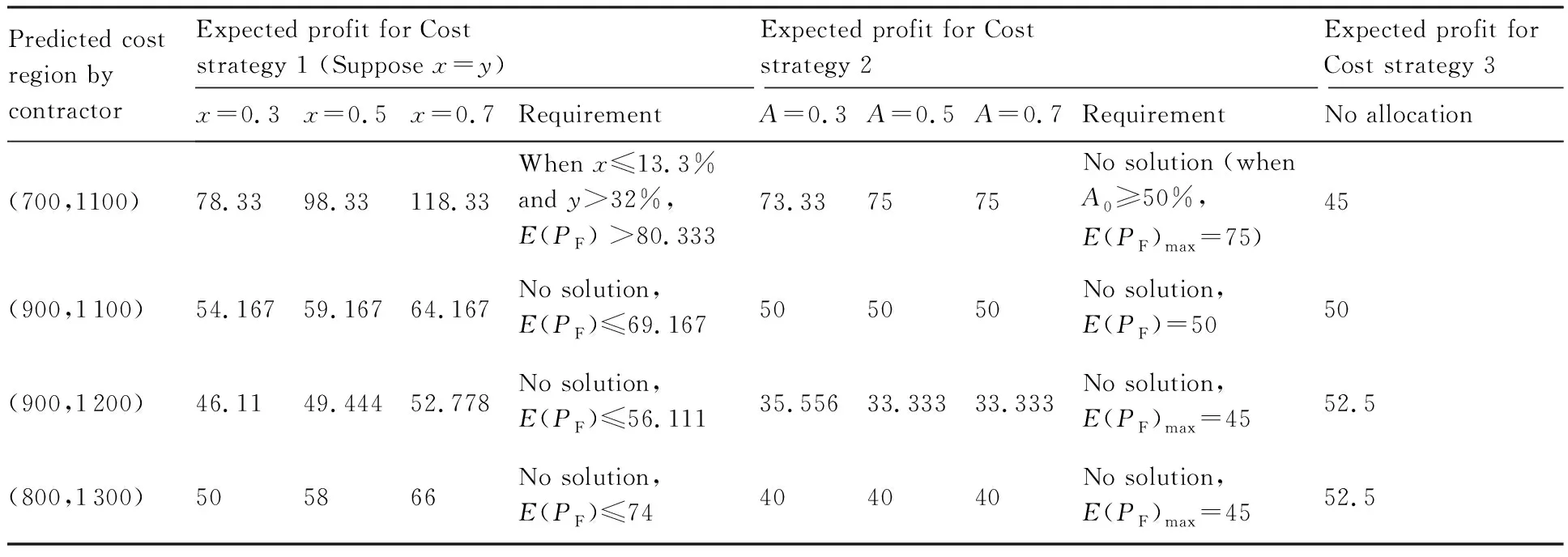

4 裝備激勵(lì)約束定價(jià)機(jī)制設(shè)計(jì)
5 結(jié) 論

