包含乘性噪聲自適應修正的非合作目標相對導航算法

朱云峰，孫永榮，趙偉，黃斌，吳玲

南京航空航天大學 自動化學院，南京 210016

近年來，隨著無人機應用領域的不斷拓展，其對態勢感知的要求也越來越高，尤其是對于未知環境的探索能力，是急需攻克的重點問題。相對導航作為其中的核心技術之一[1]，在未來的智能物流、集群作戰[2]、搜索救援和編隊飛行[3]等多種場合都至關重要。因此，實時、高精度、高可靠性的相對狀態估計算法逐漸成為研究的熱點內容[4]。

非合作目標的相對導航主要是指在沒有通信條件，或者目標上沒有配置主動傳感器的情況下的相對定位問題[5]。合適的傳感器選擇是非常關鍵的。目前，對于中遠距離的相對導航，根據傳感器的測量原理可以分為多種，包括視覺傳感器、雷達、IRST(Infrared Search and Track)和ESM(Electronic Support Measures)等以波達角度(Angle of Arrival，AOA)或距離為量測的傳感器[6]，或者以波達時間(Time of Arrival，TOA)[7]、波達頻率(Frequency of Arrival，FOA)[8]、波達時間差(Time Difference of Arrival，TDOA)[9]等為量測值的無線電設備。本文以視線仰角、視線方位角和無人機與目標之間的直線距離作為傳感器輸出來估計相對狀態。

對于非線性系統的狀態估計算法，目前擴展卡爾曼濾波(EKF)算法是使用最廣的，但由于其經過泰勒展開后取一階線性近似[10-11]，忽略了高階項的非線性特性，在一些強非線性的情況下導致濾波精度嚴重下降，并且收斂速度緩慢[12]。為了進一步改善算法的性能，迭代擴展卡爾曼濾波(IEKF)算法發展起來，并開始得到應用。但該算法通過多次使用量測值實現，當迭代初值或者協方差誤差較大時，容易找不到極值點，明顯降低了濾波器的精度[13]。同時，對于非合作目標相對導航系統而言，距離的測量往往與信號特性相關聯，測量中的抖動振動造成安裝矩陣與基準之間的偏轉以及信號能量的衰減都會引入乘性誤差[14-15]。但目前的相對導航濾波算法基本都將距離量測噪聲設定為加性噪聲，沒有對因相對距離的增加而引入的乘性量測噪聲進行修正，如果只是簡單地以傳感器的標稱值或實驗室測定值設置濾波中的噪聲陣，必將導致濾波精度的污染[16]，造成仿真實驗和實際的不一致性。

鑒于上述的問題，本文通過分析IEKF算法中的迭代過程，利用LM(Levenberg-Marguardt)優化的思想進行改進，提出了一種LM-IEKF(Levenberg-Marquardt Iterative Extended Kalman Filter)算法，考慮到乘性噪聲情況下的精度下降問題，又進一步提出了包含有量測噪聲自適應修正的Modified LM-IEKF算法。最后，通過對比分析驗證了本文算法的有效性。

1 非合作目標相對導航系統模型

非合作目標的相對導航是通過無人機對目標進行測角測距來實現的，無人機與目標之間的位置關系如圖1所示，xyz坐標系為地心空間直角坐標系，ρ為無人機測得的目標距離,β和α分別為無人機對目標探測得到的視線仰角和視線方位角(本文中規定視線方位角為與x軸正方向的夾角)。

圖1 相對導航原理示意圖Fig.1 Schematic diagram of relative navigation

根據定位原理，可以得到空間幾何模型。將無人機的絕對位置坐標記為Xu=[xu,yu,zu]T，目標的絕對位置坐標記為Xt=[xt,yt,zt]T。相對導航的目的就是利用無人機上配置的傳感器測量得到距離和角度信息[ρ,α,β]，計算出目標與無人機間的相對位置ΔX=Xt-Xu=[Δx,Δy,Δz]T。由圖2可以得到無人機與目標之間的空間幾何關系為

(1)

定義狀態變量為x= [ΔX, ΔX′, ΔX″]T，其中ΔX′和ΔX″分別為無人機與目標之間的相對速度和相對加速度。由式(1)可以建立相對導航系統的量測方程為

(2)

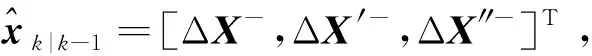
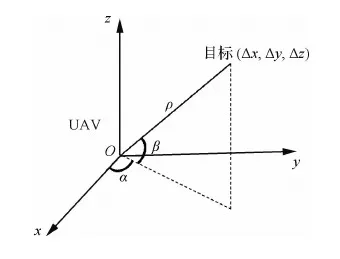
圖2 相對導航幾何空間模型示意圖Fig.2 Relative navigation geometric space model

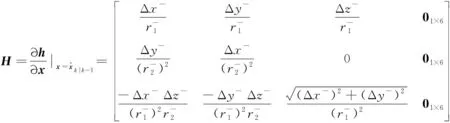
(3)

式中：

選擇勻加速(CA)模型作為相對運動模型，離散化狀態方程可表示為

xk=Φk|k-1xk-1+Γk-1wk-1

(4)

式中：狀態轉移矩陣Φk|k-1和噪聲輸入矩陣Γk-1分別為

(5)

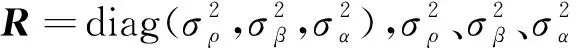
2 基于Levenberg-Marquardt優化的迭代卡爾曼濾波算法

基于上述的相對導航數學模型，本節分析了IEKF算法原理，并引入Levenberg-Marquardt優化的思想對其進行改進，進而提出了一種提高濾波穩定性的LM-IEKF算法。

2.1 現有的IEKF算法

傳統的EKF算法可以一定程度地解決非線性濾波問題，但由于其在使用泰勒階數展開時，舍去了高階項，所以濾波過程中產生了截斷誤差。尤其當系統模型存在較大的誤差時，經非線性函數放大之后可能會導致濾波結果偏差很明顯并出現濾波不穩定的情況，在實際情況中甚至會出現濾波發散。

IEKF算法是EKF的一種改進，其以狀態估計值為依據，針對觀測矩陣的計算，通過設置迭代次數進行多次更新，反復使用觀測數據，可以有效地改善狀態估計的精度[10,12,13]。

算法在k時刻的第次迭代流程如下：

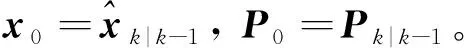
2) 求雅克比矩陣Hk,i：

(6)

3) 求增益陣Kk,i：

Kk,i=Pk|k-1(Hk,i)T(Hk,iPk|k-1(Hk,i)T+Rk)-1

(7)

(8)

5) 協方差陣遞推Pk|k,i+1：

Pk|k,i+1=(I9-Kk,iHk,i)TPk|k-1

(9)

由上述步驟可以看出，當迭代次數為1的時候，IEKF和EKF是等價的。

2.2 LM-IEKF算法

利用數學方法可以證明IEKF在本質上是和高斯牛頓迭代法等價的[17]，可以看作是高斯牛頓迭代在最大似然估計意義上的近似解。考慮到高斯牛頓在非線性迭代中的表現特點，IEKF在過程噪聲或測量噪聲過大、運動模型不準確、較大的初始誤差等多種情況下，容易出現不穩定[10,18]。據此，本文借鑒了LM方法優化高斯牛頓迭代的思想，對IEKF進行改進，以提高算法的穩定性，實現全局的最優估計。

2.2.1 狀態更新方程的推導

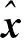
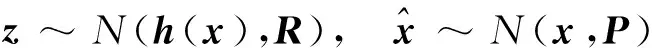
(10)

為了簡便，將當前時刻的觀測量和狀態估計值組成一個增廣的觀測向量，同理觀測矩陣也對應的進行改寫：

Z=[z,x0]T，g(x)=[h(x),x]T

(11)

由式(10)可得

(12)

對于高斯牛頓法來說，迭代公式表示為

xi+1=xi-(r′(xi)Tr′(xi))-1r′(xi)Tr(xi)

(13)

基于LM優化的思想[19-20]，將式(13)改進為

xi+1=xi-(r′(xi)Tr′(xi)+μI)-1r′(xi)Tr(xi)

(14)

式中：μ為阻尼因子，決定了迭代的方向和步長。

定義：r(x)=S(Z-g(x))

(15)

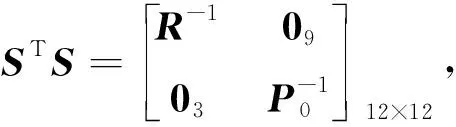
r′(x)=-Sg′(x)

(16)

其中：

(17)

將式(15)、式(16)代入式(14)中，推導出在k時刻的狀態變量第i次迭代公式為

xi+1=xi+(g′(xi)TSTSg′(xi)+μI9)-1·

g′(xi)TSTS(Z-g(xi))=xi+

(18)

根據式(17)、式(18)可以進一步推導為

(19)

2.2.2 協方差陣遞推公式的推導

根據式(12)的定義，用最大似然函數L(x)表示Z關于變量x的概率密度：

(20)

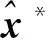
(21)

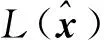
(22)

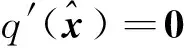
(23)

由線性化近似：

(24)

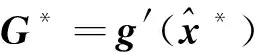
令V=Z-g(x),由式(12)可知,V～(012×1,Q)。

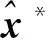
(25)

(26)

G*TQ-1E(VVT)Q-1G*(G*TQ-1G*)-1=

(G*TQ-1G*)-1

(27)

假設第k時刻，當i=n時迭代結束，由式(17) 和式(27)，可得第k時刻迭代結束后，進入到下一時刻k+1的協方差更新公式：

(28)

2.2.3 LM-IEKF算法流程推導

基于2.2.2節關于LM-IEKF算法中的狀態更新方程以及基于最大似然估計的協方差陣遞推公式的研究。本節推導了算法的整體流程。

1) 設置濾波器的初值xk0、Pk0。

(29)

3) 求一步預測的均方差陣Pk|k-1：

Pk|k-1=Φk-1Pk-1Φk-1T+Qk-1

(30)

4) 設置迭代初值：

(31)

5) 求量測陣的雅克比矩陣Hk,i：

(32)

(33)

7) 求協方差陣的遞推值Pk|k,i+1：

(34)

8) 判斷終止條件

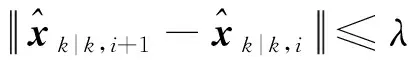
3 包含乘性噪聲自適應修正的Modified LM-IEKF算法

當實際環境中包含多種非線性的畸變、信號能量的衰減、運行過程中的抖動等情況時，都會不可避免地引入乘性噪聲。本文假設傳感器測得的距離值被污染，量測噪聲不僅包含有加性噪聲，也包含有與距離相關的乘性噪聲，并且距離的量測誤差假定與傳感器至目標之間的距離成線性關系。因此，量測矩陣可寫為

(35)

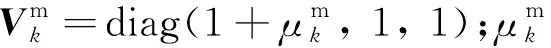
針對與距離相關的乘性噪聲，通過儲存一段時間Tm內的n個量測噪聲殘差，并計算量測噪聲統計的估計值。自適應修正方法在濾波的算法流程中，一方面對未知的噪聲統計參數進行估計，另一方面也利用量測修正狀態變量的預測值。

量測噪聲的樣本方差陣為

(36)

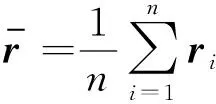
樣本方差陣的期望值為

(37)

把式(35)代入式(36)，可以得到量測噪聲協方差矩陣的估計值為

(38)

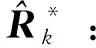
(39)

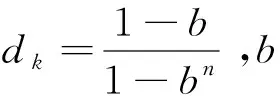
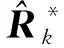
4 實驗與分析

為了驗證本文提出的LM-IEKF算法和Modified LM-IEKF算法的有效性，本文利用MATLAB采用蒙特卡羅方法，在僅含有加性噪聲和包含乘性噪聲兩種情況下展開仿真與分析，并與EKF和IEKF算法進行了比較。

4.1 仿真條件

設置仿真時間為600 s。設置傳感器的精度(3σ)為[30 m, 2 mrad, 2 mrad]，更新頻率為2 Hz。設置目標的起始位置為[118.300°， 31.0°， 8 000.0 m]，以100 m/s的速度朝北向勻速直線運動。設置無人機的起始位置為[118.30°, 31.290°, 6 250.0 m]，初始姿態角為[0°, 0°, 0°]，初始速度為[0, 100 ms, ]。無人機的軌跡參數見表1。無人機與目標的軌跡模擬由遠及近的會合過程，且無人機包含有平飛、爬升和轉彎等機動過程。本文以MAE(Mean Absolute Error)和RMSE(Root Mean Square Error)來評價算法的精度情況。圖3為以目標的起始位置為原點的相對位置示意圖。圖4為仿真設定的無人機與目標之間的相對位置和相對速度(vx,vy,vz)變化的曲線圖。

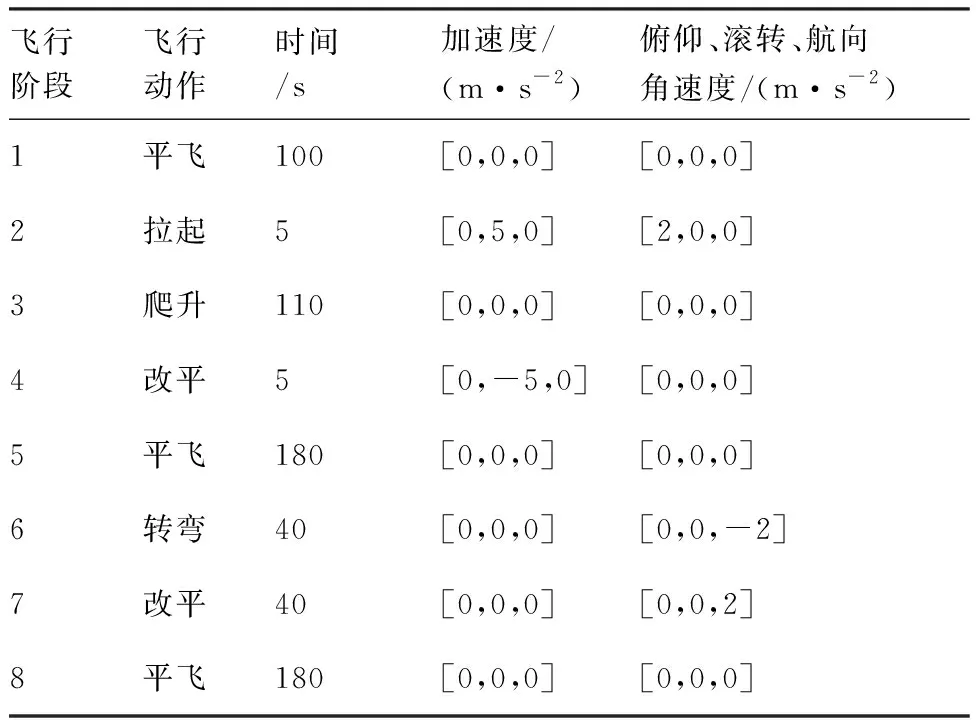
表1 無人機的軌跡參數Table 1 Trajectory parameter of UAV

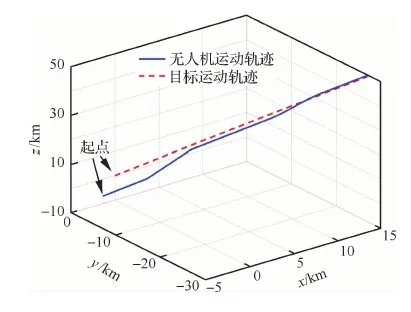
圖3 無人機與目標的相對位置示意圖Fig.3 Diagram of relative position between UAV and target

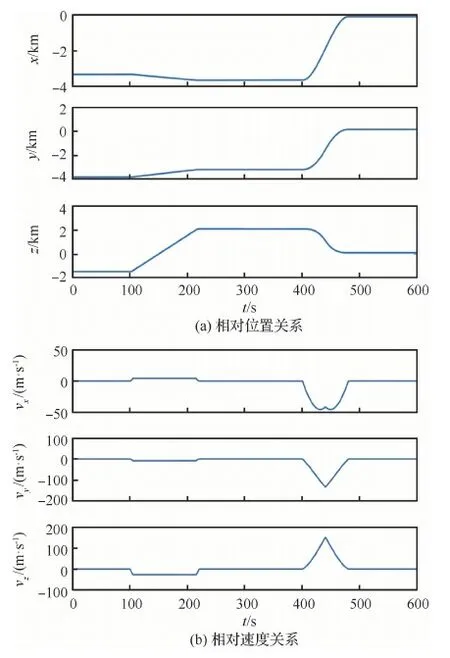
圖4 無人機與目標之間的相對位置和速度關系變化曲線Fig.4 Variation of relative position and velocity between UAV and target

4.2 僅含加性噪聲情況下的仿真與分析

本節在僅含加性噪聲的情況下，考察算法的精度。采用蒙特卡羅方法統計100次運行的結果，通過對每個時刻的100組數據取平均值繪制相對位置的誤差曲線如圖5(a) 所示，對100組數據求解RMSE值繪制對比曲線如圖5(b) 所示。由于LM本質是一種優化迭代過程的數值方法，可以有效地減少陷入局域極值的幾率，保證了全局的收斂性，因而也具有更好的穩定性。從圖5中初始階段的局部放大圖可以看出，在最初始的一段時間內，LM-IEKF算法的收斂速度是要介于IEKF和EKF之間的，相較于其他兩種算法，在性能表現上也顯得更為穩健。

圖6為相對速度的誤差曲線和RMSE對比曲線。從初始段的局部放大圖中可以看到，LM-IEKF算法具有更快的收斂速度，在5 s以內可以進入相對穩定的狀態，而另外兩種算法則要在10 s 左右。并且EKF和IEKF算法在初始段會

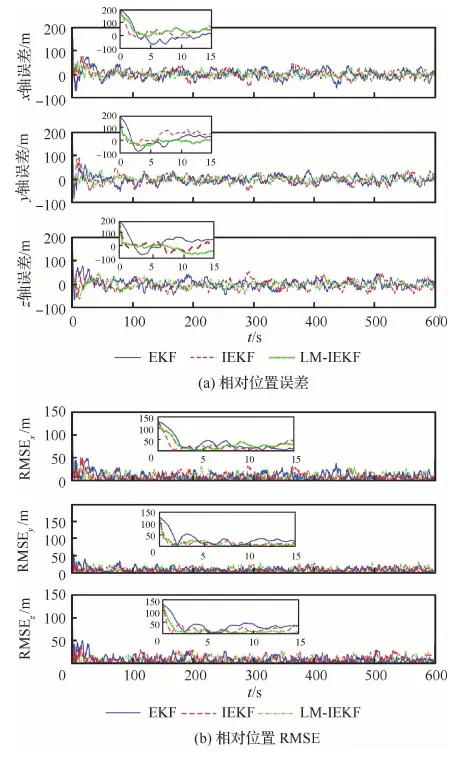
圖5 僅含加性噪聲情況下的相對位置誤差和RMSE曲線Fig.5 Errors and RMSE curves of relative position with additive noise only

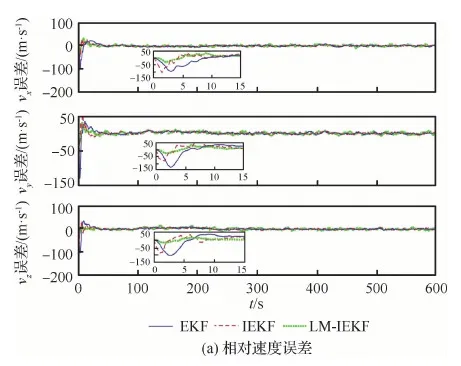
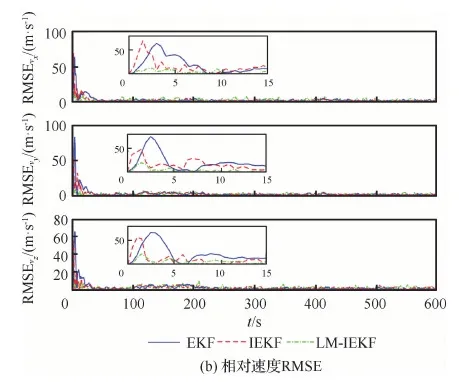
圖6 僅含加性噪聲情況下的相對速度誤差和RMSE曲線Fig.6 Errors and RMSE curves of relative velocity with additive noise only

產生較大的尖峰,相對速度誤差達到100 m/s，對比可知LM-IEKF算法具有較好的穩定性。

表2為3種算法對相對導航狀態的誤差統計，圖7(a)為根據表2數據繪制的相對位置精度柱狀圖，圖7(b)為相對速度精度柱狀圖。從圖7的柱狀圖可以看出，在相對位置和相對速度方面，LM-IEKF要優于其他2種算法。

本文提出的LM-IEKF算法相較于廣泛使用的EKF算法，在x、y、z三軸上，相對位置MAE分別減小了32%、30%和31%，相對速度MAE分別減小了25%、37%和17%。在RMSE方面，綜合相對位置精度提升了20%，綜合相對速度精度提升了46%。

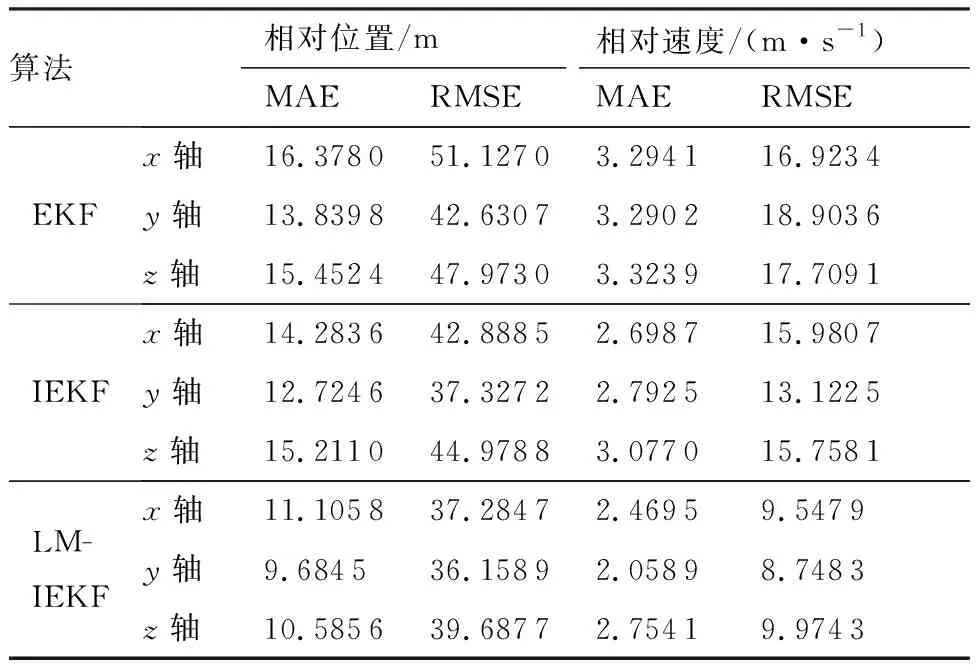
表2 僅含加性噪聲情況下的誤差統計Table 2 Error statistics with additive noise only

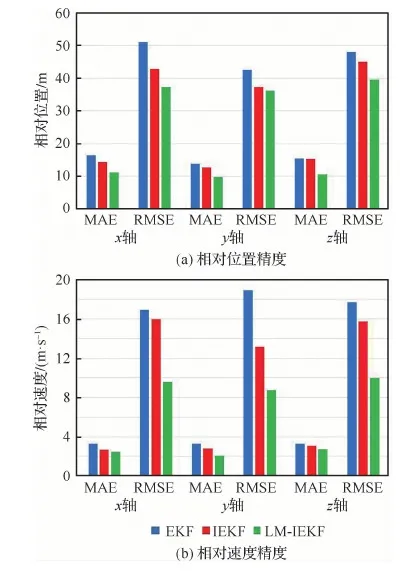
圖7 僅含加性噪聲情況的相對位置和速度精度柱狀圖Fig.7 Histogram of relative position and velocity accuracy with additive noise only

4.3 包含乘性噪聲情況下的仿真與分析

進一步討論本文提出的自適應量測噪聲修正算法對于乘性噪聲的修正效果，考慮到乘性噪聲與無人機和目標直線距離之間的線性關系，為了更好地反應出算法對乘性噪聲由小到大變化過程的適應性，乘性噪聲設置為均值是0.5，方差為4.9×10-3的高斯白噪聲[14-15]。Modified LM-IEKF算法的滑動窗口取10 s內的N組數據，N的大小取決于迭代的次數。采用蒙特卡羅方法運行100次進行統計比較。

從圖4(a)中可以看出，在x軸和y軸方向上，0～400 s之間為高乘性噪聲段，之后隨著無人機與目標之間距離的逐漸減小，乘性噪聲也逐漸減弱。在z軸方向上，100～200 s之間，乘性噪聲經歷了由強到弱再至強的變化過程，400 s后隨著相對位置逐漸接近，乘性噪聲也逐漸衰減。

圖8包含乘性噪聲情況下的相對位置誤差和RMSE曲線圖。從圖中可以看出，第2節中提出的LM-IEKF算法，有一定的改進效果。本文第3節 中提出的Modified LM-IEKF相較于前面的3種算法可以更好地統計量測噪聲，得到更高精度的相對導航狀態。

圖9為包含乘性噪聲情況下的相對速度誤差和RMSE曲線圖。由430～470 s之間的局部放大圖可以看到，在速度機動性較大的階段，Modified LM-IEKF相較于其他3種算法可以更快的做出響應，在y軸和z軸方向上更為明顯。

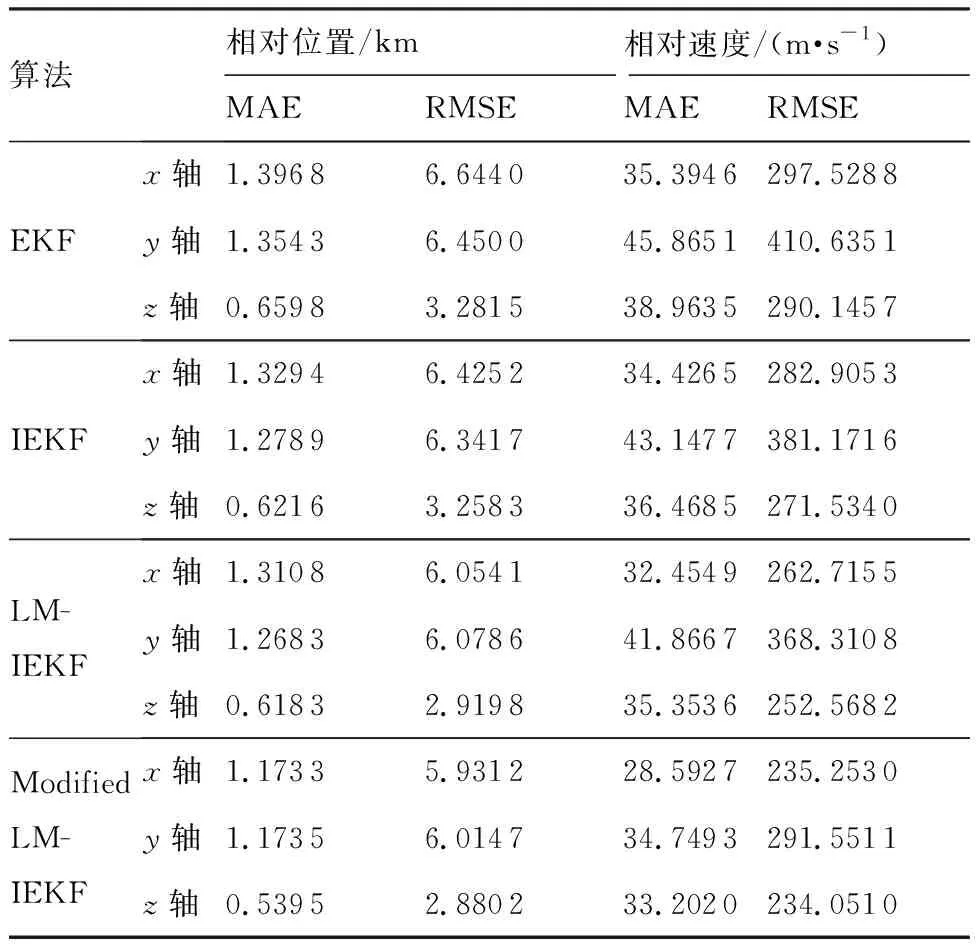
表3為4種算法在包含乘性噪聲情況下的精度對比情況。圖10為根據表3數據繪制的相對位置和相對速度精度柱狀圖。表中數據說明了Modified LM-IEKF算法相較于其他3種算法，在存在乘性噪聲污染的情況下，可以較大地提升性能。本文提出的Modified LM-IEKF算法相較于廣泛使用的EKF算法，在x、y、z三軸上，相對

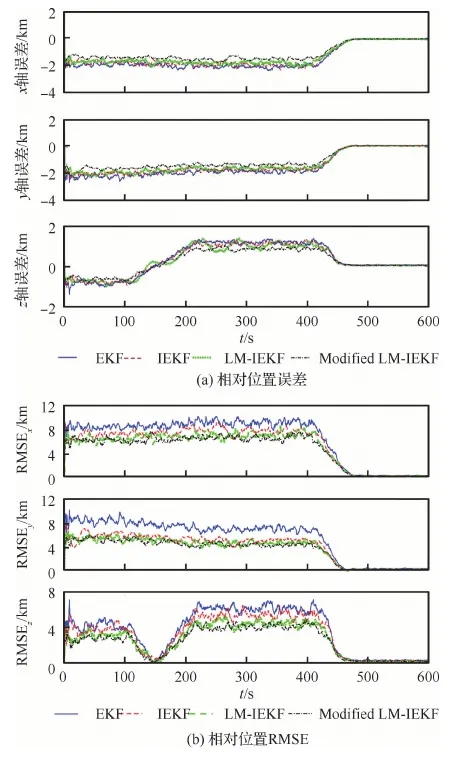
圖8 包含乘性噪聲的相對位置誤差和RMSE曲線Fig.8 Errors and RMSE curves of relative position containing multiplicative noise

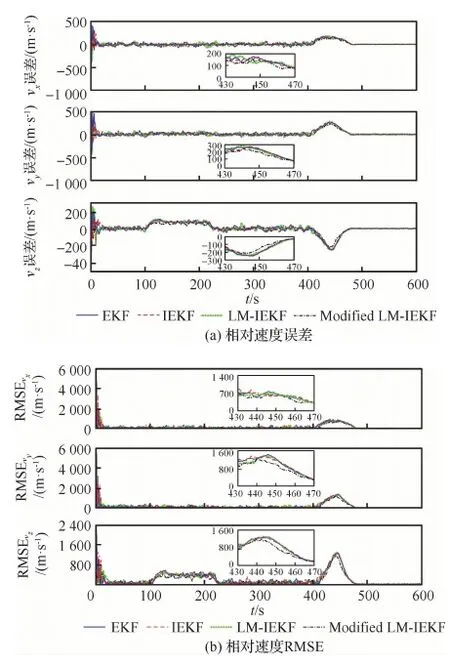
圖9 包含乘性噪聲的相對速度誤差和RMSE曲線Fig.9 Error and RMSE curves of relative velocity containing multiplicative noise

表3 包含乘性噪聲情況下的誤差統計Table 3 Error statistics containing multiplicative noise

算法相對位置/km相對速度/(m·s-1)MAERMSEMAERMSEEKFx軸1.39686.644035.3946297.5288y軸1.35436.450045.8651410.6351z軸0.65983.281538.9635290.1457IEKFx軸1.32946.425234.4265282.9053y軸1.27896.341743.1477381.1716z軸0.62163.258336.4685271.5340LM-IEKFx軸1.31086.054132.4549262.7155y軸1.26836.078641.8667368.3108z軸0.61832.919835.3536252.5682Modified LM-IEKFx軸1.17335.931228.5927235.2530y軸1.17356.014734.7493291.5511z軸0.53952.880233.2020234.0510

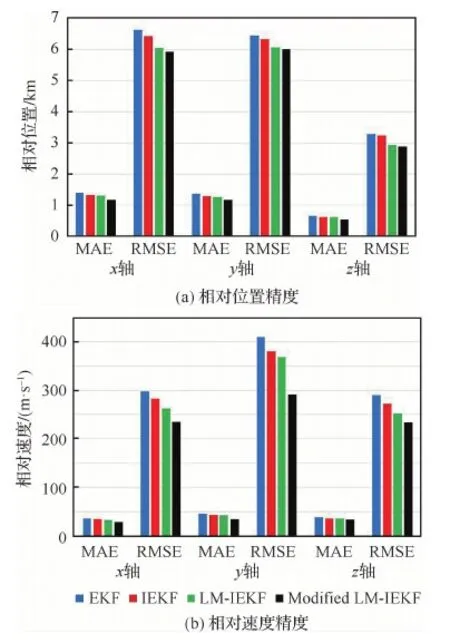
圖10 包含乘性噪聲情況下的相對位置和速度精度柱狀圖Fig.10 Histogram of relative position and velocity accuracy containing multiplicative noise

位置MAE分別減小了16%、13%和18%，相對速度MAE分別減小了34%、23%和14%。在RMSE方面，綜合相對位置精度提升了10%，綜合相對速度精度提升了23%。

5 結 論

1) 本文針對無人機與非合作目標之間的中遠距相對導航問題，提出了一種LM-IEKF相對狀態估計算法。該算法利用了Levenberg-Marquardt優化的思想改進IEKF中的迭代過程，以提高濾波器的精度和穩定性。通過計算對比分析結果可知：在僅含加性噪聲情況下，LM-IEKF算法相較于EKF、IEKF具有更好的性能。

2) 考慮到距離傳感器因信號相關特性所引入的乘性噪聲，進一步提出了基于量測噪聲自適應修正地Modified LM-IEKF算法。通過對比分析：在包含乘性噪聲的情況下，Modified LM-IEKF算法可以有效的在線估計量測噪聲，在提高相對導航狀態估計精度方面優于其他算法。與目前廣泛使用的EKF算法相比，在綜合相對位置精度上提高了10%，在綜合相對速度精度上提升了23%。

上述研究成果對于無人機在民用、軍用等領域的發展具有一定的參考價值。