基于擾動觀測器的機器人自適應神經網絡跟蹤控制研究

于欣波 賀威 薛程謙 孫永坤 孫長銀

在國內傳統制造業發展過程中,機器人技術的應用將極大程度地帶動傳統裝備制造業的轉型升級[1].機器人的應用可以降低生產成本、提高生產效率,替代人在復雜、危險工業環境中完成任務,可以從事程序化、高強度、易疲勞的工作.除工業領域外,機器人還在軍事、航天、消防救災、家庭、社會服務和醫療中得到廣泛應用[2?5].

機器人是一類典型的非線性、強耦合、時變多輸入多輸出系統[6?8],這種復雜系統給控制器設計帶來一定的難度.因為實際情況存在多種不確定因素,機器人系統難以獲取精確的動力學模型[9],通常會出現模型失配、模型完全未知等情況,此時基于模型的非線性控制策略將失效.另外,傳統控制策略通常對非線性系統進行了線性假設,而這種控制設計也將一定程度影響系統穩定性和控制精度.

神經網絡具有一致逼近和自適應能力,能夠起到非線性補償、參數辨識等作用[10?12],也可以作為控制器直接控制機器人系統,在機器人系統中得到廣泛應用[13?16].神經網絡的早期研究缺乏對機器人閉環系統穩定性分析,以梯度學習算法(Error back propagation,BP)為例,需要通過一定時間的離線訓練才能將神經網絡應用于機器人閉環系統中.反步法通過迭代設計與坐標變換[17],并設置虛擬鎮定變量,結合自適應控制,可以應用于含不確定參數的非線性系統并通過選取合適參數調整瞬態特性[18],實現漸近穩定或一致有界[19].

本文采用徑向基函數(Radial basis function,RBF)[20]作為神經網絡(Neural network,NN)[21]隱含層激活函數,通過RBF神經網絡估計控制器中不確定項,利用李雅普諾夫穩定性理論反推得到神經網絡權重自適應律,避免離線訓練,通過在線反饋系統輸入輸出數據,構造合適的神經網絡結構,使機器人系統達到跟蹤精度并滿足穩定性條件,實現系統誤差信號的半全局一致有界.

文獻[22]提出了一種基于神經網絡估計未知動態模型的自適應控制策略,并通過反向傳播算法對系統靜態和動態參數進行了調整.文獻[23]以雙臂機器人為研究平臺,利用神經網絡技術估計多機械臂協調控制中的不確定非線性項,以提高協調控制位置精度.文獻[24]提出了一種基于神經網絡的自適應阻抗控制策略,通過神經網絡補償機器人中的部分不確定項,在控制作用下使外界交互力呈現出給定的理想阻抗關系.在文獻[25]中,神經網絡技術被應用于補償一種欠驅動輪式移動機器人動力學模型,解決一類自平衡移動小車的跟蹤控制問題,并基于擾動觀測器提出了一種魯棒跟蹤控制策略.除神經網絡具有一致逼近能力外,模糊控制對任意非線性系統也具有很好的擬合效果,文獻[26]利用模糊控制設計了一種含擾動觀測器的外骨骼控制系統,通過實驗驗證了控制器有效性.大多數文獻提出的控制方法在線計算量大,針對不確定性較大的機器人系統控制難度較高,并且對于考慮非參數的不確定系統控制研究較少.

擾動觀測器被廣泛應用于處理非線性系統中的不確定擾動[27?29],設計擾動觀測器的目的是不依靠附加的力傳感器來估計未知不確定擾動[30].文獻[31]利用擾動觀測器處理機器人系統的摩擦力補償問題,并通過仿真得到驗證.在文獻[32]中,擾動觀測器被用來處理非匹配不確定性帶來的擾動.文獻[33]設計了一種含有擾動觀測器的自適應神經網絡控制策略,以解決機器人系統中的時滯效應.如果在控制器設計過程中不考慮未知擾動帶來的影響,將會在一定程度上影響機械臂跟蹤精度.大多數研究多結合非線性系統設計擾動觀測器,對于機器人系統利用反推方法設計擾動觀測器并且將理論方法應用到實際機器人系統的研究較少.

近幾年提出的神經網絡控制方法結合傳統自適應控制、反演控制能夠解決含有線性參數的不確定非線性系統,但神經網絡難以處理含有非參數的系統不確定性.本文與其他方法不同的創新點是:本文主要結合自適應神經網絡和擾動觀測器同時解決系統模型未知部分和系統未知擾動,通過RBF神經網絡在線學習不確定模型并根據李雅普諾夫函數反推設計權重自適應律,證明了閉環系統誤差信號半全局一致有界.本文同時將跟蹤控制算法應用于仿真與實際Baxter機器人中,通過兩臺計算機互相配合,即一臺計算神經網絡未知補償量,一臺通過用戶數據報協議(User datagram protocol,UDP)接收信息并產生Baxter機器人控制信號,一定程度上提升整個系統的運算和響應能力,并通過實驗對比PD控制驗證了所提出控制算法的有效性和優勢.

以下幾章將對本文所提出的控制算法進行詳細介紹與分析.文章具體安排如下:第1節通過D-H(Denavit-Hartenberg)建模方法對Baxter機器人運動學進行分析,通過Lagrange-Euler方法建立機器人動力學模型;第2節考慮動力學模型已知的情況,設計一種基于模型的通用跟蹤控制器和擾動觀測器并對閉環系統進行穩定性分析;第3節考慮機器人模型未知的情況,提出一種基于擾動觀測器的自適應神經網絡全狀態反饋跟蹤控制策略,并通過構造李雅普諾夫函數分析機器人系統穩定性;第4節通過數值仿真驗證所提出的控制算法的有效性與通用性,仿真考慮了不同關節連接方式的機器人,分別利用機器人工具箱和數值仿真驗證跟蹤控制算法的有效性和控制精度;第5節簡述了Baxter機器人的硬件及軟件結構,將控制算法應用于Baxter機器人實驗平臺上并與比例微分(Proportion derivative,PD)控制進行對比以驗證所提出控制算法的跟蹤精度.

1 運動學與動力學分析

1.1 Baxter機器人運動學分析

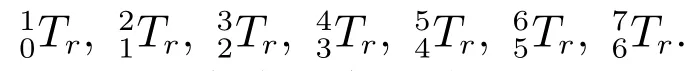
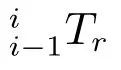
其中,c代表余弦運算cos,s代表正弦運算sin.di表示平移距離,αi表示扭轉角,ai表示長度,θi表示關節角度.

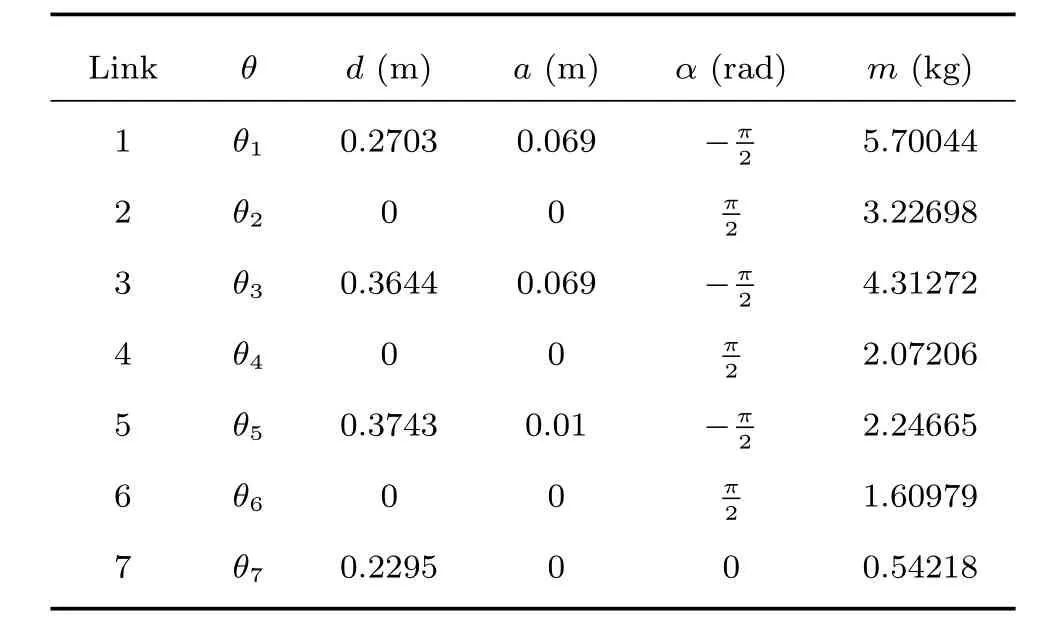
表1 Baxter機器人D-H參數和連桿質量Table 1 D-H parameter and link mass of Baxter robot

通過Baxter機器人制造商Rethink robotics在Github網站上提供的相關信息,可以從中獲取剛性連桿i的質量如表1所示,其中連桿慣性矩陣、轉動慣量以及相對坐標中心位置都可以從中獲得.

1.2 機器人動力學分析

通過拉格朗日動力學方程,建立機械臂n關節通用動力學模型:

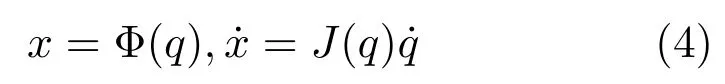
機械臂逆向運動學可由下式關系表示:

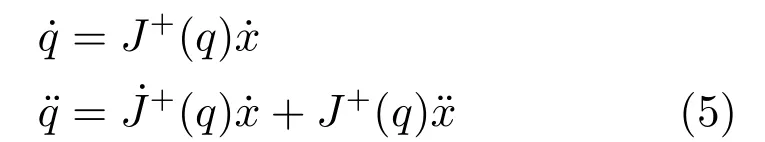
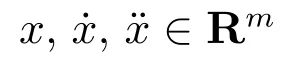
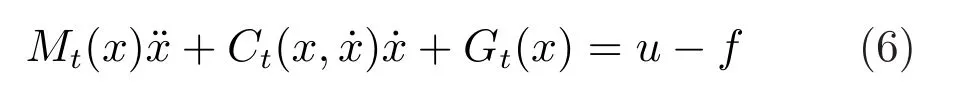
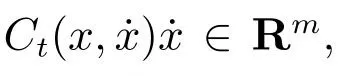
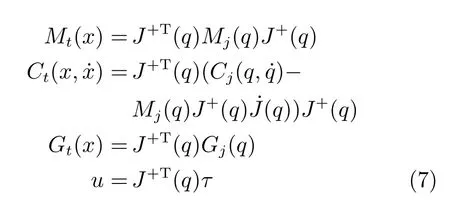
以下為本文利用的相關定義、引理與性質:

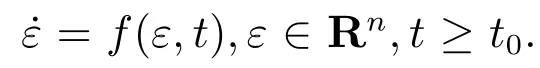
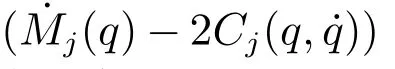
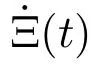
2 含擾動觀測器的模型控制器設計

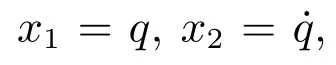
定義xd為關節空間期望軌跡向量,定義狀態誤差如下式:

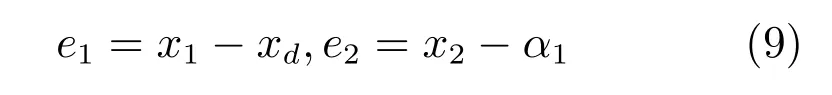
為設計擾動觀測器我們定義一個輔助變量e3表示為:

其中,%(e2)代表非線性函數向量,同時我們定義式(9)中α1為虛擬鎮定信號,e1為角度誤差,e2為虛擬速度誤差,其中,α1定義如下:

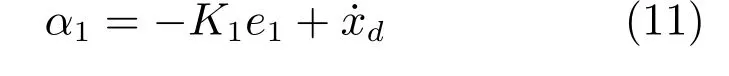
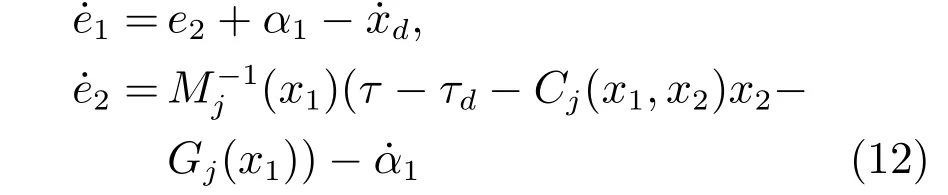
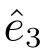
通過式(15)可以得到:

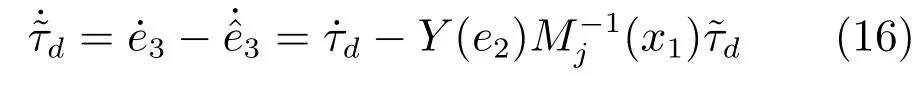
由以上分析設計基于模型的控制器τ0為:

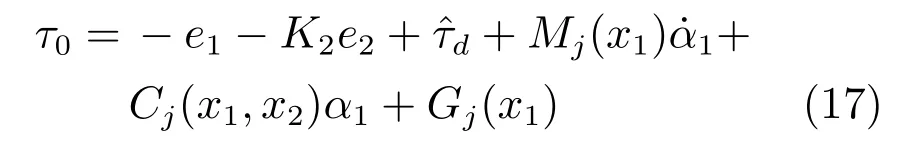
下面對系統穩定性進行分析,構造如下李雅普諾夫函數V1:

將模型控制器τo代入上式可得:

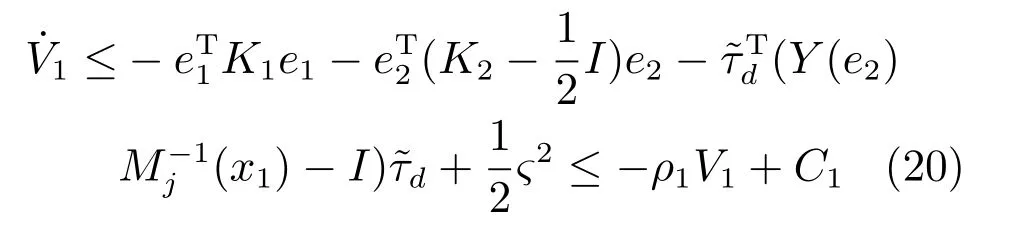
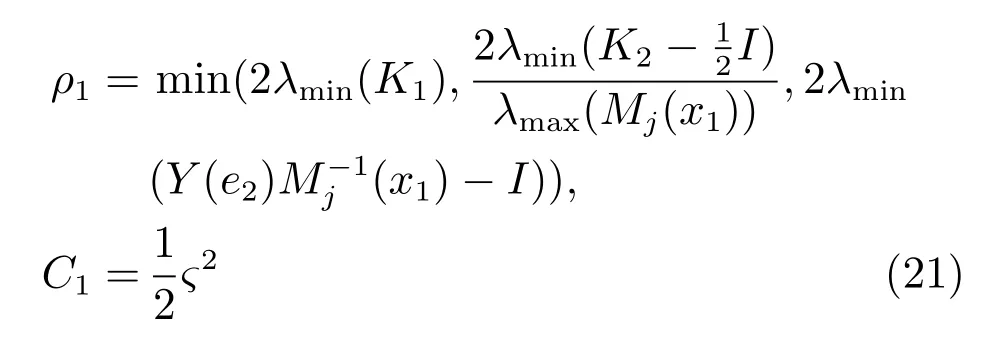
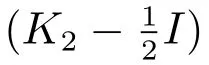
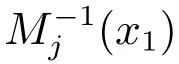
3 含擾動觀測器的自適應神經網絡控制器設計

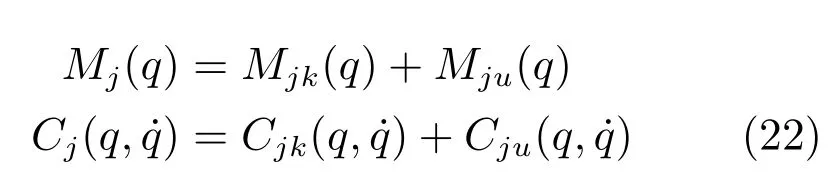
利用神經網絡一致逼近性能,設計一種在線自適應神經網絡控制器以補償未知動力學模型參數.自適應神經網絡控制器τf設計為:

式中,ψ(Z)代表RBF神經網絡徑向基函數,代表神經網絡權重估計,其中,$?代表神經網絡實際最優權重,最優權重是為便于推導分析人為構造的,其定義如下:

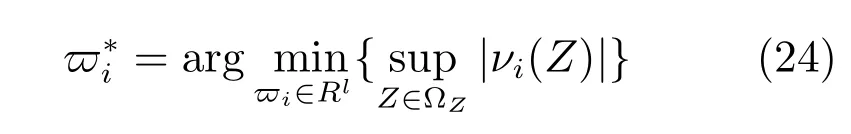
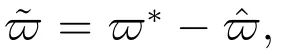
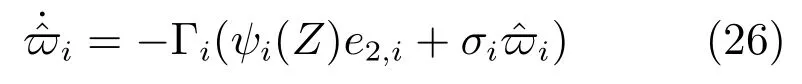
式中,σi為小的正常數,Γi為正定對稱矩陣.把式(25)代入式(12)可得:

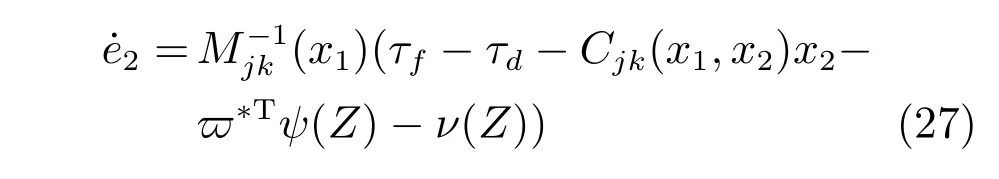
同模型控制類似,我們定義輔助變量e4為:

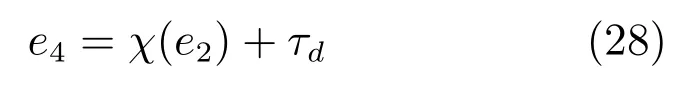
對e4求導可得:

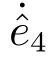
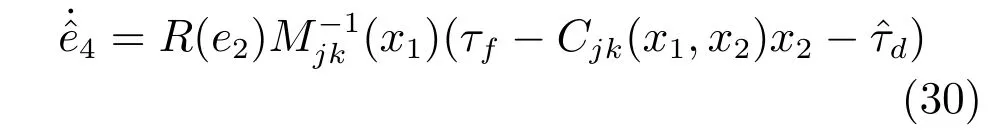
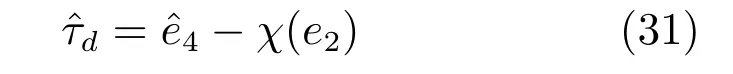
通過式(28)和(31)可以得出:

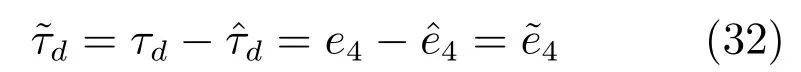
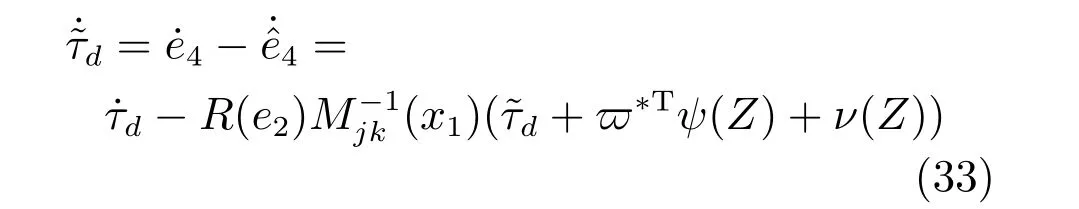
下面對神經網絡控制器的閉環系統進行穩定性分析,構造如下李雅普諾夫函數V2:

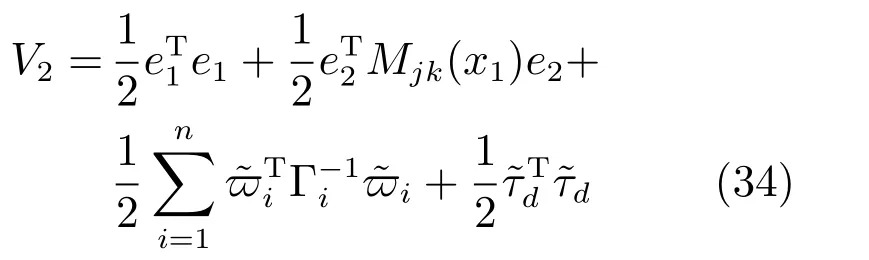
對V2求導,并將神經網絡控制器代入可得到如下式所示結果:

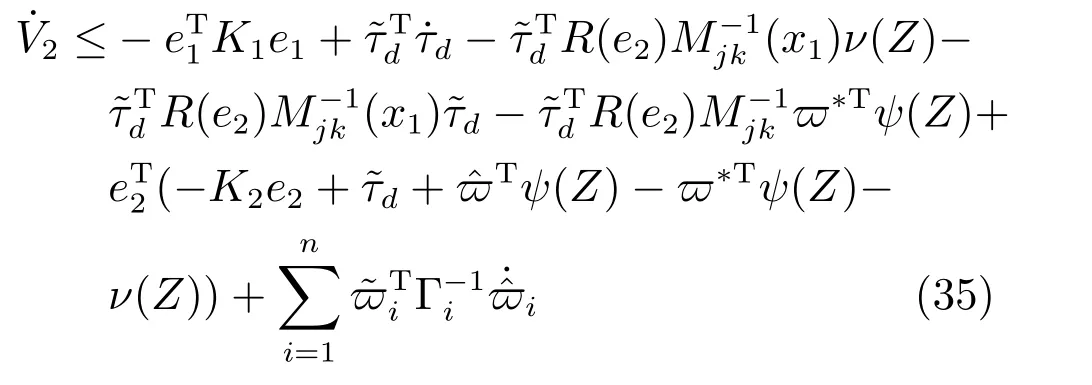
利用如下不等式性質:

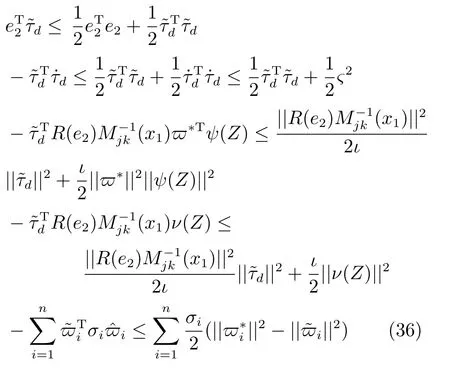
可以得到:

式中,ρ2和C2分別為:

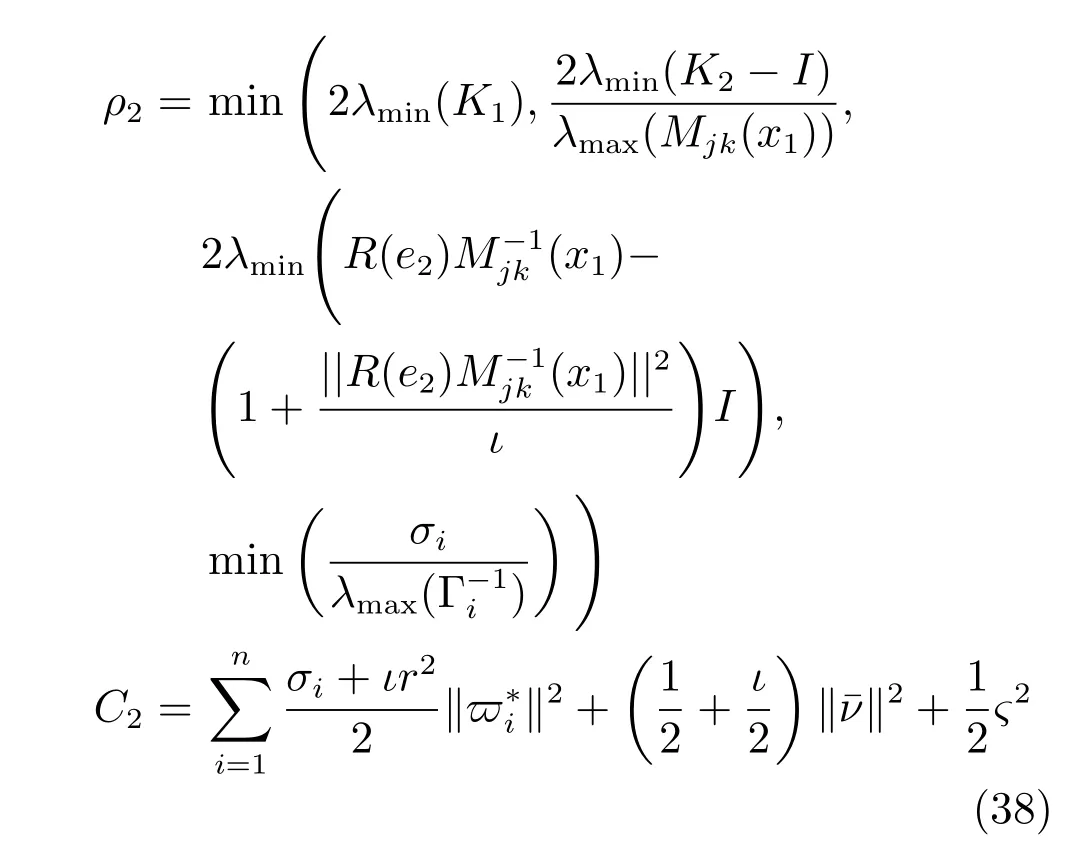
為使ρ2>0,控制增益需滿足以下條件:

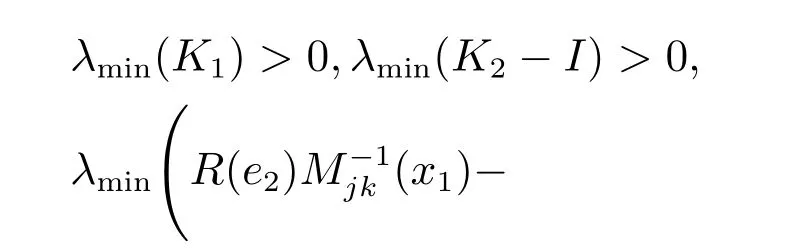
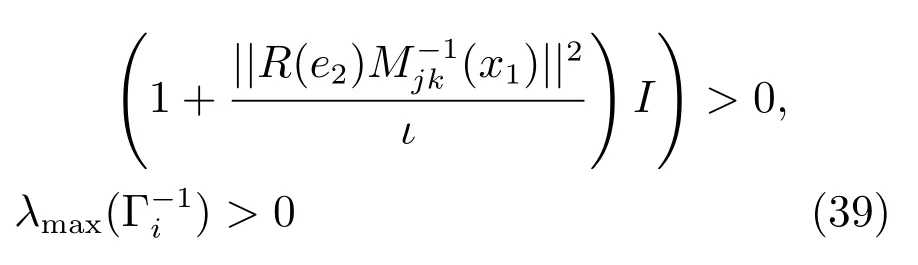
通過以上分析,我們可以證明誤差e1,e2,和為半全局一致有界.

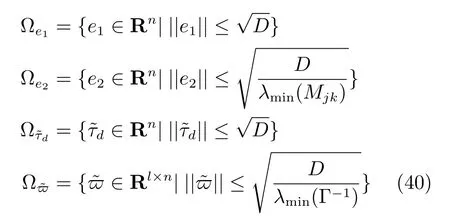
其中,D=2(V2(0)+C2/ρ2),l為神經網絡節點數,ρ2和C2為正常數.

證明.在式(37)左右兩端乘以eρ2t,可以得到:

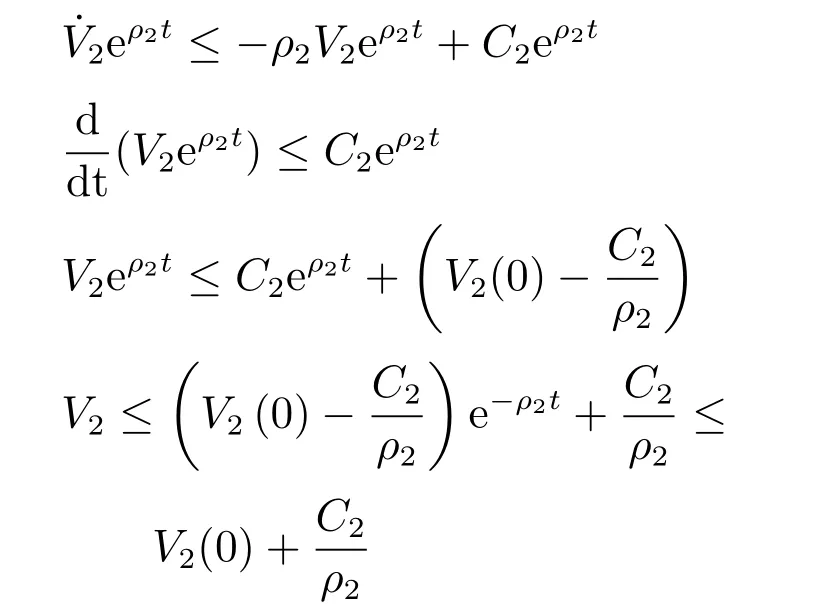
由以上分析可以得出:

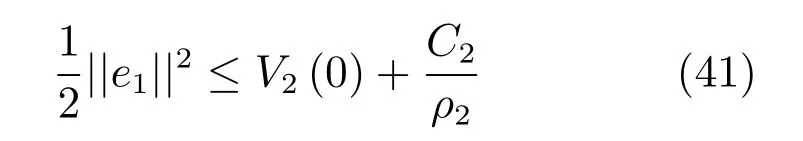
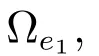
4 數值仿真

4.1 3旋轉關節機器人仿真

本節通過Matlab機器人工具箱(Robotic toolbox)程序對具有3旋轉關節的機器人進行數值仿真.如圖1所示,剛性連桿1質量與長度:mt1=0.5kg,lt1=0.114m;剛性連桿2質量與長度:mt2=0.5kg,lt2=0.144m;剛性連桿3質量與長度:mt3=1kg,lt3=0.241m.初始關節角矩陣設置為[0.0714rad;1.6718rad;?1.7432rad].設置任務空間期望軌跡為:

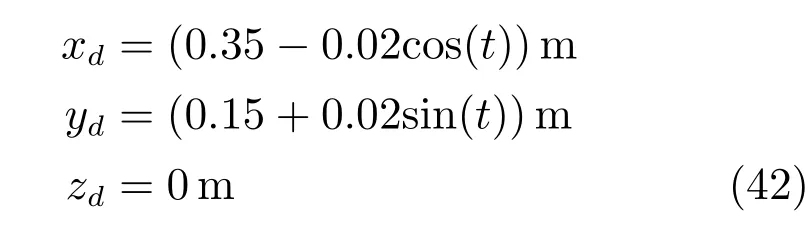
其中,RBF參數節點數選擇為28=256,鎮定參數為0.02,正定增益矩陣為Γi=10I256×256.神經網絡中心選擇為 [?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1],其中控制增益K1=diag{40,40,40},K2=diag{30,30,30},擾動設置為[0.02sin(t)+0.06,0.01cos(t)+0.02,0]T,擾動觀測器χ(e2)設置為[25e21,25e22,25e23]T.圖2、3分別為關節空間、任務空間中3關節神經網絡控制與PD控制跟蹤對比圖.圖4為任務空間中神經網絡與PD控制對比效果圖,圖5為神經網絡控制器控制輸入.由上圖可知,所提出的控制算法可以保證跟蹤誤差收斂到較小的零域內,較PD控制而言,所提出的神經網絡控制具有更好的跟蹤控制效果.

4.2 2旋轉關節1伸長關節機器人仿真

本節通過Matlab數值仿真對具有2旋轉關節1伸長關節的機器人系統進行仿真.其中剛性連桿1質量與長度:mt1=2.0kg,lt1=0.3m;剛性連桿2質量與長度:mt2=2.0kg,lt2=0.4m;剛性連桿3質量與長度:mt3=1.0kg,lt3=0.25m.初始狀態矩陣為[0.5rad;0.9rad;0.4m].設置期望跟蹤軌跡為:

其中,RBF參數節點數為212,鎮定參數為0.02,正定增益矩陣為Γi=10I212×212.神經網絡中心選擇為 [?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1]×[?1,1],其中控制增益K1=diag{6,6,6},K2=diag{12,12,12}.圖6,8,10分別為3關節含擾動觀測器的神經網絡控制與不含擾動觀測器角度跟蹤控制對比圖,圖7,9,11分別為3關節含擾動觀測器的神經網絡控制與不含擾動觀測器速度跟蹤控制對比圖.真實擾動設置為[sin(t)+1,2cos(t)+0.5,2sin(t)+1]T.擾動觀測器χ(e2)設置為[25e21,25e22,25e23]T.

圖1 3旋轉關節自由度機器人Robotic toolbox中的模型Fig.1 Model of 3 revolute joint robot in robotic toolbox

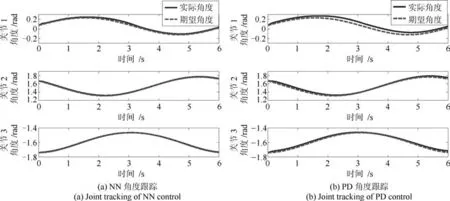
圖2 NN與PD控制角度跟蹤Fig.2 Joint tracking of NN and PD control

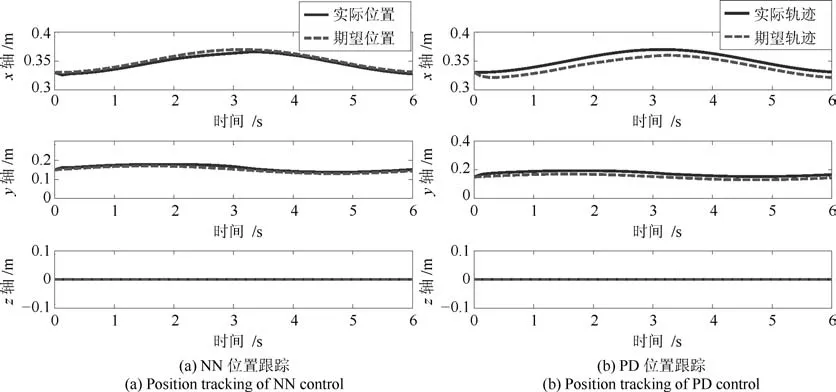
圖3 NN與PD控制位置跟蹤Fig.3 Position tracking of NN and PD control

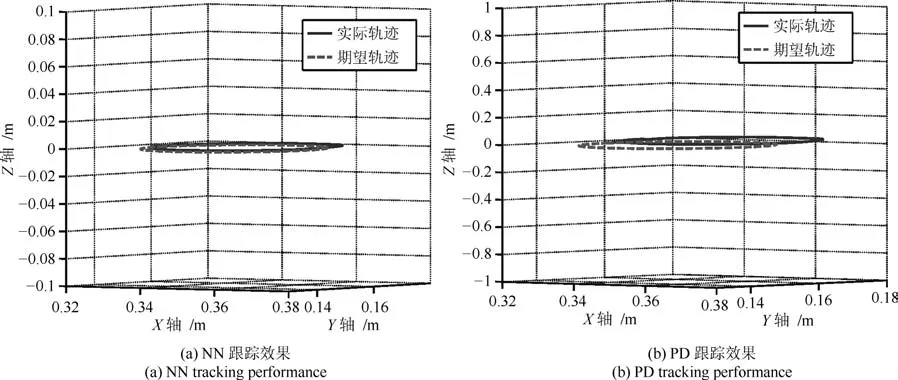
圖4 NN與PD軌跡跟蹤效果Fig.4 NN and PD trajectory tracking performance

圖5 NN控制輸入Fig.5 NN control input

由上圖可知,所提出的帶擾動觀測器的控制算法可以保證跟蹤誤差收斂到較小的零域內,較不加擾動觀測器控制而言,所提出的帶擾動觀測器神經網絡控制器具有更好的跟蹤控制效果.圖12為擾動觀測器與真實擾動誤差對比圖,圖13為控制輸入對比圖,圖14為神經網絡估計權值與權值估計誤差圖,圖15為神經網絡逼近函數與被逼近函數.由圖12、14和15可知,擾動觀測器觀測誤差和神經網絡估計誤差都將收斂到較小的零域內.

圖6 關節1含擾動觀測器和不加擾動觀測器角度跟蹤控制Fig.6 Joint 1 angle tracking control with and without disturbance observer

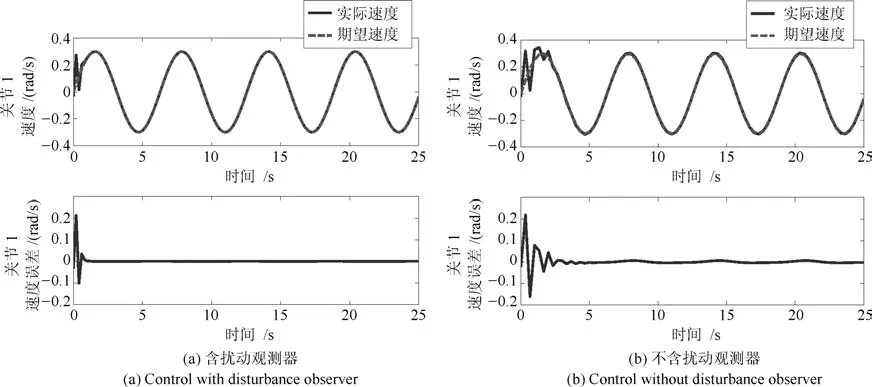
圖7 關節1含擾動觀測器和不加擾動觀測器速度跟蹤控制Fig.7 Joint 1 velocity tracking control with and without disturbance observer

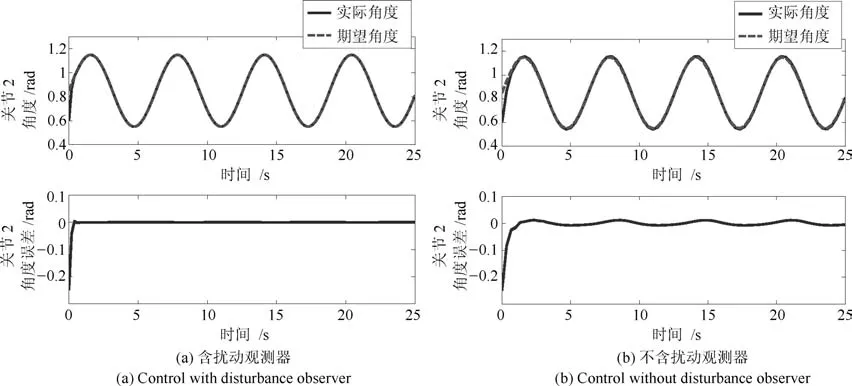
圖8 關節2含擾動觀測器和不加擾動觀測器角度跟蹤控制Fig.8 Joint 2 angle tracking control with and without disturbance observer

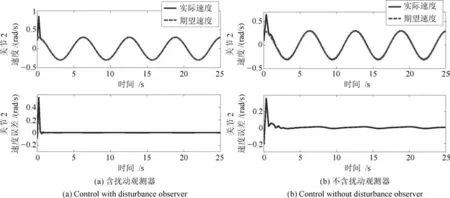
圖9 關節2含擾動觀測器和不加擾動觀測器速度跟蹤控制Fig.9 Joint 2 velocity tracking control with and without disturbance observer

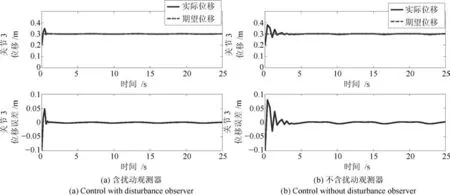
圖10 關節3含擾動觀測器和不加擾動觀測器角度跟蹤控制Fig.10 Joint 3 angle tracking control with and without disturbance observer

圖11 關節3含擾動觀測器和不加擾動觀測器速度跟蹤控制Fig.11 Joint 3 velocity tracking control with and without disturbance observer

圖12 擾動與擾動觀測誤差Fig.12 Disturbance and disturbance observer error

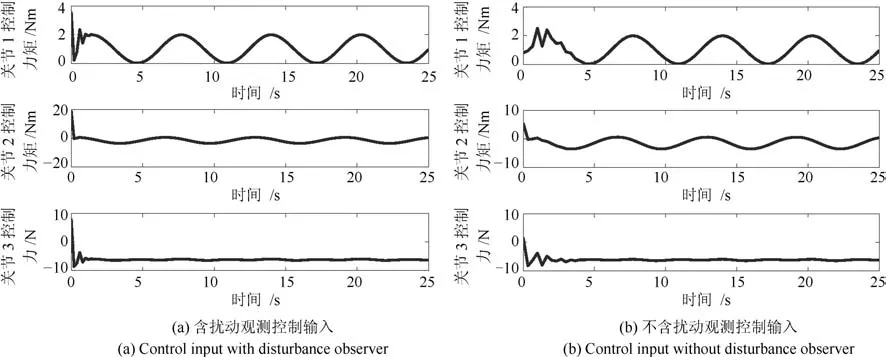
圖13 控制輸入Fig.13 Control input

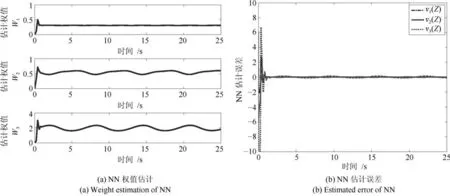
圖14 NN權值估計與誤差Fig.14 Weight estimation and error of NN

圖15 逼近函數與被逼近函數Fig.15 Approximation and approximated function

5 基于Baxter機器人的跟蹤實驗驗證

本文基于Baxter機器人對自適應神經網絡跟蹤控制策略進行實驗驗證.Baxter機器人是美國Rethink robotics公司研發的一款雙臂機器人[36],其單機械臂是一種具有七自由度的冗余柔性關節機械臂[37].Baxter機械臂存在的摩擦力等未知擾動也會影響到機器人的控制精度.因此,對于Baxter機器人需要提高其定位精度以完成精確的跟蹤任務[38].圖16為Baxter機器人結構示意圖.通過移動底座支撐機器人本體,機器人手臂采用旋轉關節連接剛性連桿,關節處采用彈性制動器連接,即通過電機、減速器串聯彈簧帶動負載,在人機協作或外部沖擊下起到保護人或機器人本體的作用.柔性關節還可通過霍爾效應檢測角度偏差,由于彈簧具有固定剛度,通過胡克定律可檢測關節處力矩,即在Baxter關節處都具有力矩傳感器.手臂前后端通過26W 和63W 伺服電機驅動,通過14bit編碼器實現關節角度的讀取.Baxter機器人為基于ROS(Robot operating system)操作系統的開源機器人,通過Linux平臺運行,用戶可通過網絡與機器人內部計算機互聯讀取信息或發送指令,或通過SSH(Secure shell)遠程控制在內部計算機運行相關程序.利用Baxter相關的SDK(Software development kit),通過ROS的API(Application programming interface)可以實現對Baxter機器人的信息讀取與實時控制.Baxter中的SDK可以提供相關函數接口與重要工具:如Gazebo仿真器及Moveit移動軟件包等.Baxter機器人在力矩控制模式下,還需設置補償力矩以抵消機械臂重力和肩關節支撐彈簧形變帶來的影響.

本節通過Baxter機器人實現機器人軌跡跟蹤實驗.圖17為Baxter機器人實驗平臺.計算機A通過Windows MATLAB simulink模塊計算神經網絡未知補償量并通過UDP傳輸至另一臺用于接收機器人狀態信號并提供控制信號的計算機B中.計算機B利用Ubuntu 14.04 LTS平臺下的Baxter RSDK(Robot operating system SDK)實現對Baxter機器人的編程與控制.其中RBF神經網絡參數節點數為73,鎮定參數為0.02,正定增益矩陣Γi=500I.協方差為0.75,其中控制增益K1=diag{17.7,20,15.7,22,20.3,12.6,15},K2=diag{2.1,2.2,1.2,2,5.1,10.1,4.5}.利用Moveit軟件令Baxter機器人單臂移動一段距離,通過實時位置反饋信息,記錄下移動過程中各關節軌跡.之后通過設計控制器令關節跟蹤這條期望軌跡,并將所提出的控制方法與PD控制對比軌跡跟蹤效果.表2所示為Baxter機器人PD控制參數.圖18～24分別為Baxter機器人S0,S1,E0,E1,W0,W1,W2關節含擾動觀測器的神經網絡與PD控制角度跟蹤效果對比圖.圖25為Baxter機器人七關節神經網絡控制輸入.由圖18～24通過與PD控制對比可以得出,所提出的控制算法與PD控制相比具有更好的跟蹤控制效果.

圖16 Baxter機器人系統結構:1.肩S0關節;2.肩S1關節;3.肘E0關節;4.肘E1關節;5.腕W0關節;6.腕W1關節;7.腕W2關節;8.聲納傳感器;9.面部攝像頭;10.顯示屏;11.末端攝像頭;12.末端抓手;13.操作旋鈕;14.柔性關節;15.肩關節支撐彈簧;16.吸盤Fig.16 The system structure of Baxter robot:1.shoulder joint S0;2.shoulder jointS1;3.elbow jointE0;4.elbow jointE1;5.wrist jointW0;6.wrist jointW1;7.wrist jointW2;8.sonar sensor;9.facial camera;10.screen;11.end-effector camera;12.gripper;13.operating knob;14.flexible joint;15.S1shoulder support spring;16.sucker

圖17 Baxter機器人實驗平臺Fig.17 Experimental platform of Baxter robot

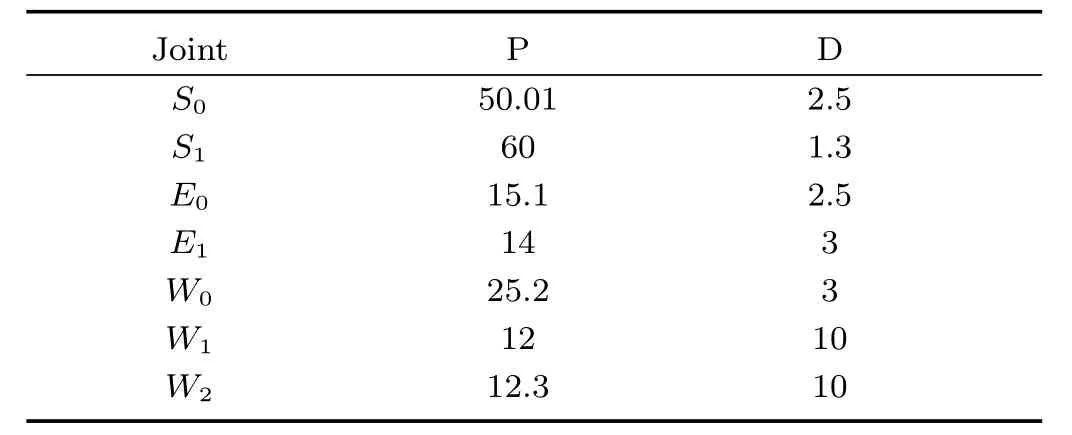
表2 Baxter機器人PD控制參數Table 2 PD control parameter of Baxter robot

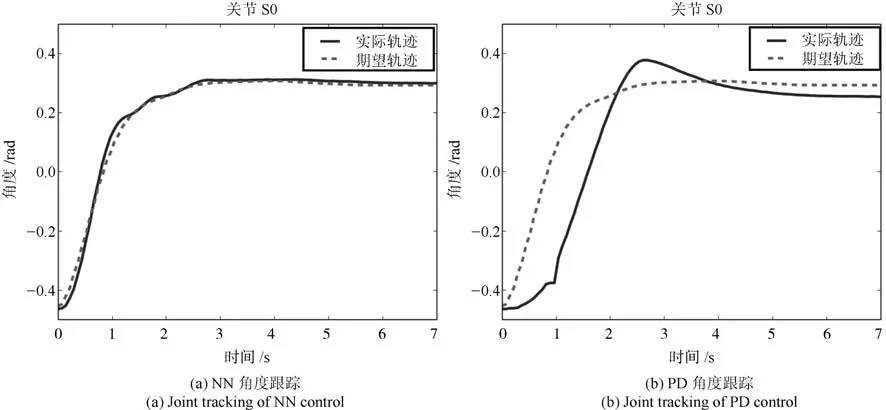
圖18 NN與PD控制S0關節角度跟蹤Fig.18 S0 joint tracking of NN and PD control

圖19 NN與PD控制S1關節角度跟蹤Fig.19 S1 joint tracking of NN and PD control

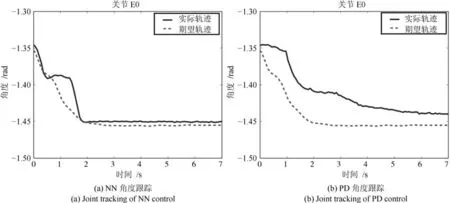
圖20 NN與PD控制E0關節角度跟蹤Fig.20 E0 joint tracking of NN and PD control

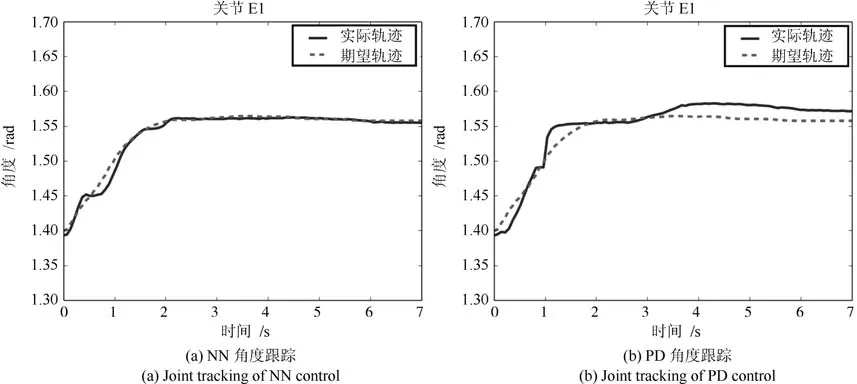
圖21 NN與PD控制E1關節角度跟蹤Fig.21 E1 joint tracking of NN and PD control

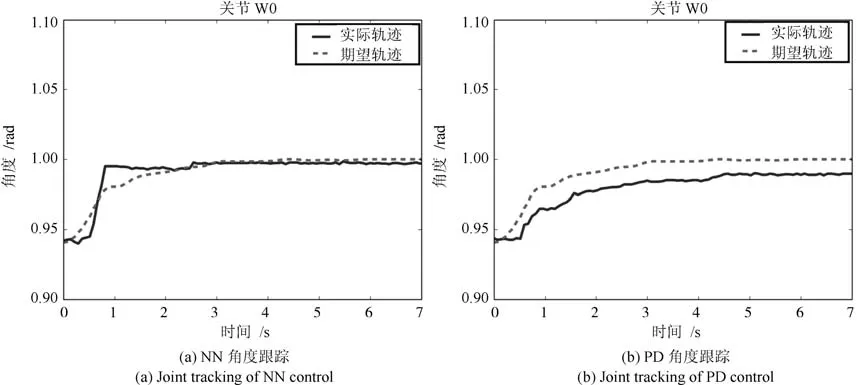
圖22 NN與PD控制W0關節角度跟蹤Fig.22 W0 joint tracking of NN and PD control

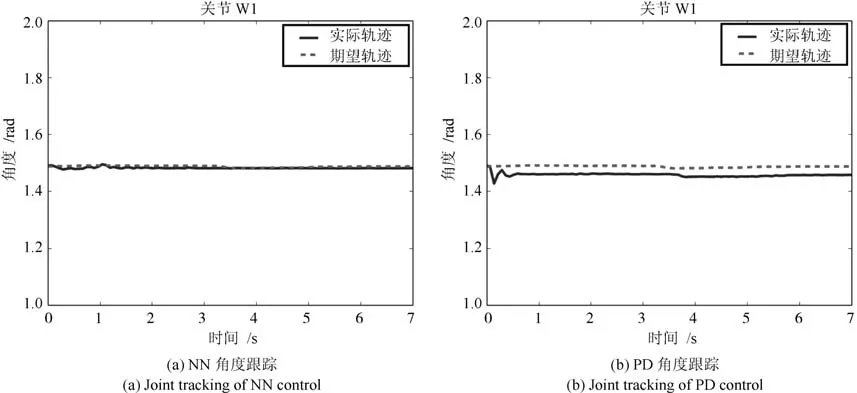
圖23 NN與PID控制W1關節角度跟蹤Fig.23 W1 joint tracking of NN and PID control

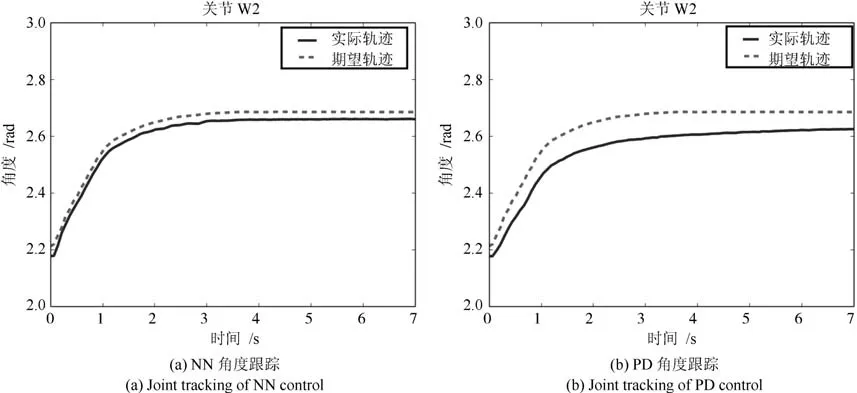
圖24 NN與PD控制W2關節角度跟蹤Fig.24 W2 joint tracking of NN and PD control

圖25 Baxter機器人NN控制輸入Fig.25 NN control input to Baxter robot

6 結論

本文提出了一種基于擾動觀測器的自適應神經網絡跟蹤控制策略,以解決機器人動力學模型未知問題并提升系統魯棒性.針對模型已知的情況,通過研究機器人運動學和動力學模型,提出了剛體機械臂通用模型跟蹤控制策略;針對動力學模型未知情況下,設計了基于全狀態反饋的自適應RBF神經網絡跟蹤控制器,并通過設計擾動觀測器補償系統中的未知擾動.通過選擇合適的增益參數可以將跟蹤誤差收斂到零域,并利用李雅普諾夫理論證明所提出的控制策略能使閉環系統誤差信號半全局一致有界.最后通過對比仿真證明所提出算法的有效性并且將控制算法在Baxter機器人平臺上進行驗證.