基于事件觸發的三階離散多智能體系統一致性分析

董滔 李小麗 趙大端

近些年來,由于多智能體協同控制在編隊控制[1]、機器人網絡[2]、群集行為[3]、移動傳感器[4?5]等方面的廣泛應用,多智能體系統的協同控制問題受到了眾多研究者的廣泛關注.一致性問題是多智能體系統協同控制領域的一個關鍵問題,其目的是通過與鄰居之間的信息交換,使所有智能體的狀態達成一致.迄今為止,對多智能體一致性的研究也已取得了豐碩的成果,根據多智能體的動力學模型分類,主要可以將其分為以下4種情形:一階[6?9]、二階[10?13]、三階[14?15]、高階[16?18].

在實際應用中,由于CPU處理速度和內存容量的限制,智能體不能頻繁地進行控制以及與其鄰居交換信息.因此,事件觸發控制策略作為減少控制次數和通信負載的有效途徑,受到了越來越多的關注.到目前為止,對事件觸發控制機制的研究也取得了很多成果[19?23].Xiao等[19]基于事件觸發控制策略,解決了帶有領航者的離散多智能體系統的跟蹤問題.通過利用狀態測量誤差并且基于二階離散多智能體系統動力學模型,Zhu等[20]提出了一種自觸發的控制策略,該策略使得所有智能體的狀態均達到一致.Huang等[21]研究了基于事件觸發策略的Lur'e網絡的跟蹤問題.針對不同的領航者–跟隨者系統,Xu等[22]提出了3種不同類型的事件觸發控制器,包含分簇式控制器、集中式控制器和分布式控制器,以此來解決對應的一致性問題.然而,大多數現有的事件觸發一致性成果集中于考慮一階多智能體系統和二階多智能體系統,很少有成果研究三階多智能體系統的事件觸發控制問題,特別是對于三階離散多智能體系統,成果更是少之又少.所以,設計相應的事件觸發控制協議來解決三階離散多智能體系統的一致性問題已變得尤為重要.

本文研究了基于事件觸發控制機制的三階離散多智能體系統的一致性問題,文章主要有以下三點貢獻:

1)利用位置、速度和加速度三者的測量誤差,設計了一種新穎的事件觸發控制機制.

2)利用不等式技巧,分析得到了保證智能體漸近收斂到一致狀態的充分條件.與現有的事件觸發文獻[19?22]不同的是,所得的一致性條件與通信拓撲的Laplacian矩陣特征值和系統的耦合強度有關.

3)給出了排除類Zeno行為的參數條件,進而使得事件觸發控制器不會每個迭代時刻都更新.

1 預備知識

1.1 代數圖論

智能體間的通信拓撲結構用一個有向加權圖來表示,記為G={?,?,?}.其中,?={1,2,···,n}表示頂點集,???×?表示邊集,?=(aij)n×n稱作鄰接矩陣,aij表示邊(j,i)∈?的權值.當(j,i)∈?時,有aij>0;否則,有aij=0.aij>0表示智能體i能收到來自智能體j的信息,反之則不成立.對任意一條邊j,節點j稱為父節點,節點i則稱為子節點,節點i是節點j的鄰居節點.假設通信拓撲中不存在自環,即對任意i∈?,有aii=0.

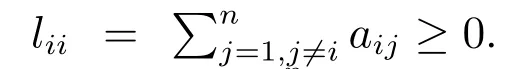
1.2 模型描述

考慮多智能體系統由n個智能體組成,其通信拓撲結構由有向加權圖G表示,其中每個智能體可看作圖G中的一個節點,每個智能體滿足如下動力學方程:

其中,xi(k)∈R表示位置狀態,vi(k)∈R表示速度狀態,zi(k)∈R表示加速度狀態,ui(k)∈R表示控制輸入.

基于事件觸發控制機制的控制器協議設計如下:

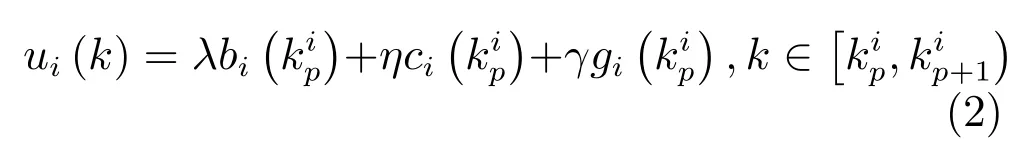
其中,λ>0,η>0,γ>0表示耦合強度,

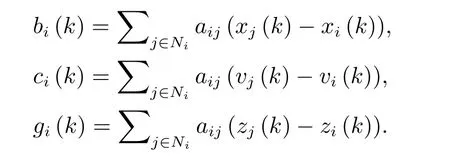
觸發時刻序列定義為:

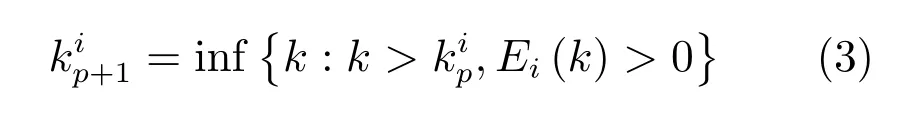
Ei(k)為觸發函數,具有以下形式:

再結合式(1)和式(2)可得到:

定義1.對于三階離散時間多智能體系統(1),當且僅當所有智能體的位置變量、速度變量、加速度變量滿足以下條件時,稱系統(1)能夠達到一致.

2 一致性分析主要結果

假設κ是矩陣Q1的特征值,μi是L的特征值,則有如下等式成立:

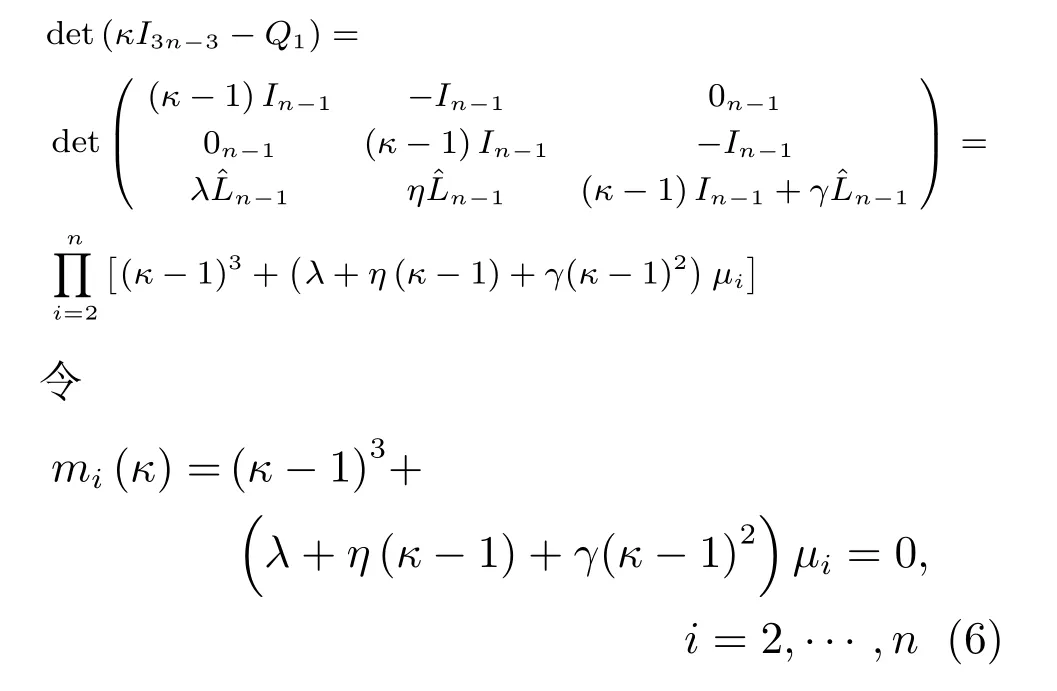
則有如下引理:

引理1[15].如果矩陣L有一個0特征值且其他所有特征值均有正實部,并且參數λ,η,γ滿足下列條件:

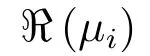
引理2[23].如果ρ(Q1)<1,那么存在M≥1和0<α<1使得下式成立

定理1.對于三階離散多智能體系統(1),基于假設1,如果式(2)中的耦合強度滿足引理1中的條件,觸發函數(4)中的參數滿足0<δ1<1,δ2>0,0<α<β<1,則稱系統(1)能夠實現漸近一致.

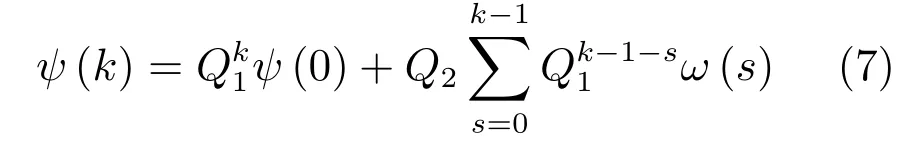
根據引理1和引理2可知,存在M≥1和0<α<1使得下式成立.

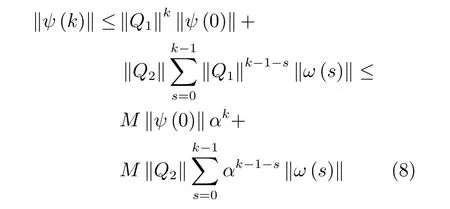
由觸發條件可得:

對上式移項可求解得:

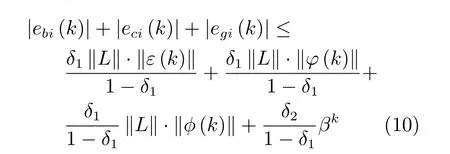
又因為kε(k)k≤kψ(k)k,k?(k)k≤kψ(k)k和kφ(k)k≤kψ(k)k,可得出下列不等式:

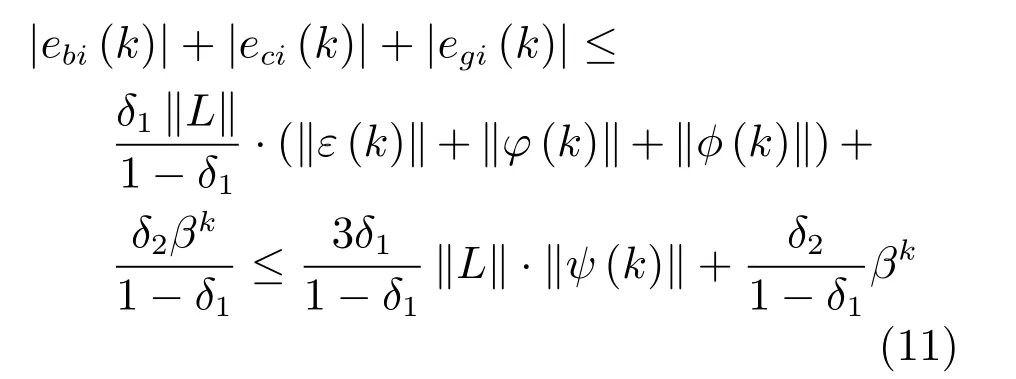
接著有如下不等式成立:

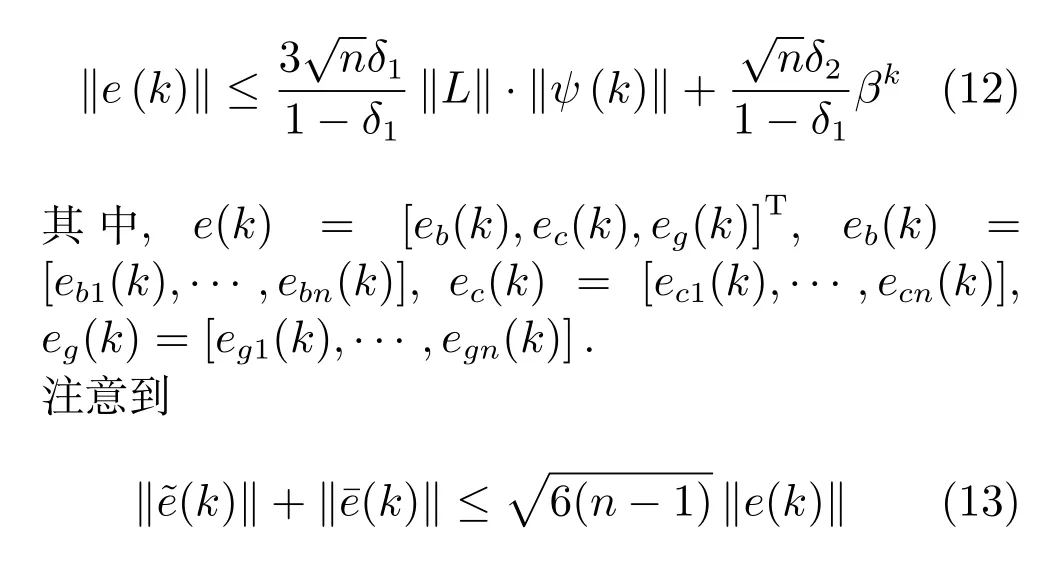
于是有

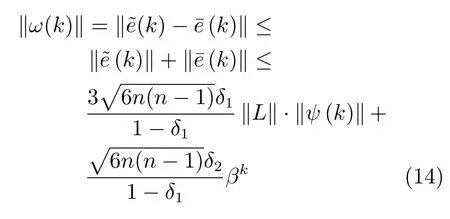
把式(14)代入式(8)可得

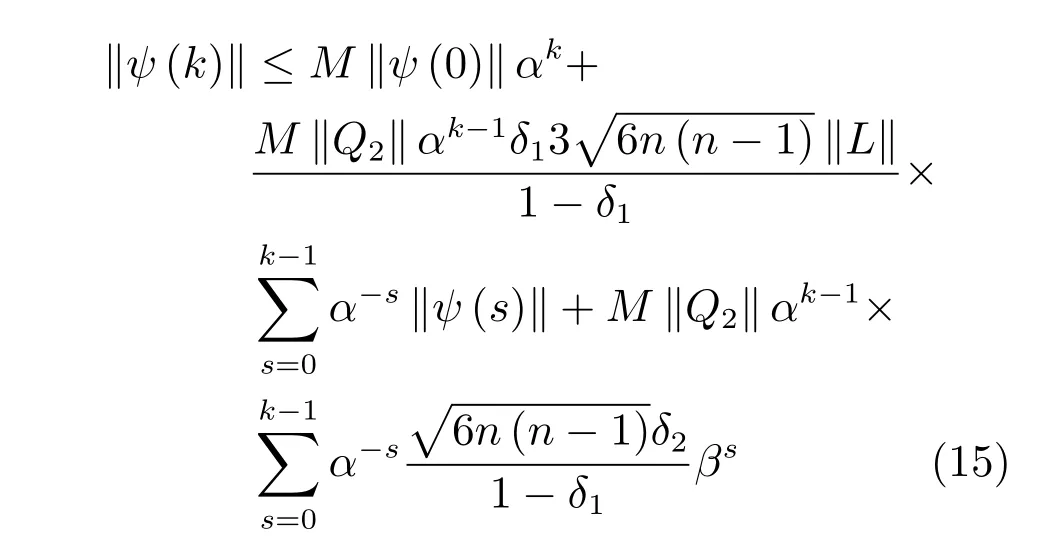
接下來的部分,將證明下列不等式成立.

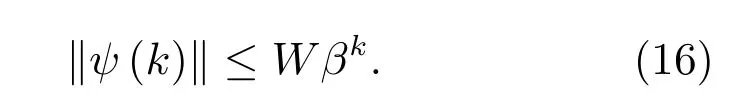
首先,證明對任意的ρ>1,下列不等式成立.

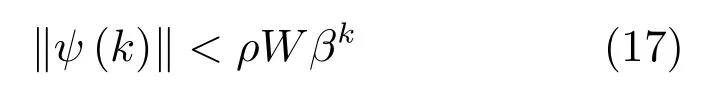
利用反證法,先假設式(17)不成立,則必將存在k?>0使得kψ(k)k≥ρWβk?并且當k∈(0,k?)時kψ(k)k<ρWβk成立.因此,根據式(17)可得:

根據以上結果,式(18)和式(19)都與假設相矛盾.這說明原命題成立,即對任意的ρ>1,式(17)成立.易知,如果ρ→1,則式(16)成立.根據式(16)可知,當k→+∞時,有limk→∞kψ(k)k=0,則系統(5)是收斂的.由ψ(k)的定義可知,系統(1)能夠實現漸近一致.

定理2.對于系統(1),如果定理1中的條件成立,并且控制器(2)中的設計參數滿足如下條件,

注2.類Zeno行為廣泛存在于基于事件觸發控制機制的離散系統中.然而,當前極少有文獻研究如何排除類Zeno行為,尤其是對于三階多智能體動態模型.定理2給出了排除三階離散多智能體系統的類Zeno行為的參數條件.

3 仿真實驗

本部分將利用一個仿真實驗來驗證本文所提算法及理論的正確性和有效性.假設三階離散多智能體系統(1)包含6個智能體,且有向加權通信拓撲結構如圖1所示,權重取值為0或1,可以明顯地看出該圖包含有向生成樹(滿足假設1).

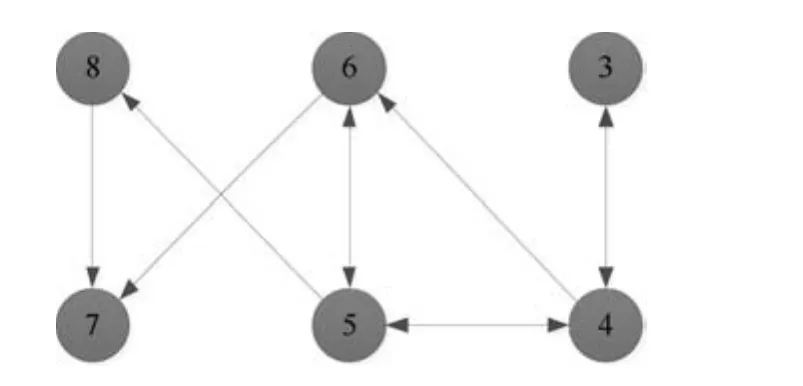
圖1 6個智能體通信拓撲結構圖Fig.1 The communication topology with six agents

通過簡單的計算可得,μ1=0,μ2=0.6852,μ3=1.5825+0.3865i,μ4=1.5825?0.3865i,μ5=3.2138,μ6=3.9360.令M=1,結合定理1和定理2可得到0.035<δ1<1,δ2>44.0025,0<α<β<1.令δ1=0.2,δ2=200,α=0.6,β=0.9,λ=0.02,η=0.3,γ=0.5,不難驗證滿足引理1的條件并且計算可知ρ(Q1)=0.9958<1.三階離散多智能體系統(1)的一致性結果如圖2～圖6所示.根據定理1可知,基于控制器(2)和事件觸發函數(4)的系統(1)能實現一致.從圖2～圖6可以看出,仿真結果與理論分析符合.

圖2 三階離散多智能體系統的位置軌跡圖Fig.2 The trajectories of position in third-order discrete-time multi-agent systems

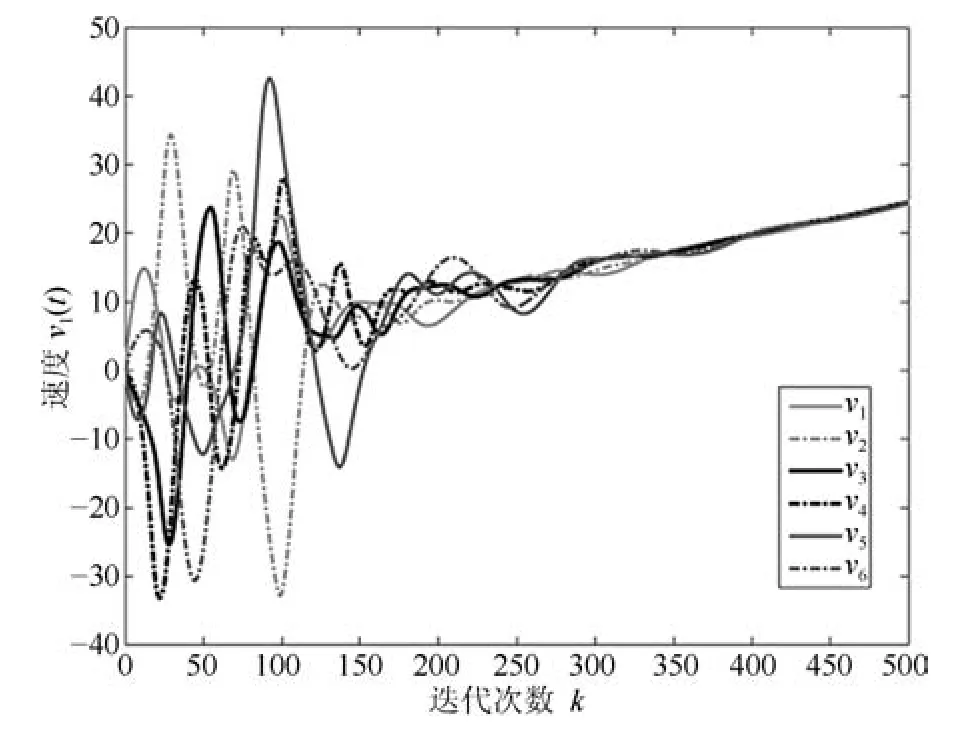
圖3 三階離散多智能體系統的速度軌跡圖Fig.3 The trajectories of speed in third-order discrete-time multi-agent systems

圖4 三階離散多智能體系統的加速度軌跡圖Fig.4 The trajectories of acceleration in third-order discrete-time multi-agent systems

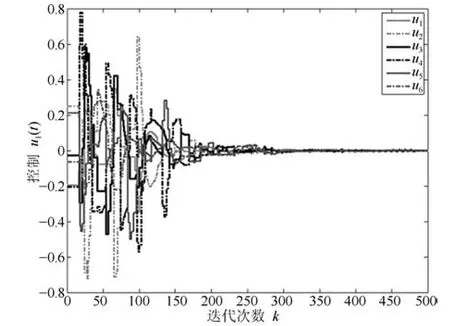
圖5 三階離散多智能體系統的控制軌跡圖Fig.5 The trajectories of control in third-order discrete-time multi-agent systems

圖6 100次迭代內所有智能體的觸發時刻Fig.6 Triggering instants of all agents within 100 iterations

圖2～圖4分別表征了系統(1)中所有智能體的位置、速度和加速度的軌跡,從圖中可以看出以上3個變量確實達到了一致.圖5展示了控制輸入的軌跡.為了更清楚地體現事件觸發機制的優點,圖6給出了0～100次迭代內的各智能體的觸發時刻軌跡.從圖6可以看出,本文設計的事件觸發協議確實達到了減少更新次數,節省資源的目的.

4 結論

針對三階離散多智能體系統的一致性問題,構造了一個新穎的事件觸發一致性協議,分析得到了在通信拓撲為有向加權圖且包含生成樹的條件下,系統中所有智能體的位置狀態、速度狀態和加速度狀態漸近收斂到一致狀態的充分條件.同時,該條件指出了通信拓撲的Laplacian矩陣特征值和系統的耦合強度對系統一致性的影響.另外,給出了排除類Zeno行為的參數條件.仿真實驗結果也驗證了上述結論的正確性.將文中獲得的結論擴展到拓撲結構隨時間變化的更高階多智能體網絡是極有意義的.這將是未來研究的一個具有挑戰性的課題.