延胡索熱風干燥特性及動力學行為

杜偉鋒， 顧 超， 康顯杰， 石森林， 李昌煜*， 葛衛紅*

（1. 浙江中醫藥大學， 浙江 杭州310053； 2. 浙江中醫藥大學中藥飲片有限公司， 浙江 杭州311401）

延胡索是罌粟科植物延胡索Corydalis yanhusuo W. T. Wang 的干燥塊莖[1], 為浙八味之一, 其主要成分包括延胡索乙素等生物堿類, 具有活血化瘀、 行氣止痛功效。 熱風干燥[2-3]是將空氣作為傳遞介質, 將熱量傳遞給物料, 水分吸收熱量擴散至表面, 由熱空氣帶走的過程, 廣泛應用于中藥飲片的生產加工。 熱風干燥技術成熟、 操作簡便、 受外界影響較小, 適用于中藥材產地加工。有學者對姜片[4]、 金銀花[5]、 茯苓[6]等干燥過程擬合, 研究干燥特性, 建立動力學模型。 本研究采用熱風干燥技術對延胡索鮮切片進行干燥, 通過研究溫度和裝載量對其干燥特性的影響, 建立延胡索干燥動力學模型, 為干燥工藝提供理論依據。

1 材料與方法

1.1 儀器 BWS-3-SN 電子天平（廈門佰倫斯電子科技有限公司, 精度±0.1 g）； DHZT-9070A 電熱恒溫鼓風干燥箱（上海精宏實驗設備有限公司）。

1.2 試藥 新鮮延胡索產自浙江磐安, 含水量（68.62 ± 0.25）%, 經浙江中醫藥大學中藥飲片有限公司質檢部錢敏主管中藥師鑒定為正品。

1.3 樣品制備 選擇干燥溫度（T,℃） 和裝載量（L, kg/m2） 作為變量, 其中裝載量為單位面積中供試品的質量。

稱取新鮮延胡索切片5 份, 厚度為4 mm, 分別稱取125.66、 188.50、 251.33、 314.16、 376.99 g,置于半徑為10 cm 的圓形托盤中, 使其裝載量分別為4、 6、 8、 10、 12 kg/m2, 分別置于鼓風干燥箱中熱風干燥, 溫度70 ℃, 風速恒定, 每隔20 min稱定質量, 直至含水量低于15%。

稱取新鮮延胡索切片5 份, 厚度為4 mm, 各稱取251.33 g, 置于半徑為10 cm 的圓形托盤中,使其裝載量為8 kg/m2, 分別置于鼓風干燥箱中熱風干燥, 溫度分別為50、 60、 70、 80、 90 ℃, 風速恒定, 每隔20 min 稱定質量, 直至含水量低于15%。

每組重復試驗3 次, 取平均值, 采用SPSS 19.0 軟件進行數據分析。

2 干燥模型及試驗指標

2.1 水分測定 按2015 年版《中國藥典》 “0832水分測定法” 中“第二法（烘干法） ” 測定[1]。

2.2 干基含水率 干基含水率[7-9]計算公式如下：

其中Wt為t 時刻延胡索的干基含水率, mt為t時刻延胡索的質量, mg為延胡索的干基質量, m0為延胡索的初始質量, W 為延胡索的初始濕基含水率。

2.3 干燥速率 干燥速率[10]計算公式如下：

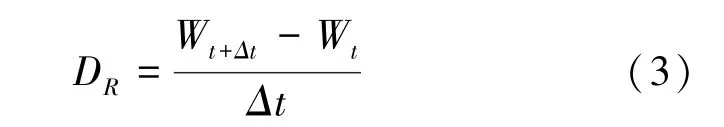
其中DR為干燥速率, Wt+Δt為t+Δt 時刻延胡索的干基含水率, Wt為t 時刻延胡索的干基含水率, Δt 為干燥間隔時間。

2.4 水分比（MR） 水分比（MR）[11]的簡化計算公式如下：

其中MR 為水分比, Wt為t 時刻延胡索的干基含水率, W1為初始時刻延胡索的干基含水率數據。

2.5 薄層干燥數學模型的選取 通過文獻調研,選取以下9 種常用的薄層干燥數學模型[7-10], 見表1, 該類模型適用于擬合物料質量降低只與水分蒸發相關的干燥過程。 本實驗的材料為新鮮延胡索切片, 揮發性成分較少, 屬于薄層干燥。

表1 常用薄層干燥數學模型Tab.1 Commonly drying mathematical model of thin layer

2.6 水分擴散系數的計算 在降速干燥階段, 干燥過程可用費克擴散方程對其描述, 方程適用于長方形、 圓形和球形等形狀的物料[12]。 假設所有的樣品都有相同的初始水分分布, 對于長時間的干燥過程, 其簡化方程表述如下[13]。

其中Deff為有效水分擴散系數（m2/s）, L0為樣品堆積厚度的一半（m）, 取對數可得, ln MR-t 呈線性關系, 通過計算斜率可得Deff。

2.7 干燥活化能 干燥活化能為1 mol 水分子發生有效碰撞時必須具備的相對平動能的最低值, 用于描述物料干燥的難易程度。 物料在干燥過程中,水分以擴散的形式離開物料表面[12]。 其擴散系數可用Arrhenius 公式表述[14], 可以來計算活化能Ea：

其中Do為指前因子, Ea為活化能（kJ/mol）,R 為摩爾氣體常量, 其數值為8.314×10-3kJ/（mol·K）,T為熱力學溫度（K）。 取對數可得, lnDeff-1/T 呈線性關系, 通過計算其斜率可得Ea。

3 結果

3.1 延胡索熱風干燥特性 不同熱風溫度下延胡索的干燥速率曲線、 水分比曲線見圖1～2； 不同裝載量下延胡索的干燥速率曲線、 水分比曲線見圖3～4。

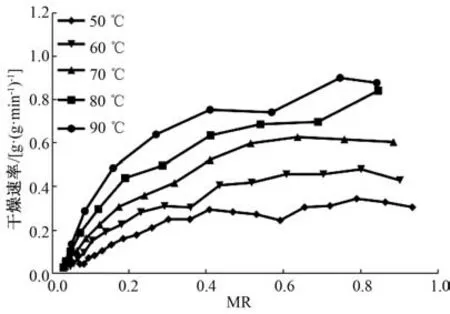
圖1 延胡索干燥速率曲線（I）Fig.1 Drying rate curves for Corydalis Rhizoma （I）

圖2 延胡索水分比曲線（I）Fig.2 Moisture ratio curves for Corydalis Rhizoma （I）

由圖1 可知, 在一定的溫度范圍內（50 ～90 ℃）, 延胡索熱風干燥過程由短暫的加速干燥階段后轉為降速干燥的階段, 初期干燥速率下降較慢, 后期干燥速度下降較快。 熱風溫度越高, 水分從表面蒸發的速度越快, 熱風溫度對延胡索的干燥速率影響顯著。

由圖2 可知, 隨著干燥時間的延長, 不同熱風溫度的延胡索水分比呈下降的趨勢。 初期水分比下降較快, 隨后下降速度變慢并逐漸趨于平緩。 熱風溫度在50～90 ℃范圍內, 溫度對水分比的影響顯著, 提高熱風溫度可以加速干燥過程, 可以大幅縮短干燥時間。

由圖3 可知, 裝載量10、 12 kg/m2的干燥速率曲線差異較小, 并有短暫的加速干燥階段后轉為降速干燥階段, 而4、 6、 8 kg/m2的干燥速率曲線只有降速干燥階段。 初期干燥速率下降較慢, 后期干燥速度下降較快。 裝載量越小, 水分從表面蒸發的速度越快, 所以干燥速率越大, 裝載量對延胡索的干燥速率影響顯著。

圖3 延胡索的干燥速率曲線（Ⅱ）Fig.3 Drying rate curves for Corydalis Rhizoma （Ⅱ）

圖4 延胡索的水分比曲線（Ⅱ）Fig.4 Moisture ratio curves for Corydalis Rhizoma （Ⅱ）

由圖4 可知, 水分比隨干燥時間延長不斷下降, 干燥初期水分比下降較快, 隨后下降速度變慢并逐漸趨于平緩。 裝載量4 ～12 kg/m2, 裝載量對水分比影響顯著, 降低裝載量可以加速干燥過程,大幅縮短干燥時間。

3.2 延胡索熱風干燥模型的建立 以裝載量8 kg/m2, 溫度70 ℃為例, 用所選的9 種薄層干燥模型, 對延胡索不同熱風干燥條件下的水分比曲線進行擬合, 得到各干燥模型的參數、 R2、 RMSE 和c2值, 結果見表2。

通過考察9 個模型的評價指標, 發現Page、Modified Page、 Modified Page equation-Ⅱ、 Modified Page 4 個模型的R2均大于0.999, RMSE 分別為0.007 165、 0.007 165、 0.007 165、 0.005 777, c2值分別為5.738×10-5、 5.738×10-5、 5.738×10-5、3.730×10-5, 表這4 個模型擬合程度均較高。 通過綜合比較, 選擇擬合曲線與實測值的差異較小, 模型評價指標R2值相對接近1, RMSE 和c2值較小,且模型參數較少的模型, 最終確定延胡索的熱風干燥采用Modified Page 模型進行擬合。

表2 不同薄層干燥模型參數Tab.2 Parameters of different thin layer drying models

3.3 模型求解 由表3 可知, Modified Page 模型中的干燥常數k 隨溫度的升高而增加, 而n 無規律性。 k 與物質的熱導性、 水分擴散性等干燥特性相關, 因此k 越大, 樣品的導熱效果越好, 干燥速率越快。

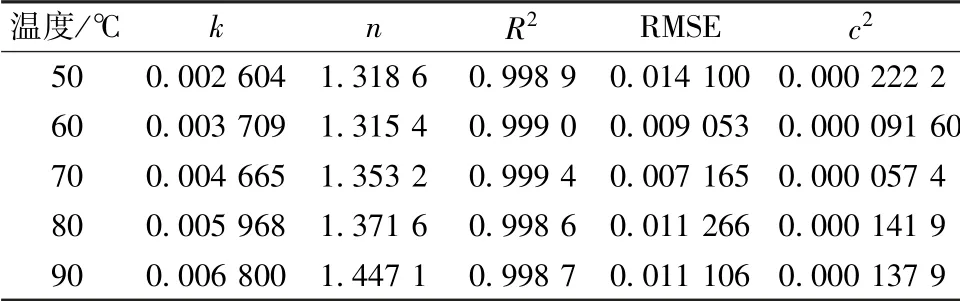
表3 Modified Page 模型干燥常數Tab.3 Drying constant of Modified Page

Modified Page 模型中的干燥常數k、 n 與延胡索的干燥溫度（T,℃） 和裝載量（L, kg/m2） 相關, 是關于溫度和裝載量的函數。 本研究采用二次多項式[5]擬合參數, 設定方程中的干燥常數n、 k的公式如下。

通過SPSS 軟件對數據進行擬合, 求解方程中待定參數, 剔除不顯著的影響因素（P＞0.05）, 得到n、 k 的回歸方程, 結果如下。

將以上各參數代入Modified Page 模型公式MR=exp [- （kt）n] 中, 得延胡索熱風干燥的模型方程。

3.4 Modified Page 模型驗證 為了驗證模型的擬合程度, 選取裝載量10 kg/m2、 干燥溫度80 ℃的干燥條件, 比較水分比實測值與模型的預測值, 結果見圖5。

圖5 實測值與預測值的差異Fig.5 Differences between measured and predicted values

由圖5 可知, 在裝載量10 kg/m2、 干燥溫度80 ℃的干燥條件下, 延胡索水分比的實測值與預測值差異較小, Modified Page 模型可用于延胡索的熱風干燥過程的預測。

3.5 有效水分擴散系數及活化能 由式（5） 可知, 延胡索飲片在干燥過程中, lnMR-t 呈線性關系[8], 通過對不同熱風溫度下lnMR-t 曲線的回歸計算, 得到對應的水分擴散系數Deff。 由表4 可知,干燥溫度在50 ～90 ℃時, 延胡索熱風干燥水分有效擴散系數范圍為3.972×10-10～1.362×10-9m2/s,水分有效擴散系數隨著溫度的升高而增大。

由公式（6） 可知, lnDeff-1/T 呈線性關系[9],根據擬合方程的斜率可以計算出延胡索熱風干燥的活化能Ea。 lnDeff-1/T 的線性回歸方程為lnDeff=-3 629 （1/T）-10.39, 則其活化能Ea為30.17 kJ/mol（R2=0.961 6）。

表4 延胡索水分有效擴散系數Tab.4 Effective moisture diffusion coefficient of Corydalis Rhizoma

4 討論與結論

在裝載量4 ～12 kg/m2, 50 ～90 ℃的條件下,Modified Page 模型對干燥過程的擬合度較好。 通過對模型參數的擬合, 確定參數與裝載量和溫度的函數關系, 建立的MR-t 函數, 能夠較為準確的預測不同溫度和裝載量下的水分比曲線, 通過比較干燥效率, 優化干燥工藝, 建立適合的延胡索產地加工方式； 并能預測不同時刻延胡索的水分比, 用于預測延胡索干燥至預定含水量所需的時間, 減少能耗, 提高產能。

在50 ～90 ℃范圍內, 延胡索熱風干燥主要是降速階段, 水分有效擴散系數隨著溫度的升高而增大, 范圍為3.972×10-10～1.362×10-9m2/s； Ea 為30.17 kJ/mol, 在20 ～40 kJ/mol 之間[15]。 因此在延胡索熱風干燥過程中, 除去的水分在固相骨架表面吸附的主要形式為物理吸附。