采用五棱鏡掃描法檢測大口徑平面鏡的面形

袁 理，張曉輝

(1.中國科學院 長春光學精密機械與物理研究所，吉林 長春 130033;2.中國科學院大學，北京 100049)

1 引 言

大口徑平面鏡通常是指口徑大于1 m的平面鏡。大口徑平面鏡在空間光學、天文光學等領域有著大量應用。為了確保大口徑平面鏡具有良好的質量，必須對其面形進行檢測。大口徑平面鏡面形的檢測方法主要有4種：直接干涉檢測法[1]、Ritchey-Common法[2-3]、子孔徑拼接法[4-7]和五棱鏡掃描法[8-15]。直接干涉檢測法需要一塊高精度的大口徑標準平面鏡，該鏡的加工難度很大，成本極高，因此該方法并不適用。Ritchey-Common法需要一塊高精度的大口徑標準球面鏡，成本也較高，并且由于光束是斜入射到平面鏡上的，所以光路搭建和調整也比較困難。子孔徑拼接法可以避免使用大口徑標準鏡，但是該方法的誤差累積現象比較嚴重，并且檢測時間較長，易受環境影響，所以檢測精度不是很高。五棱鏡掃描法通過測量表面傾斜角檢測大口徑平面鏡的面形，不需要使用大口徑標準鏡，成本較低，通過適當地設計算法和檢測流程，可以有效抑制各種主要誤差的影響，檢測精度較易保證，是一種比較好的方法，也是本文所研究的方法。

國內外研究人員提出了一系列不同的五棱鏡掃描法，大體上可分為兩種類型。第一種五棱鏡掃描法[8-12]是使用一個掃描的五棱鏡來直接測量表面傾斜角，這種方法受各種誤差的影響都較大，不宜采用。第二種類型的五棱鏡掃描法[13-15]是使用兩個五棱鏡來測量表面傾斜角的差值，其中一個是靜止的參考五棱鏡，另一個是運動的掃描五棱鏡；該方法可以消除傾斜誤差的一階影響和大部分環境的影響，但是由于兩個五棱鏡具有不同的制造誤差，所以五棱鏡制造誤差的影響不能在作差的過程中消除，因此該方法也有缺陷。另外，這兩種方法在掃描過程、算法等方面也各有一些不足。

針對上述問題，本文提出了一種新的五棱鏡掃描法，與以前的方法相比，主要有以下改進：第一，使用一個掃描的五棱鏡來測量表面傾斜角的差值，可以消除傾斜誤差的一階影響、五棱鏡制造誤差的影響和大部分環境的影響；第二，增加了一套反饋控制系統，用于自動監視和減小五棱鏡在掃描過程中的傾斜變化量；第三，對于兩個配對點，測量時間緊鄰著，而不是按照各點的排列順序依次測量，有利于減小環境變化的影響；第四，使用Zernike多項式來表示被測面形，然后建立超定方程組，通過最小二乘算法，直接得到二維面形，而不是先測出一維面形再進行拼接，不但減少了計算量，而且避免了拼接誤差。這些改進可顯著提高檢測的精度和效率。

2 檢測原理

2.1 表面傾斜角差值的測量

表面傾斜角測量原理圖如圖1所示。

圖1 表面傾斜角ε測量原理示意圖 Fig.1 Measurement schematic of the tilt angle ε of surface

如圖1所示，自準直儀發出的光束被五棱鏡偏轉90°后入射到平面鏡上，經平面鏡反射后再經過五棱鏡回到自準直儀，自準直儀可測出光束的偏轉角度φ，則平面鏡在掃描方向上的表面傾斜角ε等于：

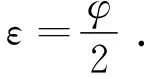
(1)

五棱鏡具有優良的誤差抑制特性，五棱鏡的傾斜誤差對ε的測量值僅產生很小的二階影響[16]。然而，自準直儀的傾斜誤差、被測平面鏡的整體傾斜誤差、五棱鏡的制造誤差以及環境帶來的誤差卻對ε的測量值影響很大，但是，如果將兩個點處的ε值作差，則可以有效抑制這些誤差的影響。在五棱鏡掃描過程中，設自準直儀在兩個點處的讀數分別為φ1和φ2，測得的表面傾斜角分別為ε1和ε2，則這兩個點的表面傾斜角的差值δ等于：

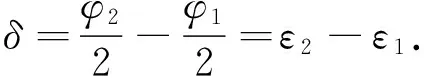
(2)

圖2為自準直儀存在傾斜角ω時的測量示意圖。

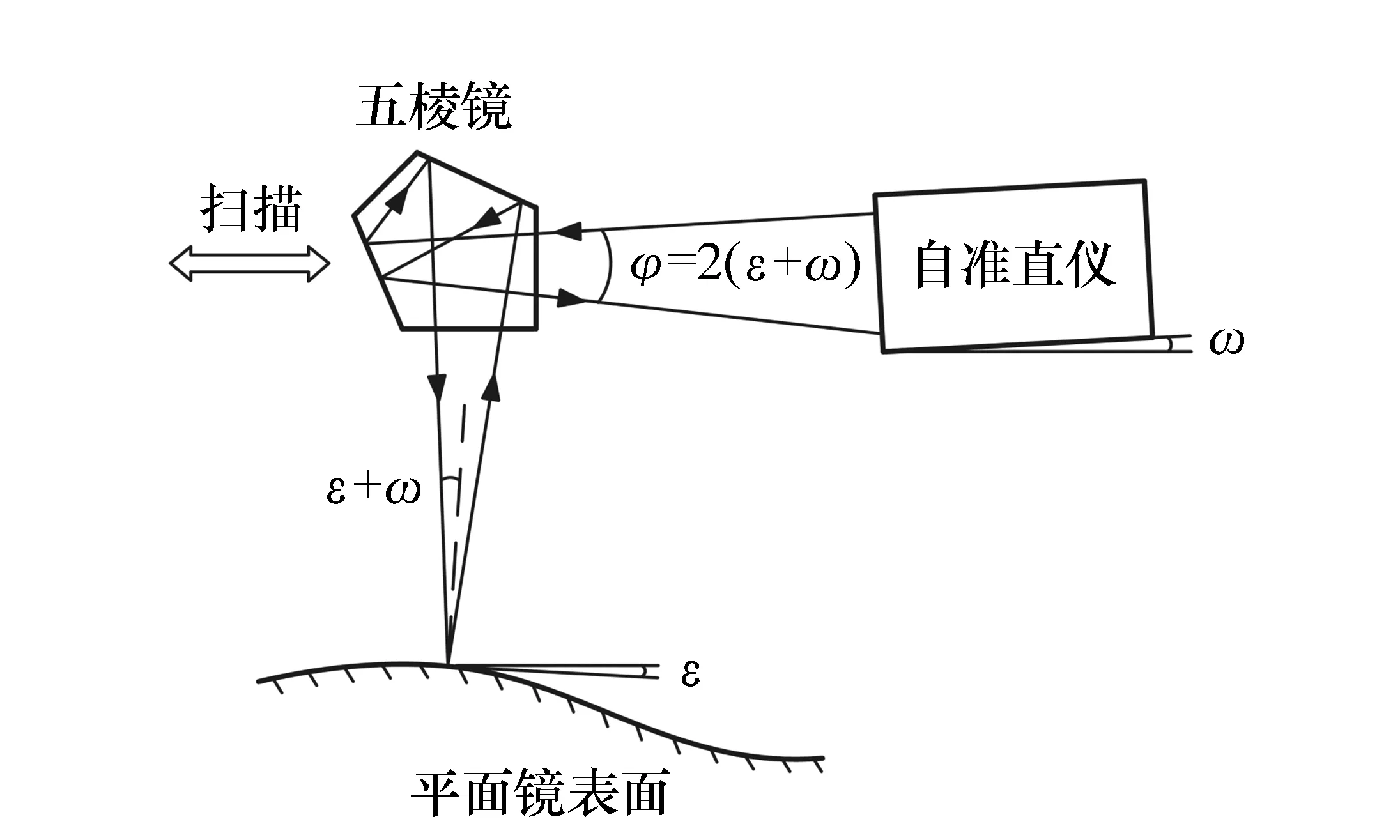
圖2 自準直儀存在傾斜角ω時測量示意圖 Fig.2 Measurement schematic when autocollimator has a tilt angle ω

如圖2所示，如果自準直儀存在ω角的傾斜誤差，則自準直儀在這兩個點處的讀數φ1和φ2變為：

φ1=2(ε1+ω),φ2=2(ε2+ω) .

(3)

在五棱鏡掃描過程中，自準直儀是不動的，所以ω角不變，于是得到表面傾斜角的差值δ等于：

(ε1+ω)=ε2-ε1.

(4)

可見，式(4)與式(2)的結果是相同的，自準直儀的傾斜誤差ω在作差的過程中抵消掉了，從而對δ不產生影響。類似地，被測平面鏡的整體傾斜誤差、五棱鏡的制造誤差以及大部分環境帶來的誤差也在作差的過程中抵消，詳見第4節的誤差分析。

2.2 掃描方式

首先定義兩種距離d和D。將作差的兩個點稱為“配對點”。如圖3所示，假設在某一條掃描直線上有6個測量點，其中第1點和第4點配對作差，第2點和第5點配對作差，第3點和第6點配對作差，則將d稱為“兩個配對點的距離”，將D稱為“點對的距離”。D實際上就是采樣間距。

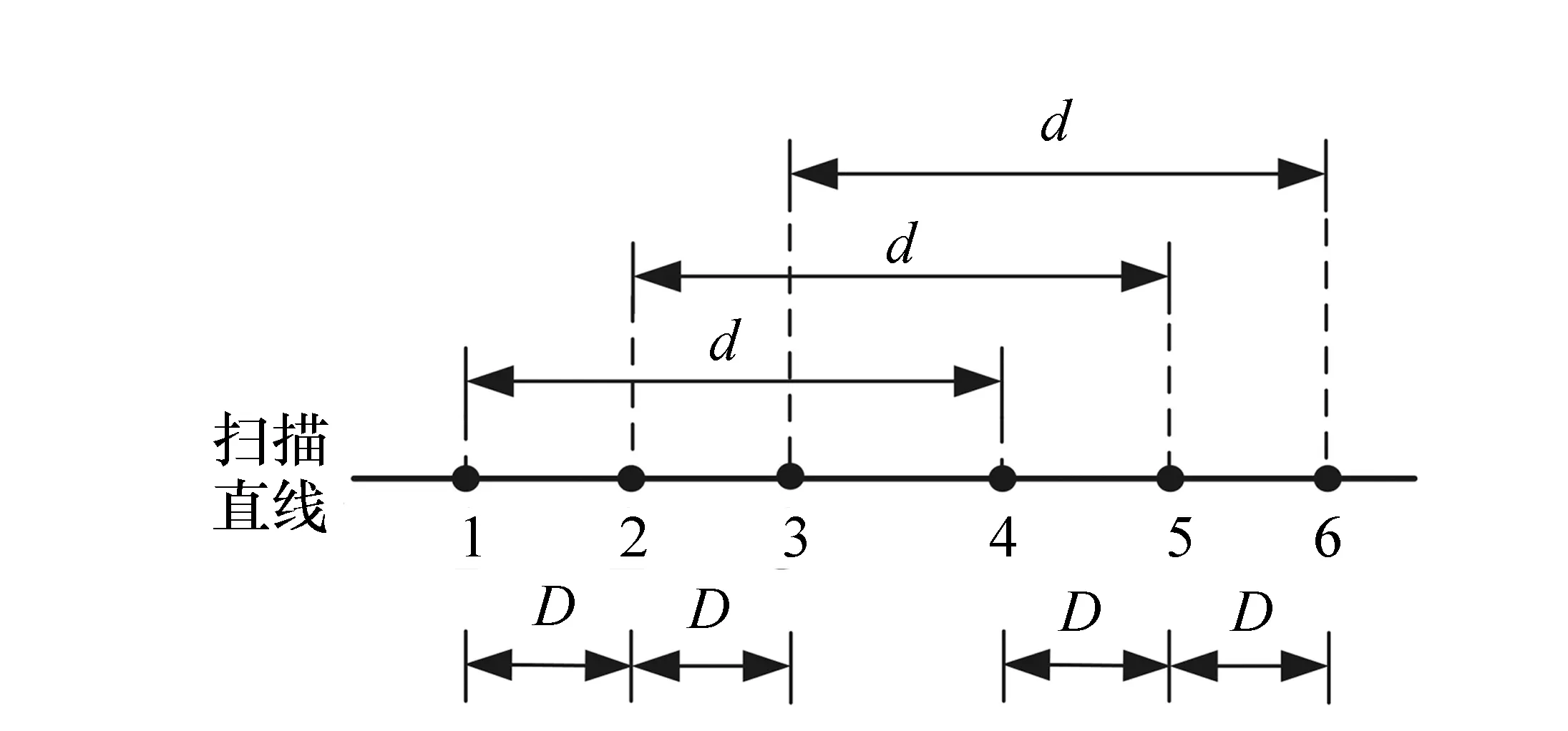
圖3 距離d和D的定義 Fig.3 Definitions of the distances d and D

需要注意的是，對兩個配對點的測量有一段時間間隔，如果在這段時間間隔里環境發生了變化，那么在作差時，環境的影響就不能完全抵消。所以，要盡量減小兩個配對點測量時間的間隔，以減小環境變化的影響。因此需要做到以下兩點：第一，對兩個配對點的測量必須在時間上緊鄰著，例如，如圖3所示，測量的順序應該是1、4、2、5、3、6，而不能是1、2、3、4、5、6；第二，五棱鏡的運動速度要盡量快，距離d不能太大，以減少五棱鏡在兩個配對點之間的運動時間。另外，距離d也不能太小，如果d太小，則表面傾斜角的差值δ就會很小，在絕對誤差不變的情況下，相對誤差就會很大。在充分考慮這些因素后，在本文的實驗中，d取150 mm，五棱鏡的運動速度為20 mm/s，運動時間為7.5 s。

掃描路徑如圖4所示，采用極坐標掃描路徑，共掃描20條直線，所有掃描直線交匯于被測平面鏡中心。相鄰掃描直線之間的夾角為π/20，而被測平面鏡的直徑為1.5 m，因此其邊緣的采樣間距等于750 mm×π/20≈120 mm，在被測平面鏡的中心，采樣間距接近于0，所以平均采樣間距為120 mm/2=60 mm，相應地，點對的距離D也取60 mm。這樣，每條半徑上測量11對配對點，共測量440對配對點。另外，采樣口徑取27 mm。

圖4 掃描路徑 Fig.4 Scanning paths

2.3 被測平面鏡面形的計算

在柱坐標系下，將被測平面鏡的面形S(ρ,θ)表示為Zernike多項式Zi(ρ,θ)[17]的線性組合如下：

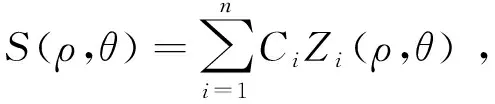
(5)

其中：n為Zernike多項式的項數，在本文中n取36；Ci為各項Zernike多項式的系數。由于Zernike多項式是定義在單位圓上的，所以有0≤ρ≤1。

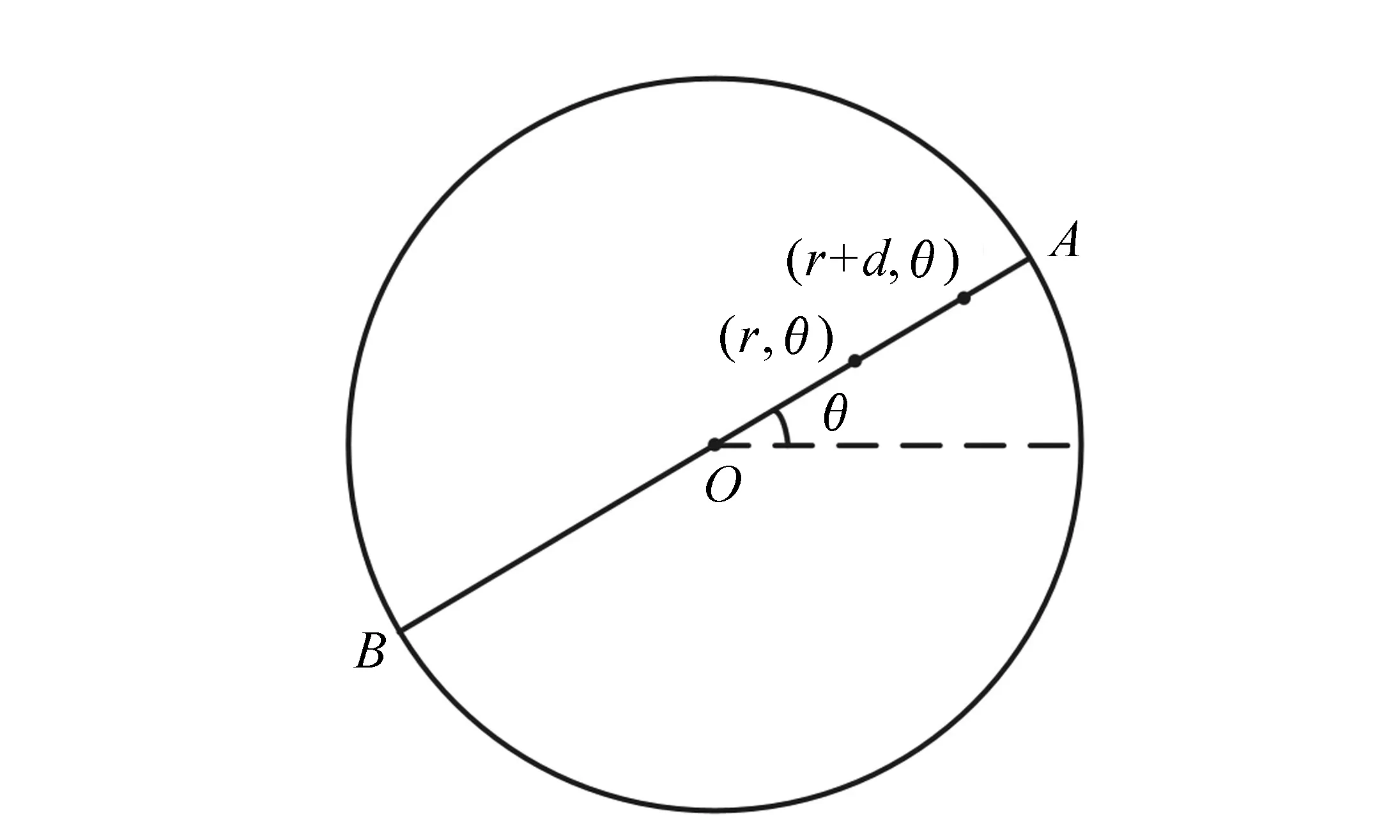
圖5 兩個配對點的極坐標 Fig.5 Polar coordinates of two matching points

設某一條掃描直線AOB上有兩個配對點，它們到中心O的距離分別為r和r+d，極坐標分別為(r,θ)和(r+d,θ)，如圖5所示。將它們的極徑歸一化為ρ1和ρ2：

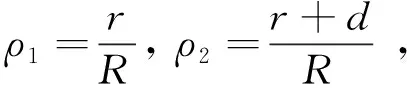
(6)

其中：R是被測平面鏡的半徑。設這兩個配對點的表面傾斜角為ε1和ε2，由于ε1和ε2是沿徑向方向的，并且都比較小，所以得到：

(7)

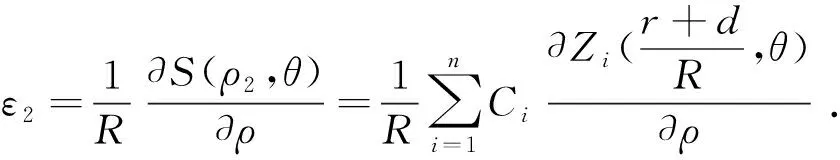
(8)

由于作了極徑的歸一化，使得被測平面鏡的半徑從R縮小為1，這樣，各點的斜率實際上就變為了原來的R倍，因此需要在式(7)和式(8)的右端乘以1/R。將(8)式和(7)式相減，得到表面傾斜角的差值δ等于：

(9)

在式(9)中，只有Ci是未知的。每測量一對配對點，都可以根據式(9)得到一個關于Ci的方程，在測量完所有配對點后，就可以得到關于Ci的超定方程組，然后通過最小二乘法就可以求出Ci，再根據式(5)就可以得到被測平面鏡的面形表達式。

在檢測過程中，還需要注意以下兩點：第一，在同一條掃描直線上，在中心O的兩側，表面傾斜角的正方向是相反的；第二，兩個作差的配對點必須位于同一條掃描直線上，并且位于中心O的同一側，即它們必須具有相同的極角θ，只有這樣才能在作差時抵消掉所有的一階傾斜誤差。

2.4 五棱鏡傾斜變化量的自動監視與調整

為了監視五棱鏡在掃描過程中的傾斜變化量，在檢測系統中增加了一個自準直儀和一個返回平面鏡。如圖6所示，自準直儀1與五棱鏡用于測量表面傾斜角，增加的自準直儀2與返回平面鏡用于監視五棱鏡的傾斜變化量。五棱鏡和返回平面鏡安裝在同一個底座上。

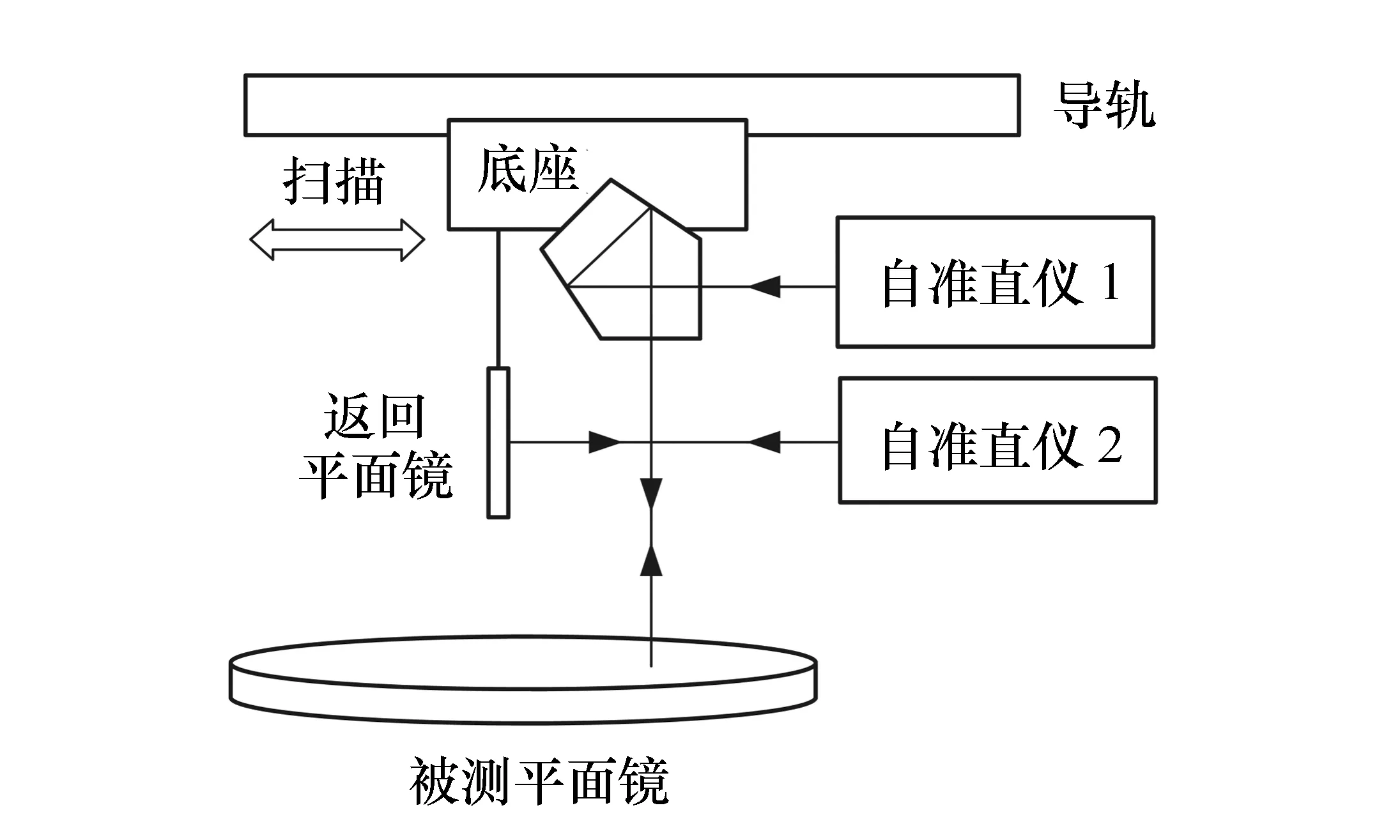
圖6 自準直儀2和返回平面鏡監視五棱鏡的傾斜變化量示意圖 Fig.6 Schematic of using autocollimator 2 and the return mirror to monitor the changes of pentaprism tilts

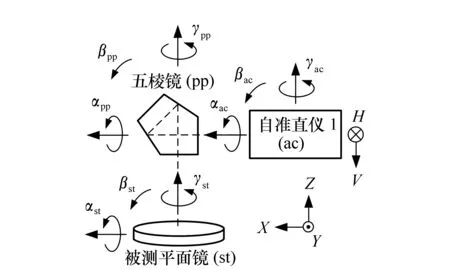
圖7 各個光學組件的傾斜角 Fig.7 Tilt angles of the optical components

圖7畫出了各個光學組件的傾斜誤差角，α、β和γ分別表示繞X軸、Y軸和Z軸的傾斜誤差角，下標ac、pp和st分別表示自準直儀1、五棱鏡和被測平面鏡。注意，βst由兩部分組成，一是被測平面鏡的整體傾斜，二是被測平面鏡局部的表面傾斜，αst也一樣。

V和H分別表示自準直儀1在兩個方向上的讀數值的一半，V實際上就等于式(1)中的ε加上一些誤差項。通過光路追跡，可以得到V和H等于[18]：

αst(αpp+γpp)-βst+βac+V0，

(10)

H=βst(αpp+γpp-γst-αac)+

αst-αpp+γpp-γac+H0.

(11)

在以上兩式中，角度的單位必須是弧度，典型的換算關系為1 μrad等于0.2″。V0和H0是兩個常量，來源于五棱鏡的制造誤差。現在用Δ來表示相對于掃描前的變化量。忽略式(11)中很小的二階項，得到H的變化量ΔH等于：

ΔH=Δαst-Δαpp+Δγpp-Δγac+ΔH0.

(12)

在五棱鏡掃描過程中，自準直儀1是不動的，所以Δγac=0；H0是一個常量，所以ΔH0=0；對于拋光后的平面鏡，Δαst大致在3 μrad rms左右，而在本系統中，五棱鏡在掃描過程中的傾斜變化量Δαpp和Δγpp大致在60 μrad rms左右。可見Δαst遠小于Δαpp和Δγpp，所以忽略(12)式中的Δαst，得到：

Δαpp=Δγpp-ΔH,

(13)

其中，Δγpp可由自準直儀2測得，ΔH可由自準直儀1測得，于是根據式(13)即可求出Δαpp。獲得Δγpp和Δαpp的值后，就可以通過反饋控制和自動調整來減小它們。一般可以將Δγpp和Δαpp減小到15 μrad rms以內，實際上就減小了傾斜誤差的二階影響。

注意，Δβpp對檢測無影響，因此無需對它進行監視與調整；另外，在每個測量點處，必須在測量表面傾斜角以前完成監視與調整。

2.5 檢測原理的仿真分析

為了驗證檢測原理的正確性，按照2.2節中所述的參數，對檢測原理進行了仿真分析，計算軟件采用MATLAB。仿真分析步驟如下：第一步，假設出任意36個Zernike多項式系數的真值，得到被測平面鏡的真值面形；第二步，利用Zernike多項式系數的真值，按照式(9)計算出440個表面傾角差值的真值，然后利用這些表面傾角差值的真值，按照2.3節的方法計算出Zernike多項式系數的仿真值，得到仿真面形；第三步，將仿真面形與真值面形作差，得到面形復原誤差，再計算該面形復原誤差的rms值。

按以上步驟重復計算10次，得到10個rms值，它們的最大值僅為2.3 nm rms，可見檢測原理是正確的，原理誤差為2.3 nm rms。

3 檢測系統

圖8 檢測系統 Fig.8 Measurement system

檢測系統如圖8所示。五棱鏡和返回平面鏡安裝在同一個底座上，底座上有傾斜自動調整機構。底座可在兩根長度為2.2 m的掃描導軌上滑動，采用兩根導軌可以減小掃描過程中的傾斜。五棱鏡的位置由光柵尺測出，光柵尺的測量精度為0.005 mm rms。兩個自準直儀安裝在導軌的一端，型號均為SH-LTP，由法國Imagine Optic 公司生產，光束口徑為27 mm，波長為405 nm，測量精度為100 nrad rms，測量范圍為±12 mrad。上述部件都安裝在旋轉臂上，旋轉臂連接于轉臺上，通過旋轉來實現多條徑向直線的掃描。轉臺可以輸出旋轉臂的角度位置，轉臺的轉角精度為75 μrad rms。當旋轉臂旋轉時，它的傾斜變化量為70 μrad rms。轉臺可以在兩根水平導軌上滑動，以實現與被測平面鏡的對準。該檢測系統可以檢測口徑不大于2.1 m的平面鏡的面形。

采用Geckeler介紹的方法[18]對檢測系統進行初始調整，初始調整是以自準直儀1為基準的。通過初始調整，可以使所有光學元件的初始傾斜誤差均在10 μrad rms以內。

4 誤差分析

4.1 傾斜誤差

設P1和P2為兩個作差的配對點，Δ表示參數從P1到P2的變化量。注意，這里的Δ與2.4節中的Δ的含義不同。利用誤差傳遞公式[19]，通過求偏導數，由式(10)可以得到V從P1到P2的變化量ΔV等于：

ΔV=Δαpp(-2αpp+αac+αst)+

Δγpp(-αac+αst)+

Δαac(αpp-γpp-αst)+

Δαst(-αac+αpp+γpp)-

Δβst+Δβac+ΔV0.

(14)

ΔV實際上就等于式(2)中的δ加上一些誤差項。由于自準直儀1是不動的，因此Δαac=Δβac=0；V0是常量，因此ΔV0=0；被測平面鏡是不動的，因此βst中的整體傾斜部分沒有變化，所以(-Δβst)實際上就是表面傾斜角的差值δ，于是δ的誤差Eδ等于：

Eδ=Δαpp(-2αpp+αac+αst)+

Δγpp(-αac+αst)+

Δαst(-αac+αpp+γpp) .

(15)

從式(15)可以看出，通過計算表面傾斜角的差值，使V中的所有一階誤差項全部消除，只剩下很小的二階誤差項。表1列出了一些傾斜誤差角的值，這些值來源于2.4節和3節，其中變化量

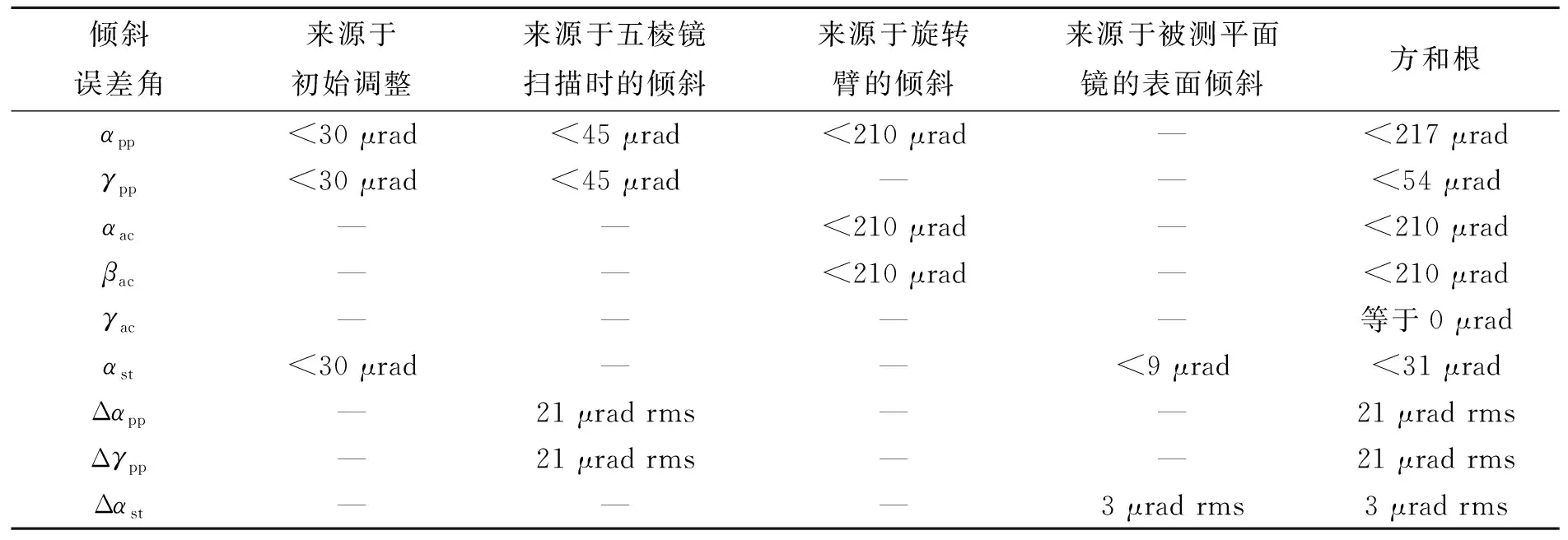
表1 各個傾斜誤差角的值Tab.1 Values of tilt angle error

Δαpp，Δγpp和Δαst的值使用rms誤差，而其它傾斜誤差角的值使用極限誤差。在本文中，極限誤差等于相應的rms誤差的3倍。對于表1，需要注意兩點：第一，αac、βac和γac中不含有初始調整誤差，因為在初始調整過程中，自準直儀1是基準；第二，γpp和γac中不含有旋轉臂的傾斜誤差，因為旋轉臂的γ傾斜角誤差實際上是轉臺的轉角誤差，這將在后面的4.3節中進行分析。

表2和表3對Eδ的值進行了計算。注意，在誤差分析時，需要將式(15)中的所有負號變為正號；另外，在表3中，將極限誤差值看作常數。最后得到由傾斜誤差造成的表面傾斜角差值δ的誤差Eδ等于11.1 nrad rms。

表2 計算式(15)的一些組成部分Tab.2 Calculations of some components in Equation (15)(μrad)

表3 計算Eδ的值Tab.3 Calculations of Eδ

4.2 自準直儀1的測量誤差

自準直儀1的測量誤差為100 nrad rms，根據式(2)，可得到相應的表面傾斜角差值δ的誤差為：

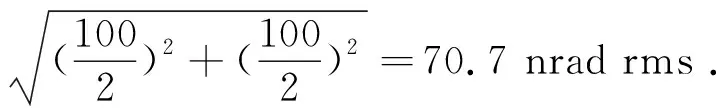
(16)

4.3 測量點的位置誤差

轉臺的轉角誤差為75 μrad rms，如果被測平面鏡的半徑為750 mm，則相應測量點的最大位置誤差等于：

75×10-6×750=0.056 mm rms .

(17)

光柵尺的測量誤差為0.005 mm rms，由此帶來的測量點的位置誤差也為0.005 mm rms。

在式(10)和式(11)中，除了αst和βst以外的一階項αpp、γpp、βac、γac、V0和H0，均會使射向被測平面鏡的光束產生傾斜，傾斜角的大小分別等于αpp、γpp、βac、γac、V0和H0本身的大小。這種光束的傾斜會帶來測量點的位置誤差，如表4所示，最后計算得到相應測量點的位置誤差為0.052 mm rms。表4中αpp、γpp、βac和γac的值來源于表1，V0和H0的值通過實驗標定。

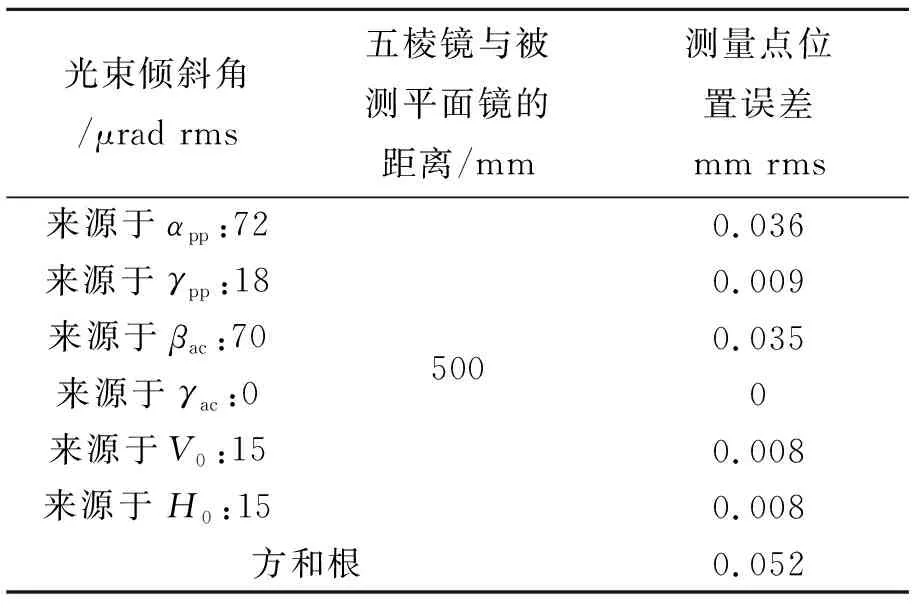
表4 計算光束傾斜帶來的測量點位置誤差Tab.4 Calculations of the position errors caused by beam tilts

將以上3種來源的測量點位置誤差進行合成，得到測量點的總位置誤差：

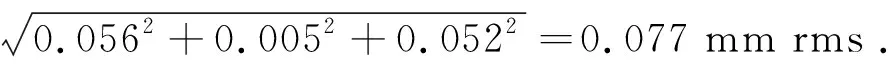
(18)

被測平面鏡的表面起伏一般是很平緩的，其表面傾角的變化一般不大于15 nrad/mm。0.077 mm rms的位置誤差對應的表面傾斜角的誤差等于1.2 nrad rms，于是根據式(2)，相應的表面傾斜角差值δ的誤差等于1.7 nrad rms。

4.4 五棱鏡的制造誤差

五棱鏡的制造誤差會使出射光產生固定的偏角V0和H0[18]，在4.1節、4.3節中已經對V0和H0進行了分析。 由式(15)可知，V0在作差的過程中已抵消。

4.5 環境變化帶來的誤差

為了減小環境變化的影響，整個檢測系統和被測平面鏡放置在同一個隔振平臺上，環境溫度控制為(20±0.2) ℃。在檢測過程中，停止人員的走動和其它無關儀器的工作，以盡量減少振動和空氣擾動。

如2.2節所述，五棱鏡在兩個配對點之間的運動時間為7.5 s，再加上五棱鏡傾斜變化量的監視與調整所需的時間，測量兩個配對點的時間間隔在10 s左右，在這段很短的時間內，環境的變化量很小，因此環境的影響在作差時幾乎可忽略。

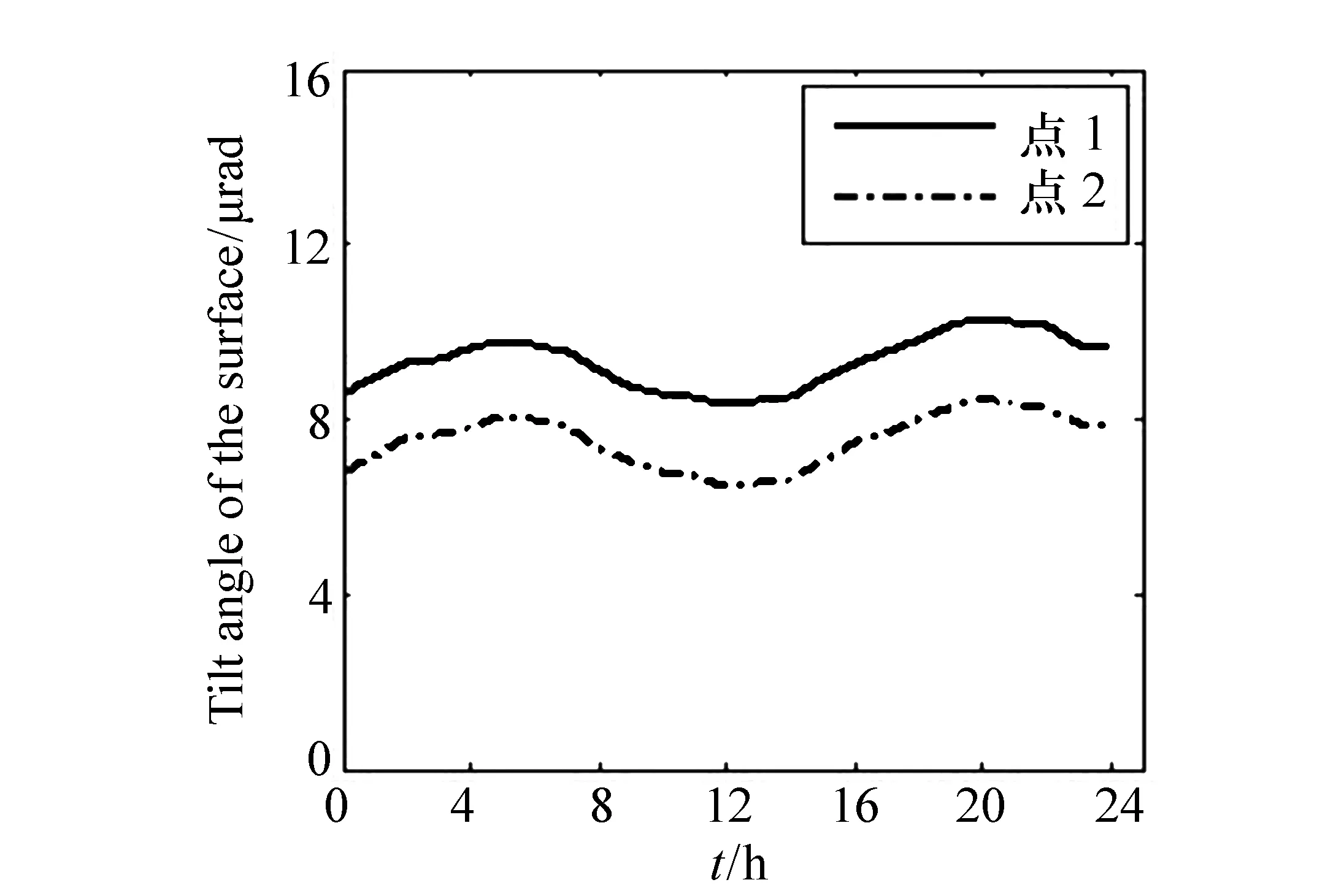
圖9 表面傾角的測量結果 Fig.9 Results of the tilt angles of surface

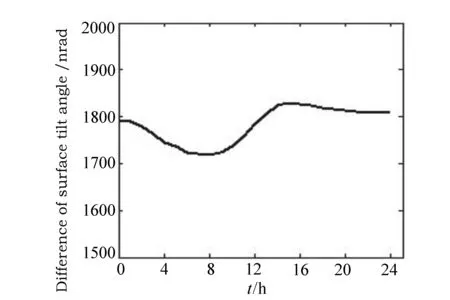
圖10 表面傾角差值的測量結果 Fig.10 Results of the surface tilt angle difference

下面通過實驗來測量環境變化的誤差。在被測平面鏡上選擇了相距150 mm的兩個配對點，分別記為點1和點2，對這兩個點的表面傾斜角的差值進行測量，每10 min測量一次，共測量24 h。表面傾角的測量結果如圖9所示，表面傾角差值的測量結果如圖10所示。從圖9可以看出，這兩個點的表面傾角的變化趨勢是一樣的，變化量也幾乎相同，因此變化量在作差時可以抵消；從圖10可以看出，表面傾角差值的變化量很小。最后計算得到，點1的表面傾角的標準偏差為607.6 nrad，點2的表面傾角的標準偏差為620.2 nrad，表面傾角差值的標準偏差為38.5 nrad。

4.6 表面傾角差值δ的誤差匯總

綜上，表面傾角差值δ的誤差匯總見表5，其總誤差為81.3 nrad rms。

表5 表面傾角差值的誤差匯總Tab.5 The combined error of the surface tilt angle difference

4.7 仿真分析確定面形檢測精度

通過前面的分析得到，表面傾角差值δ的測量誤差為81.3 nrad rms，在此基礎上，通過仿真分析確定由δ的誤差造成的面形檢測誤差。

按照2.2節中所述的參數進行仿真分析，計算軟件采用MATLAB。仿真分析步驟為：第一步，已知對于拋光后的平面鏡，其上任意兩點的表面傾角的差值大致為3 μrad rms左右，其隨機產生440個3 μrad rms的表面傾角差值，分別與440對配對點相對應，然后利用這些表面傾角差值，按2.3節的方法計算出面形，記為面形1；第二步，隨機產生440個81.3 nrad rms的誤差值，把這些誤差值分別加到440個表面傾角差值上，得到含有誤差的440個表面傾角差值，再利用它們來計算出含有誤差的面形，記為面形2；第三步，將面形2與面形1作差，得到面形檢測誤差，再計算該面形檢測誤差的rms值。

按以上步驟重復計算10次，得到10個rms值，它們的最大值為7.2 nm rms，即為由δ的誤差造成的面形檢測誤差。

在2.5節中，已經通過仿真分析得到了檢測的原理誤差，為2.3 nm rms，于是總的面形檢測誤差等于：

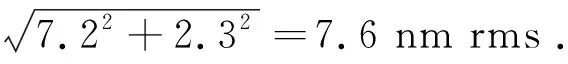
(19)

所以五棱鏡掃描法的面形檢測精度為7.6 nm rms。

5 檢測實驗與結果對比

采用圖8所示的檢測系統對一塊口徑為1.5 m的平面鏡的面形進行了檢測實驗，如圖11所示，檢測原理與檢測參數如第2節所述。

圖11 檢測1.5 m口徑平面鏡的面形 Fig.11 Surface shape detection of a 1.5 m flat mirror

對面形共檢測了5次，5次檢測的平均面形如圖12所示。5次檢測的標準偏差如圖13所示，最大標準偏差為6.1 nm，僅出現在平面鏡邊緣，平均標準偏差為4.0 nm，可見，檢測重復性較好。

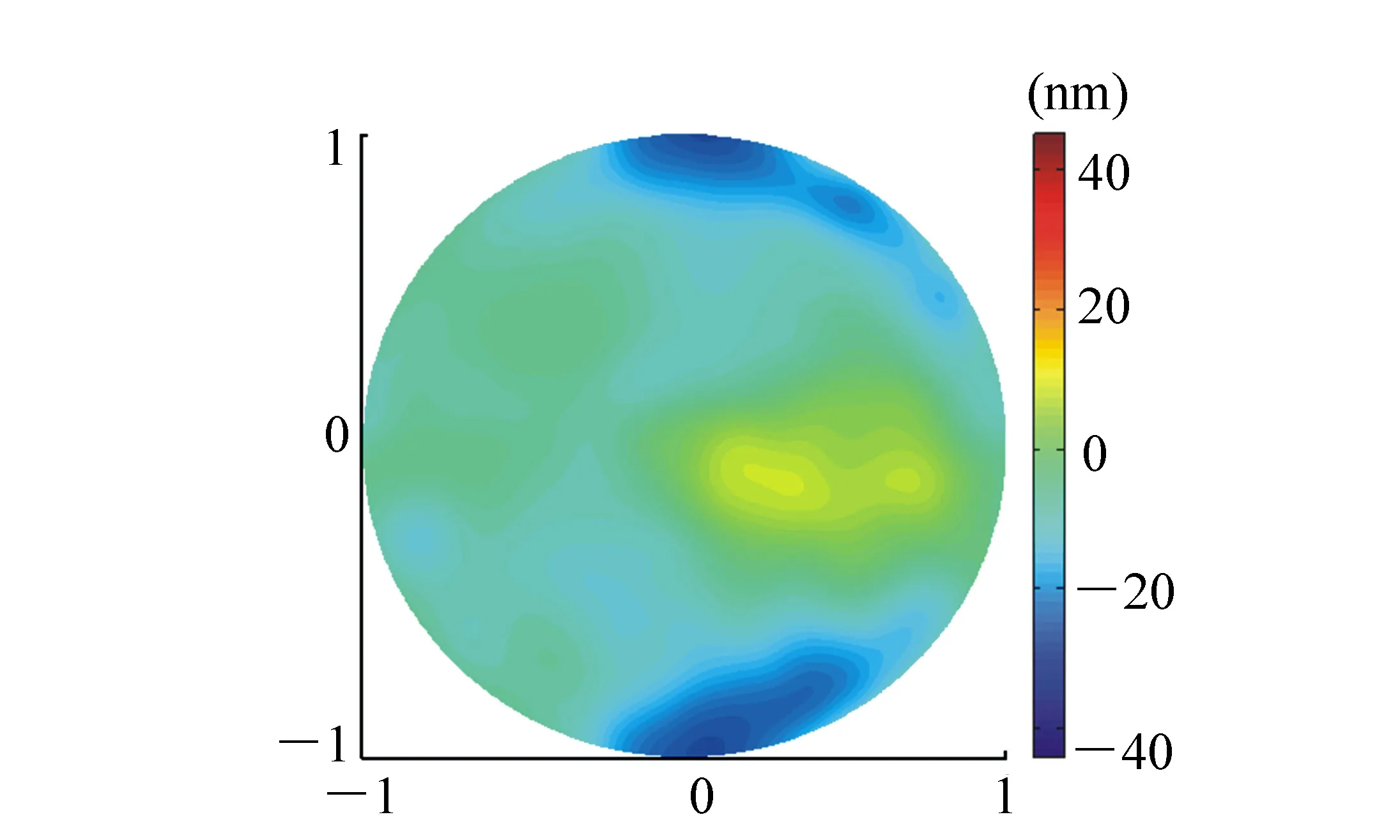
圖12 5次檢測的平均面形(PV=45.3 nm，RMS=13.2 nm) Fig.12 Average surface shape of 5 times of measurements(PV=45.3 nm，RMS=13.2 nm)

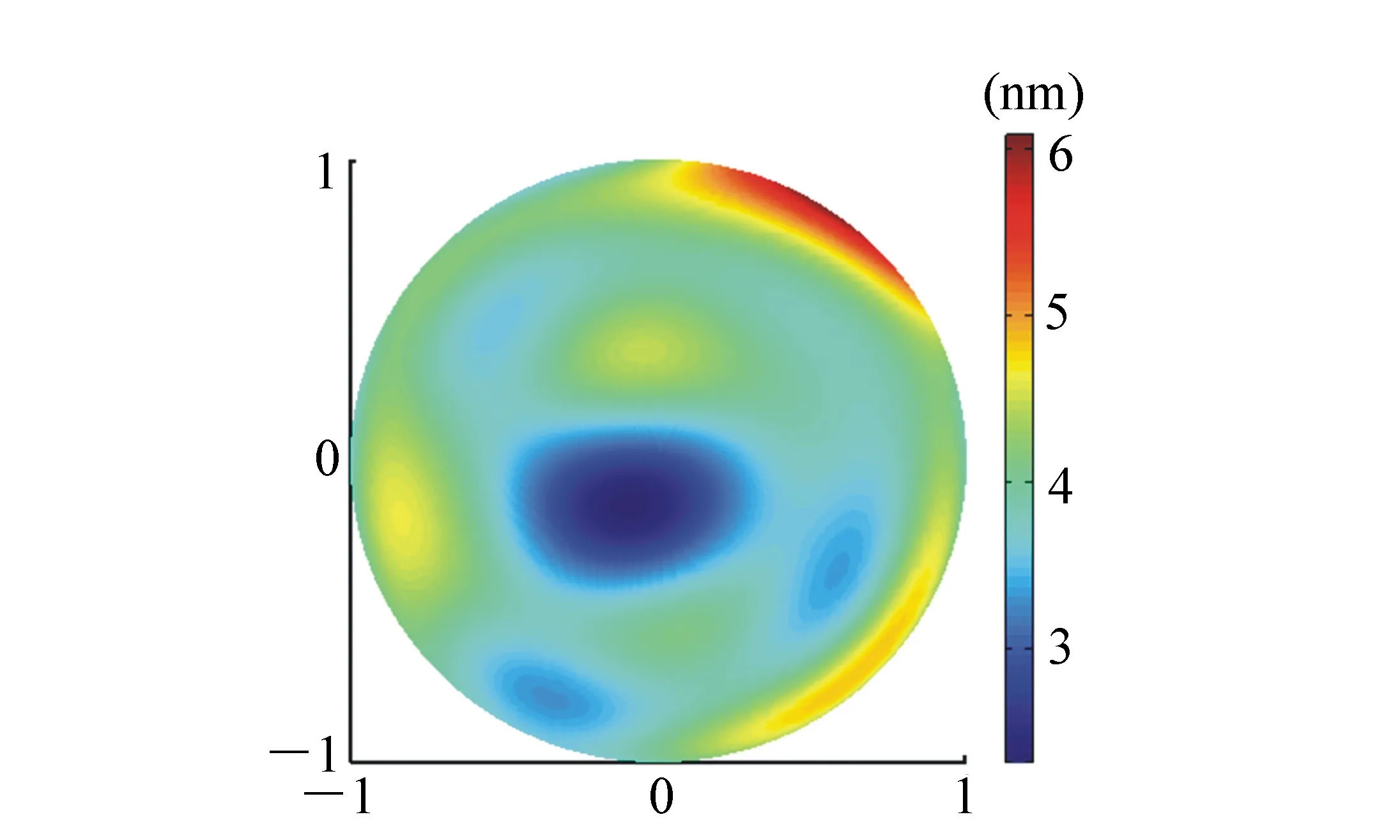
圖13 5次檢測的標準偏差 Fig.13 Standard deviation of 5 times of measurements

圖14 Ritchey-Common法的檢測光路 Fig.14 Light path of Ritchey-Common method

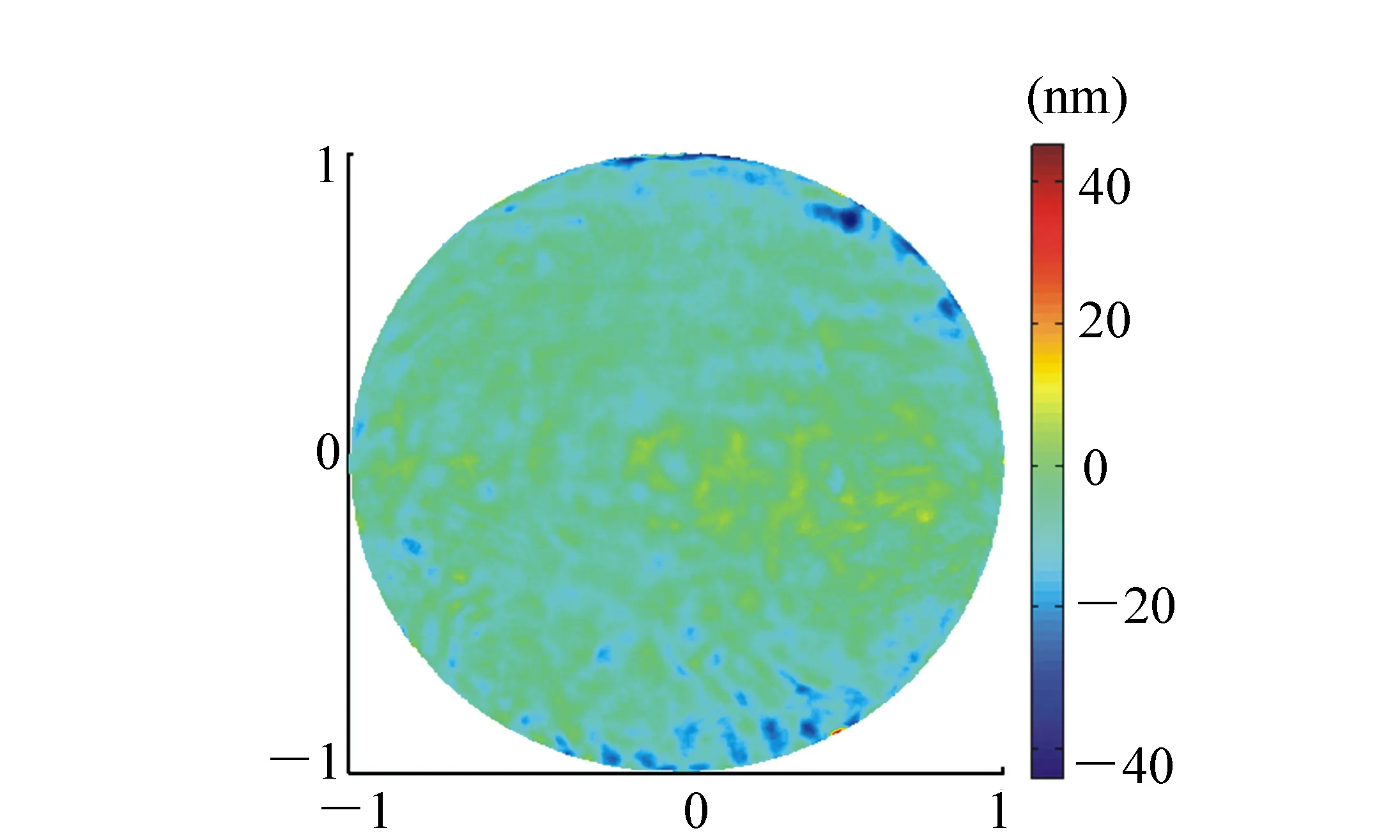
圖15 Ritchey-Common法檢測得到的平面鏡面形(PV=79.1 nm，RMS=11.5 nm) Fig.15 Flat mirror surface shape detected by Ritchey-Common method(PV=79.1 nm，RMS=11.5 nm)

朱碩用Ritchey-Common法對同一塊平面鏡的面形進行檢測[17]，檢測光路如圖14所示，檢測得到的平面鏡面形如圖15所示。將圖12與圖15比較后可知，從整體上來看，兩種方法得到的面形的分布比較相似：在中部偏右的值都比較大，在右上邊緣和右下邊緣處的值都比較小，在其它位置處的值都居中。兩者的RMS值差距也不大，但是PV值差距較大，下面進行詳細分析。

Ritchey-Common法使用的干涉儀的CCD分辨率為1 024 pixel×1 024 pixels，換算到被測平面鏡上，采樣間距和采樣口徑均為1.5 mm左右，而本文的五棱鏡掃描法的平均采樣間距達到了60 mm，采樣口徑達到了27 mm，所以，五棱鏡掃描法的檢測頻率要遠低于Ritchey-Common法。因此，在圖15中，Ritchey-Common法得到的面形的高頻信息較多，面形分布比較散亂；而在圖12中，五棱鏡掃描法得到的面形的高頻信息較少，面形分布比較平滑。注意，在圖15的右下邊緣處有一塊很小的紅色區域(彩圖見期刊電子版)，表示此處有一個面積很小的突起，Ritchey-Common法檢測到了這個突起，它對PV值的貢獻達到了30 nm左右，而五棱鏡掃描法由于檢測頻率較低，所以沒有檢測到這個突起，從而大大減小了PV值，可見，這個突起是兩者的PV值差距較大的主要原因。

將Ritchey-Common法的面形結果作低通濾波后得到如圖16所示的面形，濾波器采用巴特沃斯低通濾波器[20-21]。五棱鏡掃描法的平均采樣間距為60 mm，所以根據采樣定理，低通濾波的截止頻率等于：

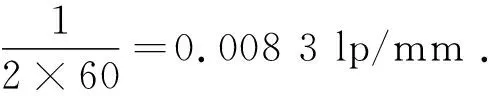
(20)

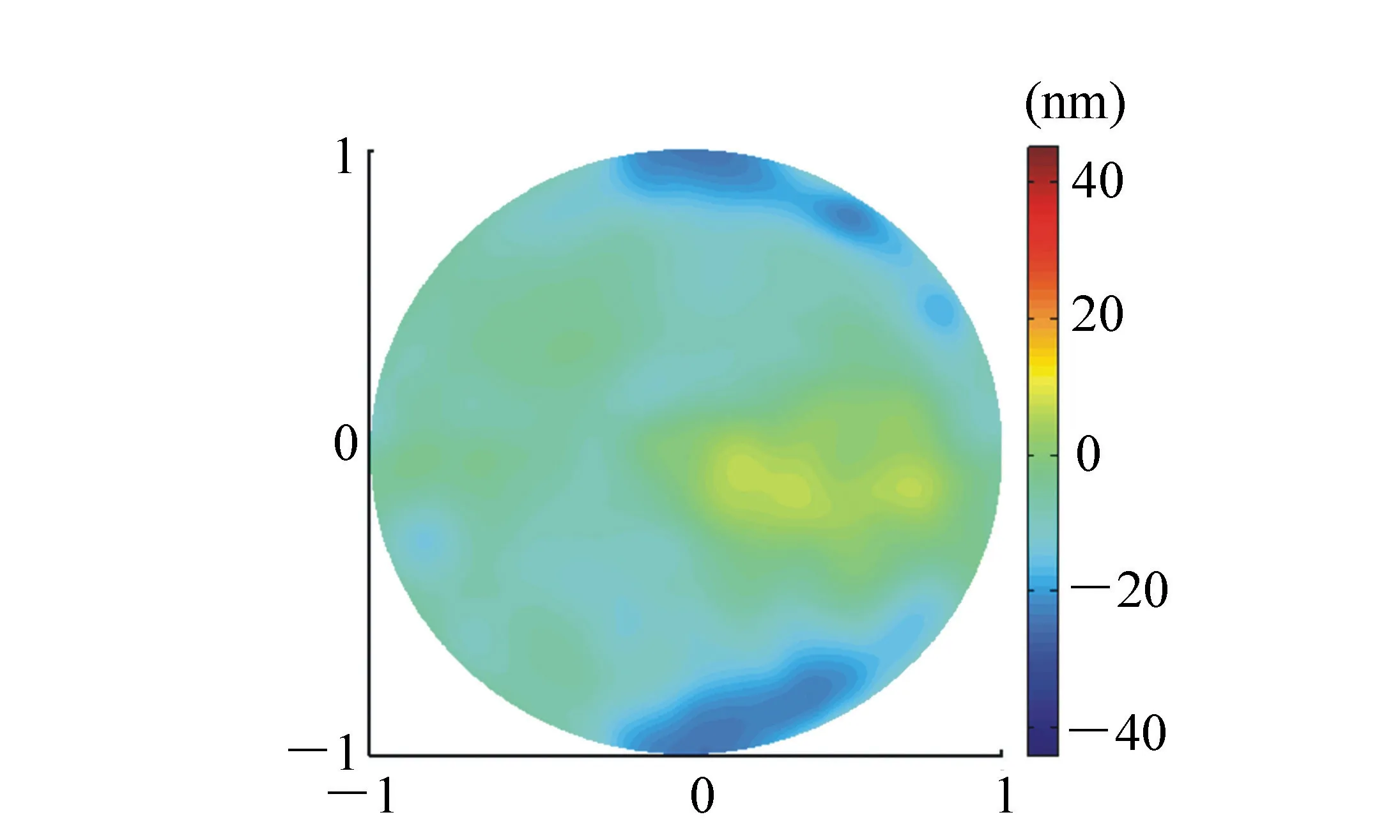
圖16 將圖15作低通濾波后的面形圖 (PV=43.8 nm，RMS=11.9 nm) Fig.16 Surface shape of Fig.15 after low pass filtering (PV=43.8 nm，RMS=11.9 nm)

將圖16與圖15比較后可知，經過低通濾波后，面形變得平滑，由于右下邊緣的突起被濾掉了，所以PV值下降較多，但RMS值變化不大。將圖16與圖12比較可知，與濾波前相比，兩者的面形分布更加相似，都較平滑，PV值也更加接近了。可見，五棱鏡掃描法的面形結果相當于是Ritchey-Common法面形結果的低頻部分。

實際上，五棱鏡掃描法的檢測頻率是可控的，通過減小采樣間距和采樣口徑，增加Zernike多項式的項數，就可以提高檢測頻率；反之，通過增大采樣間距和采樣口徑，減少Zernike多項式的項數，就可以降低檢測頻率。下一步，本項目組計劃提高五棱鏡掃描法的檢測頻率再進行實驗。

另外，在檢測過程中，檢測頻率、采樣間距、采樣口徑以及Zernike多項式的項數這4個參數要相互匹配，這樣才能檢測出該頻率下正確的面形。匹配的原則是：如果需要的檢測頻率較高，則采樣間距和采樣口徑就需要小一些，Zernike多項式的項數就需要多一些；如果需要的檢測頻率較低，則采樣間距和采樣口徑就需要大一些，Zernike多項式的項數就需要少一些。本文根據上述匹配原則，確定了平均最高檢測頻率為0.008 3 lp/mm，平均采樣間距為60 mm，采樣口徑為27 mm，Zernike多項式的項數為36。通過前面所述的仿真分析和檢測實驗已證明這4個參數是相互匹配的。

最后計算得到，圖12與圖15的差值rms值為7.1 nm，圖12與圖16差值的rms值為3.2 nm，均小于五棱鏡掃描法的面形檢測精度7.6 nm rms，可見本文檢測方法是正確的。

6 結 論

本文提出了一種新的五棱鏡掃描法檢測大口徑平面鏡的面形。該方法使用一個掃描的五棱鏡和一個自準直儀測量表面傾斜角的差值，然后建立方程組，最后采用最小二乘法計算得到被測平面鏡的面形。

該方法可以有效減小各種測量誤差：第一，五棱鏡本身的誤差抑制特性以及表面傾斜角差值的計算可以消除傾斜誤差的一階影響；第二，五棱鏡傾斜變化量的監視與調整可以減小傾斜誤差的二階影響；第三，僅使用一個五棱鏡以及表面傾斜角差值的計算可以消除五棱鏡制造誤差的影響；第四， 通過計算表面傾斜角差值、嚴格控制環境以及保證兩個配對點的測量時間間隔較短，可以減小環境帶來的誤差；第五，兩個配對點之間較長的距離可以減小相對誤差。

誤差分析表明，該方法的面形檢測精度為7.6 nm rms。采用該方法對一塊1.5 m口徑的平面鏡的面形進行了檢測，并與Ritchey-Common法的檢測結果進行了對比，兩種方法的面形結果的差異為7.1 nm rms，小于該五棱鏡掃描法的面形檢測精度，證明了利用該五棱鏡掃描法檢測大口徑平面鏡面形的正確性。