構建基本活動經驗 提升數學核心素養

福建省石獅市石光中學 (362700)

李國強

《普通高中數學課程標準(2017年版)》(以下簡稱《課標(2017年版)》指出：通過高中數學課程的學習，學生能獲得進一步學習以及未來發展所必需的數學基礎知識、基本技能、基本思想、基本活動經驗(簡稱“四基”)[1].這是首次在高中課程標準中提出“基本活動經驗”是數學學習的基礎.

數學基本活動經驗，是指學習者在經歷數學學習活動的過程中所獲得的感受、體驗以及由此獲得的知識、技能、情感和觀念的綜合體.數學基本活動經驗是學生個人經驗的重要組成部分，獲得和積累基本活動經驗是提升學生數學核心素養的重要途徑，需要在“做”的過程與“思考”的過程中沉淀.在傳統的課堂教學中，學生數學學習的經驗往往被解題經驗所替代，其數學基本活動經驗不足是一個不爭的事實.筆者認為，重視數學基本活動經驗的積累是對傳統數學學習的一個認識上的提升.學生的基本活動經驗需要在“做”中獲得，在“思”中提升，在“悟”中遷移.以下筆者結合多年的教學實踐，談談在課堂教學中促進學生基本活動經驗積累的幾點體會.

1.在實踐操作活動中喚醒數學基本活動經驗

數學知識的高度凝練性、抽象性等特點，使得學生難以感知和領悟數學知識的意蘊，難以欣賞“冰冷的美麗”，難以把握數學的抽象本質.因此教師需要創設具有生活氣息的問題情境，來喚醒學生的親切感，再借助觀察、操作活動等方式引導學生獲得數學基本活動經驗.因此在課堂教學中，教師可根據教材內容和教學目標，從學生的數學經驗與生活經驗出發創設問題情境，引出數學問題，然后有計劃、有目的地組織學生動手操作、實踐，讓學生在動手實踐中體會數學與生活的聯系，經歷由迷茫困惑到逐步清晰的過程，從而獲得根植于生活“接地氣”的數學基本活動經驗.

案例1 人教A版數學2“二面角”概念教學片斷

師：同學們，初中數學中是如何定義角的？

生：從平面中的一個定點出發引出兩條射線，則這兩條射線和定點組成的圖形叫做角.

師：大家能模仿初中角的定義對二面角進行定義嗎？

生1：將平面中角的概念類比到三維空間，把定點變為定直線(棱)，把兩條射線變為從該棱引出的兩個半平面.

師：對，我們可以類比角的定義得到二面角的定義.將角的定義中每個元素升級到三維空間中的元素，就構成了空間中的二面角.現在大家一起來觀察個種不同類型的二面角.

(教師展示二面角的具體模型，以增強學生對二面角的認識)

師：我們身邊存在二面角模型實例嗎？應該如何刻畫二面角的大小？

生2：課本的書頁與書頁之間就是二面角的空間模型.

師：對，請同學們轉動書頁，思考如何度量二面角？

(學生操作、思考、討論)

生3：既然叫做角，那就需要用一個確定的平面角來度量.

師：你覺得哪一個平面角可以用來度量二面角呢？

(為了破解難點，教師讓每個學生準備一張紙，對折后就是一個二面角.過棱上一點在兩個半平面內嘗試各畫一條射線，然后觀察怎樣刻畫二面角的平面角.小組討論后代表發言.)

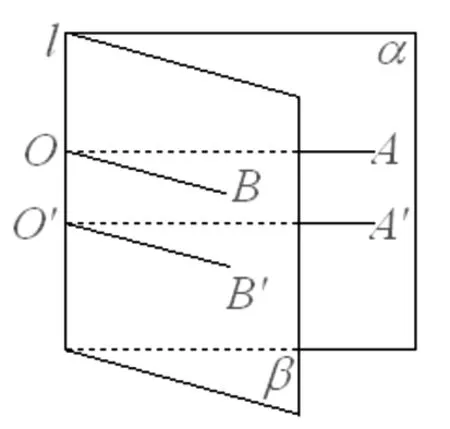
圖1

生4：如圖1，在棱l上取一點O，在兩個半平面內分別作兩條射線OA、OB，使得OA⊥l，OB⊥l，這兩條射線組成的角∠AOB可以刻畫二面角的大小.

師：點O的位置是確定的嗎？能否在棱l上取其他的點？

生5：可以，我在棱l上另取一點O′，同樣在兩個半平面內作兩條射線O′A、O′B，使得O′A⊥l，O′B⊥l，由等角定理得，∠AOB=∠AO′B，所以這樣作出的角只與二面角α—l—β的大小有關，而與點O在棱l上的位置無關.

生6：我是這樣作的：在棱l上取一點O，在兩個半平面內作兩條射線OA、OB，使得OA、OB與直線l的夾角都為60°，這兩條射線組成的角∠AOB也是確定的，所以我覺得∠AOB也可以刻畫二面角的大小.

師：有道理！哪一種方法更合適呢？

師(見學生沉默，教師引導)：請把二面角的一個半平面放在桌面上，另一個半平面繞著棱l轉動，當兩個半平面重合時、兩個半平面都在桌面上時，二面角的平面角分別是多少呢？

(大家動手操作)

生7：當兩個半平面重合時，二面角的平面角為0°；當兩個半平面都在桌面上時，二面角的平面角為180°.此時只有當OA⊥l，OB⊥l時，這兩條射線組成的角∠AOB才是0°、180°.因此當OA⊥l，OB⊥l時，∠AOB表示二面角的平面角最合適.

(學生概括“二面角的平面角”定義)

本環節通過問題情境的創設，增強了數學的趣味性與直觀性.學生通過積極參與，動腦、動手、動口，使活動、思維、語言有機結合，體會用數學的眼光觀察、用數學的思維分析與用數學的語言表達.在此過程中，學生不僅對“二面角的平面角”有了直觀上的感知，提高了空間想象力，而且抽象概括出了“二面角的平面角”的定義.只有這樣，學生獲得的體驗才能更深刻、更牢固，才能實現真正意義上的數學基本活動經驗的有序、自然的生長，而實踐活動本身，也促使學生自然地融入到直觀想象、數學抽象、邏輯推理、數學建模等核心素養的培育過程中.

2.在歸納、演繹中積累數學基本活動經驗

數學學習如果僅僅停留在感性層面的活動經驗，那是很膚淺的，教師需要設置一定的活動方式，將數學思維活動提升到理性層面，以揭示感性經驗背后的理性數學經驗.

性質探究是數學教學中常見的探究活動.教師在引導學生探究性質時，應留給學生充足的時間與空間，引導學生通過操作、觀察、猜想、驗證、提煉，讓學生在主動探究中掌握知識，獲得問題解決的能力，并積累大量的數學活動經驗.

案例2 人教A版數學1“指數函數”圖象性質的實驗探究

活動1 畫出下列兩組函數的圖象.

(1)函數y=2x和y=3x；

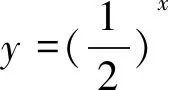
(教師點評學生所畫的圖象，并強調描點法的步驟)

活動2 對于以上兩組圖象，請仔細觀察它們的共同點、不同點與聯系點.

(學生動手操作、分組討論，然后小組代表進行成果匯報.)

小組代表1：函數的圖象都在x軸的上方.

對個別將函數圖象畫到了x軸下方的同學，教師沒有直接點出，而是引導他們利用函數解析式進行自我否定、自我修正，終于得出函數的值域大于0，圖象一定在x軸上方.

小組代表2：函數的圖象都會過同一點(0,1).

小組代表3：指數函數是單調函數：當01時，函數y=ax單調遞增.

師：好！大家還有其它的想法嗎？

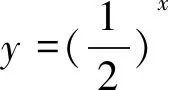
活動3 請學生代表用幾何畫板演示指數函數的圖象與底數a的關系，讓學生進一步觀察指數函數的變化規律.

小組代表5：當a>1時，a越大，圖象越靠近y軸；當0

師：同學們觀察得很仔細！剛剛我們用一些具體函數的圖象特征歸納出了指數函數的圖象性質.但歸納所得到的性質是否正確？我們需要進行證明.請大家從解析式入手驗證，并填寫指數函數性質的表格.(限于文章篇幅，驗證和填表過程略去).

學生通過“作圖——觀察——猜想——討論——驗證——提煉”等過程，得到了指數函數的圖象性質.在此過程中，教師引導學生關注不同的指數函數的“變”與“不變”規律性，將直觀感知與理性思維相結合，體現了從“具體問題出發→觀察、分析→類比、歸納→提出猜想→驗證猜想→演繹證明”的數學發現的一般過程，從中積累經驗，為學生將來的發明和發現奠定基礎，這是數學基本活動經驗提出的初衷[2].

3.在反思體驗中內化數學基本活動經驗

弗賴登塔爾指出“反思是重要的數學活動，它是數學活動的核心和動力”.數學知識所具有的類比與統一的內在聯系特征，使得學生所獲取的數學基本活動經驗具有可遷移性，因此學生個體可以從已有的實踐活動經驗中尋求從事新的實踐活動的“生長點”，但必須給他們留足經驗反思與內化的時空，讓學生經歷反思、感悟、內化等數學活動的全過程，及時總結與提升數學基本活動經驗.長此以往，學生就會“數學地思考”，并發揮一般觀念的思維引領作用，遷移到其他數學知識的學習中，從而促進數學核心素養的發展.

案例3 人教A版數學選修2—1對“橢圓、雙曲線標準方程的推導”過程的反思

教學了橢圓、雙曲線的標準方程之后，教師引導學生學生反思，對公式的推導過程進行“再認識”.

反思1 我們已經學習了橢圓、雙曲線的定義，如何用文字語言和符號語言表示這兩個定義？

反思2 我們還可以進行哪些方程的推導？表示的曲線又是什么呢？

學生躍躍欲試，“探個究竟”的欲望被充分調動起來.

反思的過程是數學活動經驗內化的過程，不僅能加深學生對數學知識內涵與外延的理解，幫助學生形成了對知識與方法的整體性認識，而且為學生積聚了用代數方法研究幾何問題的正能量，有利于培養學生樂于探究、善于質疑、求異創新的精神.一旦自省形式的反思成為學生的自覺行為，“被動接受”就能不斷被“主動生成”所取代，思維能力就能提高到一個由例及類的檔次，從而建立更高層次的認知結構，積累穩定的數學基本活動經驗，并利用這些活動經驗來開啟新知的切入點、挖掘新知的生長點，催生數學核心素養.

總之，學生的數學核心素養的提升不是朝夕之功，而是在數學學習的過程中循序漸進、逐步發展的.因此，數學教學要讓學生親身經歷數學活動的過程，并發揮學生共同體的作用，充分利用討論、交流學習等方式，促進個體經驗的交流與融合，從而幫助學生獲得和積累最具數學本質的、最具價值的數學基本活動經驗，從而讓數學核心素養在數學教學中落地生根.