平和創新 樸實靈動*
——2018年江蘇高考數學第13題評析與教學啟示

江蘇省板浦高級中學 (222241)

李忠貴

高考數學試題凝聚了專家的集體智慧和大量心血，是豐富的“寶藏”.對高考題(特別是壓軸題)進行深度研究，有利于領會其命題規律、設計意圖、選拔功能，感悟數學的育人價值，從而把握教學的方向，找準教學中存在的問題，實施教學變革，實現高效教學.下面是筆者對一道高考題的深刻思考，期待對今后的教學有所啟迪.

一、試題

在△ABC中，角A,B,C所對的邊分別為a,b,c，∠ABC=120°，∠ABC的平分線交AC于點D，且BD=1，則4a+c的最小值為．

二、評析

1.試題立意

本題為文理合卷的填空題第13題，為壓軸難題，涉及高中數學眾多核心(主干)知識，比如基本不等式、平面向量的數量積、角平分線性質、余弦定理、三角形面積計算公式、導數、三角函數定義及性質、同角三角函數關系等，它們在《2018年江蘇省數學高考考試說明》中要求均為B、C級要求，凸顯了對核心內容重點進行考查的命題思路，彰顯了在知識網絡交匯處命題的設計理念，考查了數形結合、函數與方程、轉化與化歸等數學思想以及邏輯推理、數學運算、數學抽象、數學建模等核心素養，充分體現了以考查“核心素養和創新思維”為重點的命題導向，問題構思自然，設計精巧，獨具匠心.

2.試題表達

試題以斜三角形和多元函數最值的背景呈現，考生十分熟悉，試題表達清晰，簡單明了，降低了閱讀量，進而減少了閱讀時間和緩解考生的心理壓力，這些給考生以簡潔中見關懷、平和中見親切.思考與求解過程中卻又能感受到本題的創新之處，這也為優生提供了展示的空間，凸顯了壓軸試題良好的效度和區分度.

3.試題來源

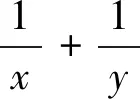
命題專家以上述必修五兩道課本題為藍本，以斜三角形為載體，進行變式、重組、創新設計，從而得到本試題.

4.試題傳承

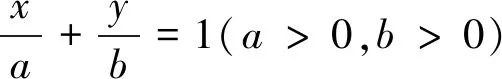
以上題都是多元函數的最值問題，而本試題更靈活、難度也變大，體現了良好的傳承.

5.試題解法

從條件和結論的內在聯系知，求解分兩步：

(1)由已知條件推導a與c相互關系；(2)在此基礎上求4a+c的最小值.

第一步：推導a與c的相互關系.

思路一：挖掘圖形中隱藏的面積關系，再利用已知條件分別進行表達，則問題可輕松解決.

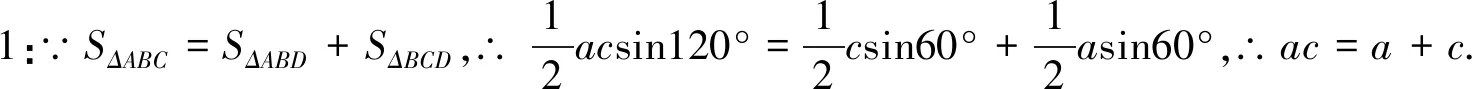
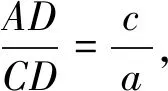
解法2：在ΔABD和ΔBCD中，由余弦定理得

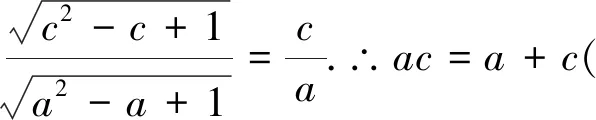
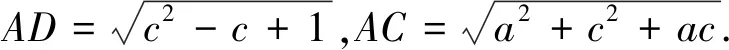
思路三：對于幾何圖形問題，可利用已知條件恰當建系，運用代數方法進行處理.

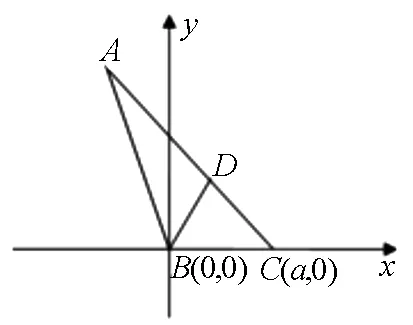
圖1

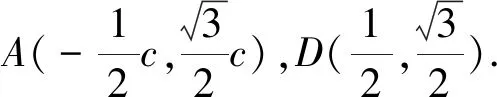
圖2

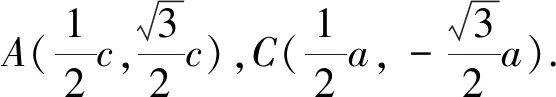
思路四：向量的模本質為兩點間的距離，向量的數量積活化模的求法.因而可利用平面向量基本定理、向量的數量積及角平分線性質進行轉化.

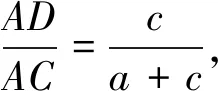
第二步：由a與c等量關系求4a+c的最小值.

思路一：由目標的結構特點，再結合a與c的等量關系，容易聯想到基本不等式.而目標為“求‘和’的最小值”，必須合理變形，配湊出“‘積’為定值”.

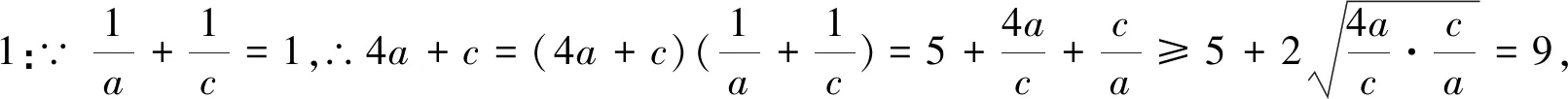
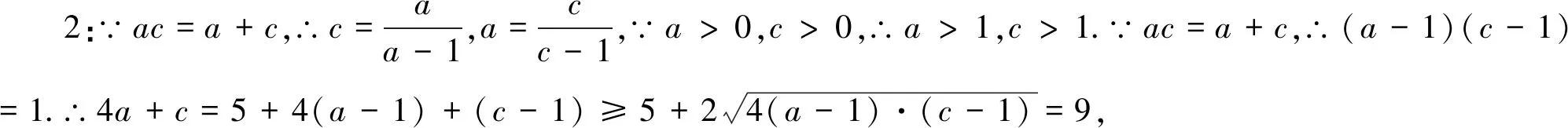
思路二：由a與c等量關系特點，可通過減元或換元，將多元函數化為一元函數，可輕松配湊出“‘積’為定值”，則難點得以突破.

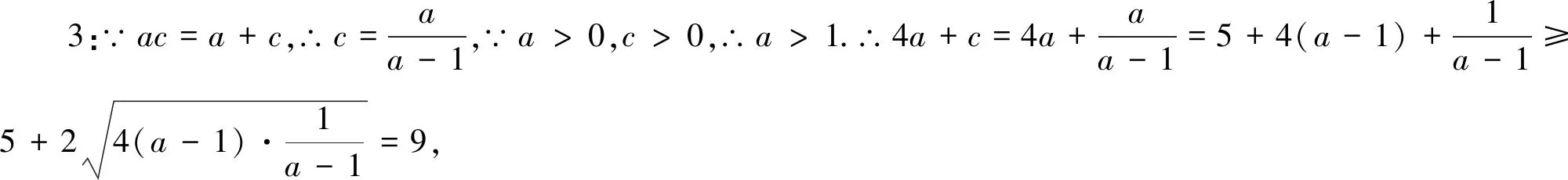
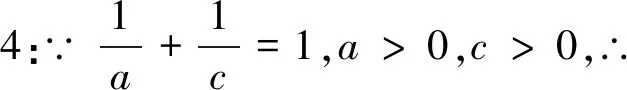
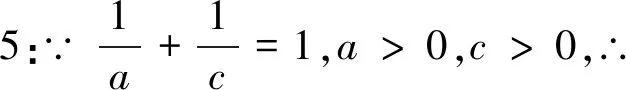
思路三：由a與c等量關系，合理減元，將多元函數化為一元函數.由于此函數不是基本函數，可借助導數確定其單調性，進而求出最小值.

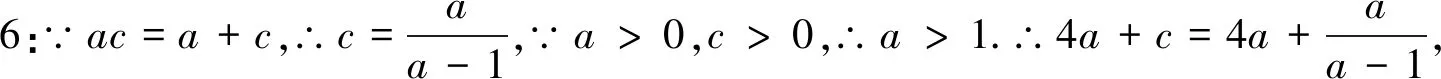
思路四：由a與c等量關系，合理減元后，將函數問題轉化為一元二次方程，利用判別式進行求解.

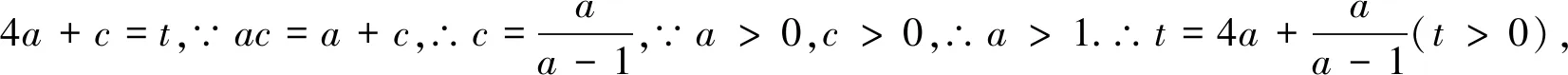
思路五：由a與c等量關系和目標的結構特點，聯想到向量數量積性質，從而構造向量進行求解.

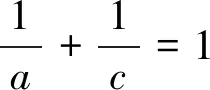
思路六：由a與c等量關系和結論的內在聯系，聯想到柯西不等式，進行求解.

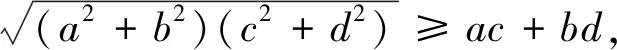
解法反思：

①第一步解法：有的挖掘圖形中隱含的面積等量關系，有的利用角平分線性質和余弦定理，有的恰當建立坐標系，有的構造平面向量并利用向量的數量積求解等，以上解法均從核心知識及其內在聯系出發，用數學的眼光去思考與求解問題，運用數形結合、轉化與化歸等數學思想方法實現合理轉化，這是求解數學問題的通性通法；

②第二步解法：有的通過“1”的代換、三角換元、均值換元、減元等配湊出“積”為定值，從而使用基本不等式進行求解；有的通過減元，將多元函數的最值問題化歸為一元函數的最值問題，使用導數法求解；有的運用函數與方程思想，利用一元二次方程有正根的條件求解；有的巧妙構造平面向量，運用向量的數量積性質，問題可輕松求解；有的根據問題的結構特點，利用柯西不等式等.

以上解法盡顯“數學味”，彰顯學生的核心素養和關鍵能力.因而本試題及解法平和創新，樸實靈動.

6.求解陷阱

(1)陷阱之一：方法自然但難以求解.

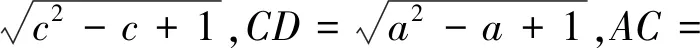
(2)陷阱之二：兩次用公式導致錯解.

錯因分析：∵不等式(1)等號成立的條件為a=c,不等式(2)等號成立的條件為4a=c，∴兩個等號無法同時成立，∴4a+c>8,∴4a+c的最小值不為8.

三、教學啟示

1.用好課本例(習)題，揭示其隱含價值

課本是眾多專家依據教學大綱反復打磨編寫的系統闡明數學內容的教與學用書，它不但是教師教、學生學的關鍵，而且是各種考試(尤其是高考)試題命題的主要來源.有的教師認為“課本例(習)題簡單，難以應對高考，沒必要花時間去研究，不如多講、多練一些教輔資料上難題更實惠”，顯然是錯誤的.教師應深度研究教材，把握編寫專家的意圖，發揮例(習)題的示范性、典型性，并對其拓展延伸，挖掘其蘊含的教學價值、隱藏的重要結論、數學方法、數學思想、研究方法、數學本質、數學文化、育人價值等，對啟迪學生思維、發展學生關鍵能力、提高數學解題效率等大有裨益.

2．讓學生自主建構知識，突出對其本質的探索

高考的壓軸題，常常涉及的是多元的概念、原理與公式.如何深刻理解這些知識點，弄清其內在聯系，并能創新應用，本身就需要一定的智慧，單靠大量刷題或者死背硬記肯定難以奏效.知識不是教師告訴學生的，也不是學生看書得到的.這就需要教師在教學中恰當創設教學情境、精心設計問題，深度引領學生自主探究，自主建構知識，讓學生學習數學的過程變為在教師誘導下“再發現”過程；同時孤立的知識無法形成能力，教師要讓學生感悟核心知識的交匯之處，幫助他們建立和體會完善的知識網絡體系；為提升學生的應變能力，教學中教師應著力培養他們追問知識及問題本質的習慣.如為什么要學習基本不等式？基本不等式的功能是什么？它的本質是什么?應用它求解問題應注意哪些？...

3.關注核心素養培養，重視學生的感悟反思

無論哪種課型，教師的講還是學生的練，都需要教師緊扣教學目標，貼近學生最近發展區，運用教學智慧，以素養立意，從整體精心設計.為什么選擇這個問題？想培養學生哪些能力？發展哪些核心素養？這種解法如何自然呈現？是否可一題多解？多種解法能否歸一？多種解法的本質、核心及其內在聯系又是什么？最優解及通性通法又是什么？可否進行一題多變？可否設計多題歸一？要謹防教學(特別是高三教學)形式單一化，不是“講練講”就是“一講到底”，或者是“練講練”，學生疲于應付.因為所有素養和能力的提升最終都要通過學生的自我感悟反思來實現,所以要給學生留有足夠的時間和空間，讓他們經歷理解、反思、總結、提煉、內化、感悟的思維歷程.