高溫作業專用服裝的最優設計

張宗渝 田大雕 王可豪

摘要：本文基于傳熱學理論，通過構建數學模型研究了高溫作業專用服裝的設計問題。我們將服裝簡化由三層織物材料構成，記為工、Ⅱ、Ⅲ層，第Ⅲ層與皮膚之間還存在空隙，將此空隙記為Ⅳ層。首先，將熱傳遞過程視為一根均勻同性桿的傳熱，考慮熱傳導和對流兩種方式，再基于能量守恒和傅里葉定律，對前三層材料建立了一階熱傳導偏微分方程的數學模型;對第Ⅳ層，建立了一階耦合熱傳導對流方程的偏微分方程的數學模型，利用熱傳導方程的有限差分法求數值解。在環境溫度為75℃、Ⅱ層厚度為6mm、Ⅳ層厚度為5mm、工作時間為90分鐘的情況下，通過估計參數和一些已知的數據，利用MATLAB仿真出每一層的溫度變化分布圖，求得假人皮膚外側的溫度;在環境溫度為65℃、Ⅳ層的厚度為5. 5mm，確保工作60分鐘，皮膚外側溫度不超過47℃，且超過44℃的時間不超過5分鐘情況下，基于反問題的基本理論，在熱傳導模型基礎上，建立優化模型，再利用遺傳算法，求出第Ⅱ層的厚度在區間[5，25]上達到要求。最后，在環境溫度為80℃，確保工作30分鐘，皮膚外側溫度不超過47℃，且超過44℃的時間不超過5分鐘的前提下，利用相同模型求出第Ⅱ層的厚度在[11，12.8]和第Ⅳ層的厚度在[3.5，6]區間上達到要求，通過構造初始函數，得到了與真實數據吻合的結論。

關鍵詞：一階熱傳導方程;一階耦合熱傳導對流方程;有限差分方法;遺傳算法

1引言

在高溫環境下工作時，人們需要穿著專用服裝以避免灼傷。因此，本文以專用服裝的設計為目的，構建數學模型，以較低成本研發出合格的服裝，這對保護工作人員的生命安全有著十分重要的意義。

2 問題重述（略）

3 模型假設

1）熱傳遞垂直于皮膚方向進行，故可視為一維的;

2）服裝材料只考慮傳熱方式，第Ⅳ層為熱傳導和空氣的對流兩種方式;不考慮濕傳遞，即忽略水汽、汗液的影響;

3）熱傳導熱傳遞到織物的過程中是均勻的，且熱防護材料沒有發生溶解;

4）專業服裝材料內部無水分，各層材料之間沒有空氣層，而且是均勻各向同性的，即考慮成一根均勻同性桿的熱傳導。

4 模型的建立與求解

4.1 熱傳導模型

在固定的環境溫度、時間、已知Ⅱ、Ⅳ層的厚度等情況下，該過程類似一根均勻同性桿的熱傳導[1]。因此，可將其溫度分布簡化為圖1所示。

熱量守恒定律可表示為

溫度變化吸收的熱量一通過邊界流入的熱十熱源放出的熱量，根據傅里葉熱傳導定律有[2]

其中熱傳導系數k假設是常量，熱量公式為

Q= cmu

（2）

取材料內任一點處垂直于皮膚方向的微元線段L，微元上t1，t2時刻各點溫度分別表示為u（x，t1），u（x，t2），則L內溫度變化的熱量Q滿足

4.2熱傳導模型的求解

首先由題設，可得出定解條件和初值條件分別為

u（0，0）=ua

u（x，0）=φ（x）

（10）其中φ（x）是連續函數，但該函數目前很難估計。為解決問題，我們假設所建立的偏微分方程的解一定存在。

定理（解的存在性）[3]若（φ（x）連續，則存在常數M>0和A>0使

u（x，0）=φ（x）

（11）成立，則方程（8）滿足初值條件的解存在。

由解的存在定理，我們取

|φ（x）|≤MeAr2

（12）

以保證解存在，初步的計算后，得到（8）式解的結果，見圖2，同時根據題目中的測量值，給出溫度變化情況，見圖3。

由圖可得，曲線的凸性是相反的。為改變凸性，利用曲線關于直線y=x對稱及平移的原理[4]，對（4）式求反函數及平移，得

基于文獻中的有限差分法[5]，以及附件中的數據，適當選取模型中的參數（見表1）。

4.3耦合熱傳導對流模型

由于第Ⅲ層與皮膚之間存在氣體，故第Ⅳ層在原本的熱傳導方程上，增加對流的情況，建立耦合熱傳導對流模型

對于第Ⅳ層，由參考文獻[6]，當厚度不超過6.4mm時，對流形式的熱傳遞影響是很小的，因此，忽略對流的影響，利用MATLAB求解得到了第Ⅳ層溫度分布，如圖6。

4.5優化模型

當環境溫度為65℃，Ⅳ層厚度為5. 5mm時，需確定第Ⅱ層最優厚度，確保工作60分鐘，假人皮膚不超過47℃，且超過44℃的時間不超過5分鐘。作為熱傳導的反問題，由于反問題具有非線性、不適定性等特點，使反問題的求解比正問題復雜得多[7]。在反問題中，將材料的邊界條件或物性參數作為優化變量，把正問題得到的計算值作為目標函數求極值。因此，我們將反問題的目標函數設計為熱傳導模型（16），第Ⅱ層材料的厚度為極值點。于是，目標函數為

minu（x，t）

（17）

約束條件為：

1）當時間t為0≤t≤55時，溫度應滿足

u（x，t）≤44

（18）

2）當時間f為0

u（x，t）≤47

（19）

從而可建立優化模型

minu（x，t）

（20）

根據（21）式，可確定極小值點，即第Ⅱ層的厚度。

當環境溫度為80℃，確定第Ⅱ層和第Ⅲ層的最優厚度，確保工作30分鐘，假人皮膚外側溫度不超過47℃，超過44的時間不超過5分鐘，增加了一個變量，可以用與（21）式相似的方法建立模型并求解。

同理，在新的約束條件

4.6優化模型求解

根據下文給出遺傳算法步驟進行求解[8]。

Stepl確定每個反演參數的定義域，即搜索區域。

u≤44，0≤t<55

（24）

u≤47，55≤t≤60

（25）

Step2確定遺傳算法的相關參數。

Step3利用迭代生成的值修改有限差分法子函數中的參數，并對之進行求解，獲得相應的溫度場。

Step4將計算值帶入函數中，如果滿足收斂準則，則迭代結束;否則更新種群并返回第三步。

各層模型中參數的取值見表2。

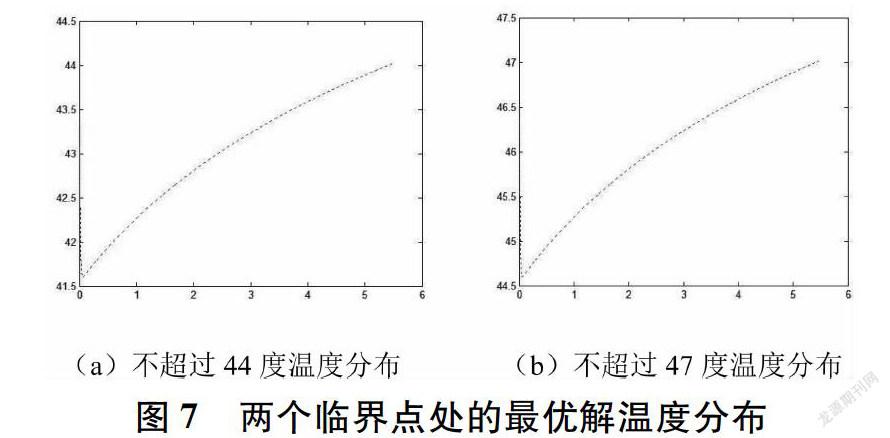
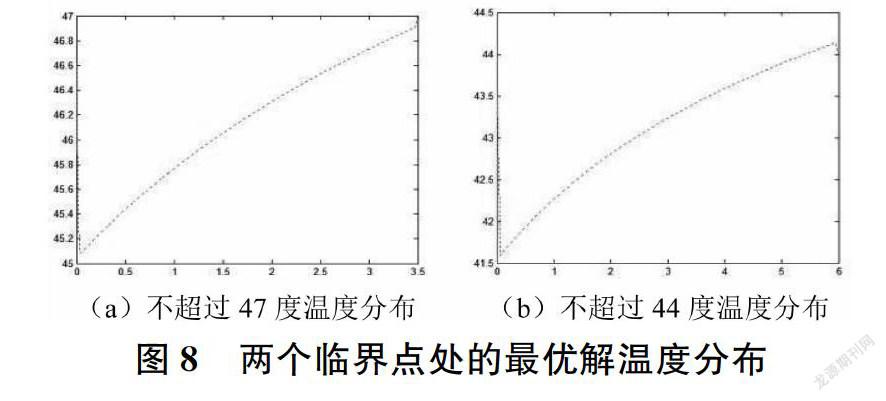
當第Ⅱ層的最優厚度x∈[5，25]時，兩個臨界點處的最優解溫度分布見圖7。 同時，當第Ⅱ層的最優厚度x∈[11，12.8]，第Ⅳ層的最優厚度為x∈[3.6，6]，即滿足環境溫度為80℃，工作時間為30分鐘時，假人皮膚外側溫度不超過47℃，且超過44℃的時間不超過5分鐘，最優點處的溫度分布，見圖8。

5 模型評價

本文利用傅里葉熱傳導定律建立數學模型，研究物體的熱量變化，通過熱量守恒定律，建立關于溫度對時間與厚度的偏微分方程，從而提高了真實可靠性;運用遺傳算法，得到了較準確的最優解;通過MATLAB對所求解析式方程進行處理，得到所需要的圖形走勢，使結果更加的具有說服力與真實性。缺點是沒有考慮物體在熱傳導的時候，熱量對其它物體之間進行的熱交換，并且在建立模型的時候也僅僅在平面的角度上考慮問題。

（指導老師：馬志霞）

參考文獻

[1]陳金靜，耐高低溫柔性多層隔熱材料結構與隔熱性表征，東華大學博士學位論文，2010年。

[2]俞昌銘，熱傳導及其數值分析[M]，北京：清華大學出版社，1981年。

[3]趙鎮南，傳熱學（第二版）[M]，北京：高等教育出版社，2008年。

[4]俞昌銘，傳熱學[Ml.北京：高等教育出版社，1984。

[5] Gao.Z.，X.Fa，and L Bian. ，An Analytical Solu-tion to One Dimensional Thermal ConductionConvection in Soil，Soil Science， 2003.

[6]陳祖墀，偏微分方程（第三版）[M]，北京：高等教育出版社，2009年。

[7]史策，熱傳導方程有限差分法的MATLAB實現，咸陽師范學院學報，2009年，Vol. 24，No.4，P27-29。

[8]潘斌，熱防護服裝熱傳遞數學建模及參數決定么問題，浙江理工大學碩士學位論文，2016年。