基本平面圖形的再研究

張路燕

摘要：隨著現代化教學的進程不斷加快，促使一線教師的我們在教學中必須深入思考，認真挖掘，讓教學更加科學化、先進化，在傳道授業的同時，更加要注重學生核心素養的養成與深化。在新課程的理念下，我們從七個方面對北師大版七下數學《基本平面圖形》進行說明：教材分析、學情分析、目標分析、教學方法、教學設計、教學策略、中考趨勢。每個環節層層遞進，很好的體現了新課程改革以生為本、師生互動、生生互動的理念，從中為邏輯推理能力的養成奠定堅實的基礎。

關鍵詞：現代化課堂 邏輯推理能力 以生為本

隨著新課程改革的深入，新課程教學理念所呈現出的科學性、先進性以及學習理念、學習方式等的不斷變化，促使教師必須打破傳統教學的圍欄，努力去實踐新課程理念，探索出適合學生人生觀、價值觀以及認識觀不斷變化的教學方式，讓課堂教學綻放出新光芒。下面我就北師大版七年級數學《基本平面圖形》，進行簡單說明，層層說明學生邏輯推理能力的養成過程。

從新舊課標的對比我們可以發現：新課標將原“空間與圖形”更名為“圖形與幾何”，名字更加的具體，并且對基本事實“兩點確定一條直線”，“兩點之間線段最短”提高到掌握的要求，將其能很好的應用在生活實際，體現了數學源于生活，應用于生活的理念。圍繞新課程改革理念，新課標要求，從以下七方面對本章進行簡要說明。

一、教材分析

1、新舊教材內容對比

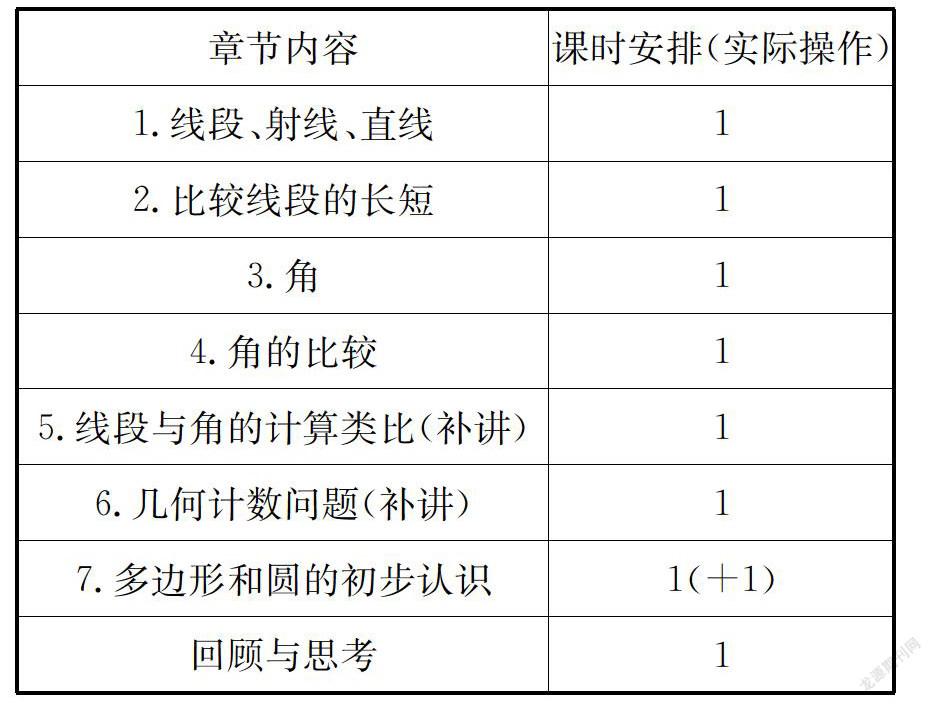
由上圖可知，舊版教材第四章的題目“平面圖形及其位置關系”，新版教材削弱了對位置關系的要求，更名為“基本平面圖形”，相應的減少了與位置關系有關的小節，增加了“多邊形和圓的初步認識”，課時安排上，每節課傳統課時基本沒有變化，總課時由7節調至5節。

2、教材編寫意圖

本章是義務教育數學課程標準北師大版教科書七年級上冊第四章，內容圍繞了解基本幾何元素展開，以“基本幾何元素表示度量多邊形和圓的初步認識”為線索，力求呈現有關的概念背景，突出對生活經驗的抽象，關注線段與角的度量在方法上的一致性。

在基本幾何元素的基礎上，新增內容”多邊形和圓的初步認識”，使學生在具體的情景中認識多邊形、正多邊形、圓、扇形等基本的平面圖形及其相關概念，為后續學習做鋪墊。

3、知識結構

本章內容由現實情境引入，抽象出基本平面圖形，描述性給出基本圖形的相關概念，其中重點強調線與角的符號表示、度量計算及基本事實，多邊形和圓由以前第一章整合至第四章，增加了對正多邊形的學習。

4、地位與作用

知識層面：有關線與角的概念、性質、表示方法、作圖、計算等，都是重要的幾何基礎知識，是后續學習研究幾何圖形的基礎。能力層面：小學通過動手操作活動，學生具備簡單的動手操作、識圖作圖能力。在此基礎上，培養學生觀察、分析、概括等初步能力。情感層面，本章提供了大量生動有趣的現實情境，激發學生對基本圖形學習的興趣。培養學生良好的情感態度和主動參與、合作交流的意識。

二、學情分析

小學階段，學生已經初步認識了線段、射線、直線與角的相關知識，并且在七年級第一章感受了數學與現實的緊密聯系，具備了學習基本平面圖形的知識基礎。學生通過小學階段簡單圖形的認識，和第一章豐富的圖形世界學習，具備合作、交流的學習能力，畫圖、制作模型的操作技能，以及初步觀察、歸納的經驗。。我校學生基礎知識較扎實、思維較活躍，能積極參與問題的討論，并且能進行一定的抽象概括，具備一定的文字、符號和圖形語言的轉化能力。

三、目標分析

根據新課標要求及我校學生特點，分別制定以下目標：

1、教學目標：

1）知識與技能目標

（1）認識線段、射線、直線、角、多邊形、扇形、圓等簡單平面圖形，了解其含義及相關的性質。

（2）能用符號表示線段、射線、直線、角。

（3）會比較和計算線段長度和角的大小。

（4）能用尺規作圖作一條線段等于已知線段長。

2）過程與方法目標（數學思考與問題解決）

（1）通過類比學習線段和角的計數，利用線段中點、角平分線的定義、性質以及和、差、倍、分等關系進行相關計算，經歷借助圖形思考問題的過程，初步建立幾何直觀。

（2）通過尺規作圖，加強動手操作能力。

（3）通過豐富的實例，體驗基本平面圖形的抽象過程，積累幾何活動經驗。

3）情感態度價值觀

（1）感受圖形世界的豐富多彩，體驗數、符號和圖形是描述現實世界的重要手段。

（2）感受數學的美，使學生感受數學美學的應用價值。

2、教學重點和難點

1）教學重點：

（1）認識線段、射線、直線、角、多邊形、扇形、圓等簡單基本圖形，了解其含義及相關性質。

（2）能用符號表示線段、射線、直線、角。

（3）掌握線段的長度和角的大小的比較和計算方法，會進行角的單位的簡單換算。

（4）能用尺規作圖作一條線段等于已知線段。

2）教學難點

（1）從現實情境中抽象幾何圖形。

（2）線段、射線、直線、角及多邊形對角線的計數問題。

（3）線段的長度及角的大小的和差計算。

3）突出重點和突破難點的策略

（1）結合現實情境，理解抽象概念，化抽象為直觀進行教學。

（2）通過動手、動腦、多觀察、多分析，培養識圖、動手操作能力，進一步了解圖形的有關特征。

（3）重視數學思想方法的滲透，將線段、角的計算變式類比，突出類比思想，從而突出重點，突破難點，

四、教學方法

1、本章以“探究——發現”教學模式為主，并輔以其他教學模式。

2、教師的教法：突出聯系生活實際，利用學生所熟悉的一些圖片圖形，激發學生的興趣，精心組織探究活動，通過師生、生生的交流互動，從而引導學生認識基本圖形，了解基本圖形的簡單性質，為今后空間與圖形的進一步學習打下堅實的基礎。

3、學生的學法：突出觀察發現，注重學生間的交流探究與動手操作，在探究活動中，歸納總結并掌握相關知識，從而認識基本圖形，并形成良好的學習習慣。

五、教學設計

1、教學計劃

根據我校學生特點，對本章內容作適當調整，線段與角的計算是今后圖形與幾何學習的一個重要基礎，可以幫助我們養成按照一定順序去觀察、思考問題的良好習慣，故建議教師在此增加2課時，作專題研究，課本安排6課時，實際操作9課時。

2、案例剖析及學法指導

幾何知識學習，一般從以下四方面人手：基本概念、公理與定理，圖形性質與判定，幾何計算。本章內容對應分為：①基本概念：線段、直線、射線、中點、角、角平分線、多邊形、正多邊形、圓和扇形;②公理：直線公理、線段公理;③性質判定：中點性質及判定、角平分線性質及判定;④計算：幾何計數、線段長度、角的大小。其中，基本概念易于理解，單獨學習公理也較好理解，若將兩個公理放在一起考察，學生易錯易混，性質判定易錯易混，計算是難點。

在教學中，呈現易于理解點主要從情境出發，使學生自主探究、合作交流。

在解決易錯易混點時，注重線與角的符號表示，重視數形結合思想在解題中的運用，更要加強類比教學。

3）學法指導

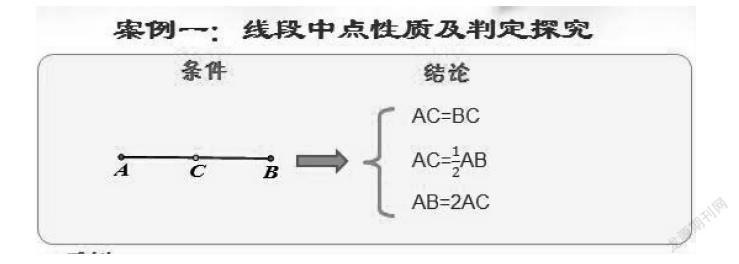
以線段中點判定為例，已知條件點C是線段AB的中點，學生通過觀察，易知三條線段的關系。

將條件和結論互換，設計小組活動，使學生探討其命題的正確性，通過交流，學生易舉出反例，得出點C在線段AB上時，命題成立。由于線段和角的研究具有相通性，通過類比，學生易得出角平分線判定條件，強調射線在角內。

計算是圖形與幾何部分的難點之一，為更好的突破難點，必須充分發揮學生的主動性，以數線段為例，引導學生通過形象作圖，總結計數方法，從特殊到一般窮舉歸納，從而得出結論。

將數線段條數經過適當轉化，可轉化為數三角形個數和數角個數，利用轉化思想引導學生學習是一種重要的數學教學方法，可以很好培養學生數學能力，并用于解決諸如車票、球賽、打電話等實際問題。在幾何計數問題上，可依照學生特點和層次，進行拓展學習，如n個點最多可畫出多少條直線。

六、教學策略

我們從兩方面進行研究。

1、基本圖形研究

研究線段和點的位置關系主要從兩方面進行，點在線段上與點在線段的延長線上。當點C在線段上時，有中點問題，三等分、四等分點等，由此可延伸到三角形面積等分問題。

回歸一般情況，是我們常見的雙中點距離問題。如圖，當點C在線段AB上時，可令AC=a，BC=b，取線段AC，BC的中點M、N，顯然，MC= 1/2a，CN=1/26，故MN=1/2（a+b）。當點C在線段AB延長線上時，運用多媒體技術，展示點C在直線AB上的運動過程，當點C在直線AB上運動時，兩中點距離與點C位置無關，都為線段AB的一半。

根據學生特點，對線段問題可做進一步橫向拓展，討論線段CD在線段AB上，CD與AB交錯，CD在AB的延長線上，教師可作深一步研究，此時兩中點的距離為1/2（AB+CD），與線段CD位置無關。

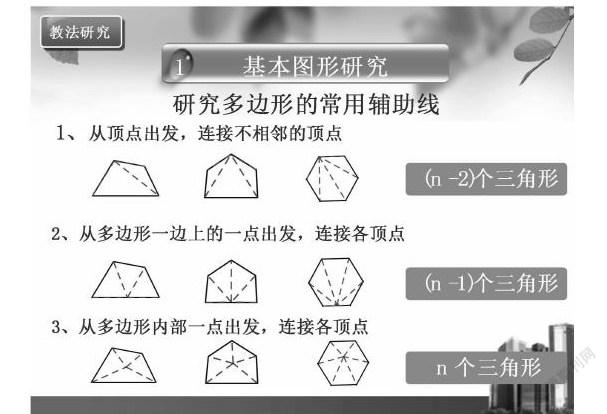
在研究角的問題中，我們常常將其類比線段進行研究，得到類似的結論。本章除線與角的研究外，還有新增內容多邊形，根據點的位置，我們可以采取如下三種方式分割，把多邊形問題轉化為三角形問題，將復雜問題簡單化是數學學習的一個重要思想。

2、數學思想方法應用

數學思想的滲透，是數學教學的重要方面，除前面涉及到的轉化思想、類比思想、整體思想，還有分類討論思想和方程思想。

在分類討論思想中，強調幾何作圖，突出分類標準，以點在線段上和點在線段延長線上分類;對于角，以射線在角內或角外進行分類。在線段與角的計算中，比例問題是常見題型之一，除了用小學的算術方法外，更可設未知數，建立方程，可以很好的簡化解題步驟，突出方程思想，為后續學習作鋪墊。

七、中考鏈接

本章屬于最基礎的幾何內容，側重于基本概念的建立，在中考中以“雙基”考察出現，中考命題圍繞基本概念、性質識別、簡單計算、探索規律等方面出題。

本章是圍繞圖形與幾何的基礎，在教學中要特別注重學生興趣的培養，要使學生感受到身邊處處都有基本圖形，處處都有基本圖形展現的數學美。教學注重新課程教學理念的體現，學生為主體，注重動手操作，體現學生的主體性。教學明確教師的地位和作用，教師是教學活動的設計者，教師是教學活動的組織者和引導者，教師和學生共同探討，促進教學。教學注重概念的學習，本章內容的概念性質和判別較多，學生容易混淆，讓學生從生活情境中形成對概念的全面認識。教學注重數學思想方法的滲透，本章的設計特別強調數學知識和技能的訓練，滲透了數學結合的思想、轉化思想、從特殊到一般的思想、分類思想、類比思想等。

著名數學家米山國藏有這樣一段名言：“學生所學的數學知識，在進入社會后幾乎沒有什么機會應用，因而這種作為知識的數學，通常在走出校門后不到一兩年就忘掉了，然而不管他們從事什么工作，惟有深深銘刻于頭腦中的數學的研究精神，數學思想和方法會隨時的發揮作用，使他們受益匪終身。”“授人以魚，不如授人以漁”，因此我以為我們的使命，不僅是教會學生基本的數學知識和如何解題，更重要的是引導學生學會如何進行數學問題的研究，如何將數學應用于生活，這也許就是新課改的理念，新課改的希望。

參考文獻

[1]北師大版七年級上數學教材，北京師范大學出版社出版

[2]義務教育階段數學課程標準（2011年版），人民教育出版社出版