遷移經驗，提高“四能”

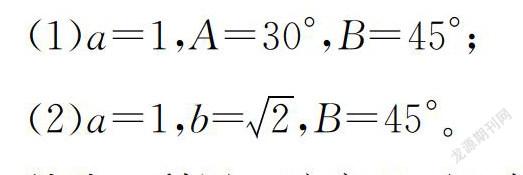
摘要：基本活動經驗是指學生親自或間接經歷了活動過程而獲得的經驗，需要在“做”的過程中體驗，在“思考”的過程中沉淀，是在數學學習活動過程中逐步積累的。形成和積累基本活動經驗，是提高“四能”的有效手段，也是發展數學核心素養（“三會”）的基本方法。在教學過程中，教師要善于創設合適的問題情境，引導學生遷移已有的活動經驗，發現、提出問題，并在新問題的分析、解決過程中不斷積累新的活動經驗，進而發展數學核心素養。以《正弦定理》第一課時為例加以說明。

關鍵詞：基本活動經驗學習遷移四能正弦定理

《普通高中數學課程標準（2017年版）》指出：通過高中數學課程的學習，學生能獲得進一步學習以及未來發展所必需的數學基礎知識、基本技能、基本思想、基本活動經驗（簡稱“四基”）。基本活動經驗是指學生親自或間接經歷了活動過程而獲得的經驗，需要在“做”的過程中體驗，在“思考”的過程中沉淀，是在數學學習活動過程中逐步積累的。形成和積累基本活動經驗，是提高“四能”的有效手段，也是發展數學核心素養（“三會”）的基本方法。在教學過程中，教師要善于創設合適的問題情境，引導學生遷移已有的活動經驗，發現、提出問題，并在新問題的分析、解決過程中不斷積累新的活動經驗，進而發展數學核心素養。下面以蘇教版高中數學必修5《正弦定理》第一課時為例，談一些體會。

一、整體建構

用正弦定理解三角形，是初中解直角三角形的推廣，故遷移解直角三角形的活動經驗，用“化直”（包括借“高”化直和借“圓”化直）

的想法去研究，是一種自然的想法。另外，正弦定理的課程安排在“三角”“向量”知識之后，因此，借助向量的工具作用引入角，并研究幾何問題，也是一種合適的選擇。同時，用正弦定理解三角形，是典型的用代數的方法來解決幾何問題，故解析法研究順理成章。基于這樣的學習經驗，正弦定理的學習內容整體建構如圖1所示。

二、教學設計

（一）創設情境，提出問題

導語法國數學家傅里葉有過這樣的名言：對自然界的深刻研究是數學發現的最自然的來源。從金字塔的建造到尼羅河兩岸的土地丈量，從大禹治水到都江堰的修建，從天文觀測到精密儀器的制造……人們都離不開對幾何圖形的測量、設計和計算。

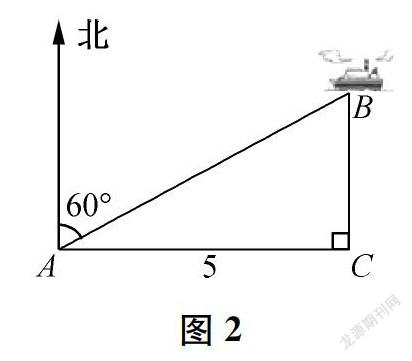
情境1小李騎車在長江邊A處游玩，發現在他所在位置北偏東60°的B處，有一艘采沙船在江中作業。當他向正東方向騎行5千米到達C處后，發現該采沙船在他的正北方向（如圖2）。

問題1你能就此情境提出一個數學問題嗎？

情境2小李騎車在長江邊A處游玩，發現在他所在位置北偏東60°的B處，有一艘采沙船在江中作業。當他向正東方向騎行5千米到達C處后，發現該采沙船在他的北偏西45°方向（如圖3）。

問題2你能結合情境1的研究經驗，提出一個數學問題，并研究一般結論嗎？

設計意圖：數學源于生活，依托一些生活實際問題，讓學生用數學的眼光去觀察、用數學的思維去分析、用數學的語言去表達，培養良好的數學素養。結合情境1，讓學生主動思考、研究，培養學生發現問題、提出問題的能力。遷移情境1及問題1的基本活動經驗，進一步研究情境2和問題2，讓學生發現、提出數學問題，并探索、得出一般結論。這兩個情境、問題是后續學生活動、數學建構的基礎。

（二）學生活動，分析問題

活動1結合情境1和問題1，研究直角三角形的邊角關系。

預設問題：在△ABC中，已知∠B=30°，∠C=90°，BC=5，求AB、AC的長。

本質揭示：本題實際是研究直角三角形的邊角關系。

當△ABC是直角三角形時，假如∠C為直角，那么有sinA=ac，sinB=bc，sinC=1=cc。所以asinA=bsinB=csinC=c。

設計意圖：活動1與情境1、問題1相呼應，研究直角三角形的邊角關系，為推廣研究一般三角形的邊角關系做好準備。

活動2結合情境2和問題2，探索一般三角形的邊角關系。

提出猜想：三角形的各邊和它所對角的正弦之比相等，即asinA=bsinB=csinC。

畫板驗證：如圖4。

推理論證：對于以上猜想，你能結合以往的學習經驗，設計合適的研究方案嘗試證明這一猜想嗎？

1.方案探索。（1）轉化為直角三角形中的邊角關系（借“高”化直）;（2）建立直角坐標系，利用三角函數的定義（借“系”解形）;（3）通過外接圓，將任意三角形問題轉化為直角三角形問題（借“圓”化直）;（4）利用向量的投影或者向量的數量積產生三角函數（借“箭”得角）。

2.嚴格論證。引導學生具體實施上述預設思路。

設計意圖：在開放的活動中，引導學生經歷“提出猜想—畫板驗證—推理論證（方案探索—嚴格論證）”等環節，感悟數學的嚴謹之美，并通過一題多證的方式，感受數學的開放之美;同時，培養學生分析、解決問題的能力。其中，方案探索的過程是喚醒并遷移已有活動經驗的較高層次能力的表現。

（三）意義建構，感知數學

在學生活動的基礎上，讓學生規范表述正弦定理，理解正弦定理的文字語言、符號語言及常見變式（見上文圖1）。

（四）數學運用，解決問題

例1小李騎車在長江邊A處游玩，發現在他所在位置北偏東60°的B處，有一艘采沙船在江中作業。當他向正東方向騎行5千米到達C處后，發現該采沙船在他的北偏西45°方向。求 AB、AC的長。

說明一般地，我們把三角形的三個角和它的對邊分別叫作三角形的元素。已知三角形的幾個元素求其他元素的過程叫作解三角形。

例2根據下列條件解三角形。

（1）a=1，A=30°，B=45°;

（2）a=1，b=2，B=45°。

結論利用正弦定理可以解決的問題：（1）已知兩邊及其一條邊的對角，求其他元素;（2）已知兩角和一邊，求其他元素。

練習請在橫線上添加適當條件，并讓同桌解答。

根據下列條件，解三角形。

設計意圖：例1與情境2相呼應，即學即用，激發學生的學習興趣。例2一方面幫助學生鞏固所學，另一方面讓學生及時總結，加深對正弦定理的認識，同時培養學生提出問題和解決問題的能力。

（五）回顧反思，理解數學

通過梳理重構，幫助學生整體建構知識結構（見上文圖1）;通過對化歸、分類討論、數形結合等數學思想方法的感悟，讓學生回歸本真、理解數學;通過“你還能找到正弦定理的其他證明方法嗎？”的拓展反思，將課堂延伸至課外，為培養學生的創新思維創設機會和平臺。

（六）課外作業，鞏固數學

必做題教材第9頁練習1、2、3。

選做題在△ABC中，a=1，b=2，A=30°， 求B。

探究題嘗試利用多種方法證明正弦定理。

三、教學反思

（一）活動經驗是在學習過程中積累的

在數學教學中，數學活動的一個主要目的是讓學生經歷探究的過程、思考的過程、抽象的過程、預測的過程、推理的過程及反思的過程等，獲取豐富的過程性知識，最終形成應用數學的意識。對于本節課，正弦定理的結論固然重要，但發現并證明定理的過程更加重要。學生在參與正弦定理發現、證明、應用的過程中所形成的感性知識、情緒體驗和應用意識、創新意識等，即為數學活動經驗。強調基本活動經驗即強調數學學習過程。

（二）問題的提出與解決依托于活動經驗的遷移

“發現問題—提出問題—分析問題—解決問題”是一個整體。問題發現、提出以后需要分析、解決，而在分析、解決的過程中又會不斷地發現、提出新的問題。這種螺旋上升促進了研究的不斷深入。作為教師，我們要在發現問題、提出問題中培養學生的“問題意識”。而這種意識則離不開已有經驗的遷移作用。在正弦定理的學習過程中，問題的提出始終伴隨著經驗的遷移：在合適的情境中，遷移解直角三角形的經驗，發現并提出問題;在得出猜想的基礎上，依托以往的學習經驗，提出研究方案，并嘗試證明正弦定理。而在新問題的解決過程中，學生的學習經驗又不斷得以豐富、完善。

*本文系江蘇省教育科學“十三五”規劃重點資助項目“基于大數據分析的數學學習研究”（編號：Ba/2016/02/6）的階段性研究成果。

參考文獻：

[1] 范東暉.積累基本活動經驗 發展數學核心素養[J].數學通報，2018（9）.

[2]張筱瑜，汪曉勤.“正弦定理”：用歷史拓思維、潤情感[J].教育研究與評論（中學教育教學），2015（6）.

[3]王新民，王富英，王亞雄.數學“四基”中“基本活動經驗”的認識與思考[J].數學教育學報，2008（3）.

[4]曾榮.發現問題：一種創造性的思維活動[J].江蘇教育，2018（9）.