開發數學應用問題課程資源的實踐探究

孔傳輝

培養學生數學應用意識是數學教學核心目標之一，開發數學應用問題的課程資源有助于培養思維能力，增強學生對數學的理解和應用意識，從而實現數學價值，有效培養學生數學素養.但許多教師開發課程資源的意識比較淡薄，過分依賴教材“供給制”，使學習資源缺少靈活性.因此開發數學應用問題課程資源是數學教學十分有研究價值的課題.

一、巧用教材

1.緊扣變化，結合時代

教材雖然提供了較為豐富的常規應用題，但已滿足不了學生需求，教師要與時俱進地對教材的常規應用題進行創新，以激發學生學習興趣.改編時可賦予題目新時代背景下的文字氣息、改變設問方式、變換題設條件、互換條件結論，或者拓展類比成新的數學建模應用問題.

【案例1】 甲乙兩地相距250km，某天小穎從上午7：50由甲地開車前往乙地.在上午9：00、10：00、11：00這三個時刻，車上的導航儀都進行了相同的提示：如果按出發到現在的平均速度繼續行駛，那么還有1個小時到達乙地.如果導航儀的提示語都是正確的，那么在上午11：00時，小穎距乙地還有 ? ? ? km.

【評析】本題是一道常見傳統行程應用題，看似不起眼，但加入車和導航儀這個新時代背景下的文字，整個題就鮮活起來，契合時代特點，一下子就把學生的興趣調動起來，這是一種很好的對數學常規應用題進行加工再創造的方法.

2.順應背景，契合實際

純數學問題需要創造相應的背景，放在實際的環境中去解決，按照科學性、現實性、新穎性、趣味性和可行性的原則，創設學生熟知的生活背景，根據實際情況設計有一定應用價值的應用問題，有助于豐富和延伸純數學問題的內涵和應用價值.

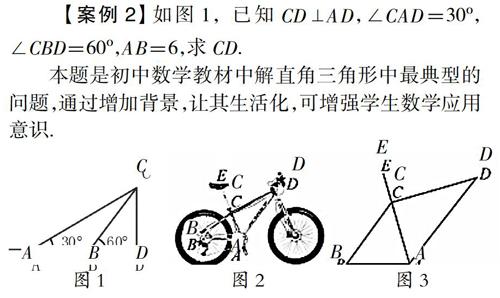
【案例2】 如圖1，已知CD⊥AD，∠CAD=30？紫，∠CBD=60？紫，AB=6，求CD.

本題是初中數學教材中解直角三角形中最典型的問題，通過增加背景，讓其生活化，可增強學生數學應用意識.

背景：學校倡導“低碳生活”，鼓勵學生以自行車作為代步工具.如圖2所示是學生小沈的自行車的實物圖.車架檔AC與CD的長分別為45cm，60cm，且它們互相垂直，座桿CE的長為20cm，點A，C，E在同一條直線上，且∠CAB=60？紫，如圖3.

（1）求車架檔AD的長;

（2）求車座點E到車架檔AB的距離.

【評析】本題引入了環保熱點問題，情境設置自然，貼近學生的生活，設計有現實性、趣味性、話題性，不僅能使學生感受到數學學習樂趣，并且能讓學生關注生活中的數學問題，體會數學的應用價值.

二、借助環境

1.校園為本

教師要關注校園生活，善于發現校園中的數學資源，為開發應用問題作資源支撐.例如：上課時間與注意力最佳問題、長跑時心率與極限問題、投擲實心球角度問題、校園內不爬高測旗桿高問題、教室采光問題，等等.

【案例3】 學校即將開運動會，但是學校跳遠場地的沙坑前段時間被雨水沖出了一個“圓錐形坑”.數學老師要求數學課外活動小組的同學去解決沙坑的填埋問題，同學們于是帶著皮尺去測量這個“圓錐形坑”的深度，圖4所示是同學們選擇測量方案：

①先測出沙坑坑沿的圓周長是10.54m;

②甲同學直立于沙坑坑沿的圓周所在的平面上，經過適當調整自己所處的位置，當位于B時恰好視線經過沙坑坑沿圓周上一點A看到坑底S（甲同學的視線起點C與點A，S三點共線），經測量：AB=1.2m，BC=1.6m.

根據以上測量數據，求“圓錐形坑”的深度（圓錐的高）.

【解析】取圓錐底面圓心O，連結OS，OA，

則∠O=∠ABC=90？紫，OS∥BC，

∴∠ACB=∠ASO，

∴△SOA∽△CBA，

∴=，∴OS=

∵OA=≈1.68，BC=1.6，AB=1.2，

∴OS≈2.3，

∴“圓錐形坑”的深度約為2.3m.

【評析】此題是關注校園生活，提煉數學資源，解決實際問題的典例.這樣的設計形式搭建了生活資源的載體，有助于引導學生充分提煉學習資源，豐富學習內容和方式.

2.探尋家庭

生活中處處充滿著數學，家庭生活是學習數學的起源，教師要引導學生以觀察、調查、實踐等形式主動收集應用數學的信息，捕捉家庭生活中的數學問題或數學現象，開發自主學習能力.

【案例4】在十一黃金周期間，小王和爸爸媽媽去安吉大峽谷漂流，在售票大廳看到表（一）和表（二），小明思考了一下，對爸爸說：“若漂流船在靜水中的速度不變，那么我能算出它的速度和水流速度.”爸爸說：“你真聰明！”你知道小明是如何求出的嗎？請你試著求漂流船在靜水中的速度和水流速度.

【評析】這道題通過對現實生活中的事件進行“素材”編擬，呈現的信息是開放的，但并非所有信息都是有效，需要進行合理的取舍，這類問題能激發學生解決問題的內在動力，獲得真實的內心體驗，感受數學無處不在.

三、綜合拓展

1.有效改編

經典試題一直是數學應用的資源平臺，許多中考試題、pisa測試題都可以用來作為開發數學應用問題課程的素材.Pisa類測試可強化對學生知識面、綜合分析、創新素養等方面的培養，教師在教學中要充分利用這些素材提高學生的數學能力.

【案例5】已知A地在B地的西方，且有一以A、B兩地為端點的東西向直線道路，其全長為400公里.今在此道路上距離A地12公里處設置第一個廣告牌，之后每往東27公里就設置一個廣告牌，如圖5所示.若某車從此道路上距離A地19公里處出發，往東直行320公里后才停止，則此車在停止前經過的最后一個廣告牌距離A地多少公里？（ ? ）

A.309 ? ? B.316 ? ? C.336 ? ? ?D.339

【解析】設此車停止時前面有x個廣告牌，根據題意得12+27（x-1）≤320+19，x≤13，即此車停止時前面有13個廣告牌，并且超過第13個廣告牌3公里，所以此車在停止前經過的最后一個廣告牌距離A地320+19-3=336公里.故選C.

【評析】這道經典習題背景直觀、學生熟悉，通過改編設計，幫助學生利用不等式的數學模型，進行可行性研究，讓學生感受到數學模型的重要性，提高學生的建模能力.

2.學科整合

數學與其他學科之間有較多聯系，教師要試著以不同的學科知識為背景，或以相關學科知識為載體來設計問題，充分體現數學與其他學科間的整合，讓學生從不同的方向和角度感受數學知識的產生與變化、發展與應用的過程，拓展學科知識視野，提高綜合能力.

【案例6】桌面上有甲、乙、丙三個圓柱形的杯子，杯深均為15公分，各裝有10公分高的水，且表（三）記錄了甲、乙、丙三個杯子的底面積.今小明將甲、乙兩杯內一些水倒入丙杯，過程中水沒溢出，使得甲、乙、丙三杯內水的高度比變為3∶4∶5.若不計杯子厚度，則甲杯內水的高度變為 ? ? ? ? 公分.

A.5.4 ? ? ?B.5.7 ? ? ?C.7.2 ? ? ?D.7.5

【評析】這一問題融合了數學中的比、方程思想、科學實驗與體積變化等知識，使學生充分利用學科知識之間的聯系來解決實際問題.學科的有效整合、綜合運用讓學生找到應用數學的廣闊途徑，從而呈現數學的豐富內涵，突出了數學作為工具學科的本質.

總之，教師在數學教學中要針對不同層次學生因材施教，開發不同層次的數學應用問題，遵循“科學性、客觀性、適切性、時代性、探索性、開放性、動態性”等原則，處理好“生活化”與“數學化”的關系，多渠道、多角度、全方位拓寬數學應用問題的課程資源，較好地提升學生數學素養.